ここでは練習問題を通して、関数とは何か、座標、変域、比例の表し方の基本を学んでいきます。中学数学の中でも重要度の高い分野なので、基本的な事柄を理屈から理解するようにしていきましょう。
関数とは何か、座標、変域、比例の表し方を理屈から理解したい人は以下のページを参考にしながら進めてください。
関数であるもの
与えられた文章から式を作れるかどうかがポイントになります。何が関数となるのかをおさえましょう。
練習1 次のうち$y$が$x$の関数であるものを選べ。
㋐ 1個100円のチョコを$x$個買った時の代金$y$円
㋑ 晴れた日の最高気温$x$℃と最低気温$y$℃
㋒ 1辺が$x$㎝の正方形の面積$y$㎠
㋓ $x$m歩いたときの歩数$y$歩
㋔ 縦が$x$㎝の長方形の面積$y$㎠
【考え方】
関数とは$x$の値を1つ決めると、それに伴い$y$の値も1つに定まる関係です。
【解答】 ㋐ ㋒
【補足】
㋑ 最高気温を1つ決めたからといって最低気温が決まるなんてことはありません。よって関数とはいえません。
㋒ 一歩あたりの長さがわかっていれば歩数と距離の間に関数が成り立ちますが、ここでは特に一歩あたりの条件が何もないので関数とはいえません。
㋔ 横の長さもわからないと長方形の面積は求まらないので、関数とはいえません。「縦が$x$㎝、横が10㎝の長方形の面積$y$㎠」という様に、横の長さが与えられている場合は関数といえます。
座標の表し方
慣れればどうってことない内容ですが、学んだばかりの頃は何かと勘違いしやすい部分です。
座標の表し方をここで覚えておきましょう。
練習2 次の図で、点A~Eの座標を答えよ。
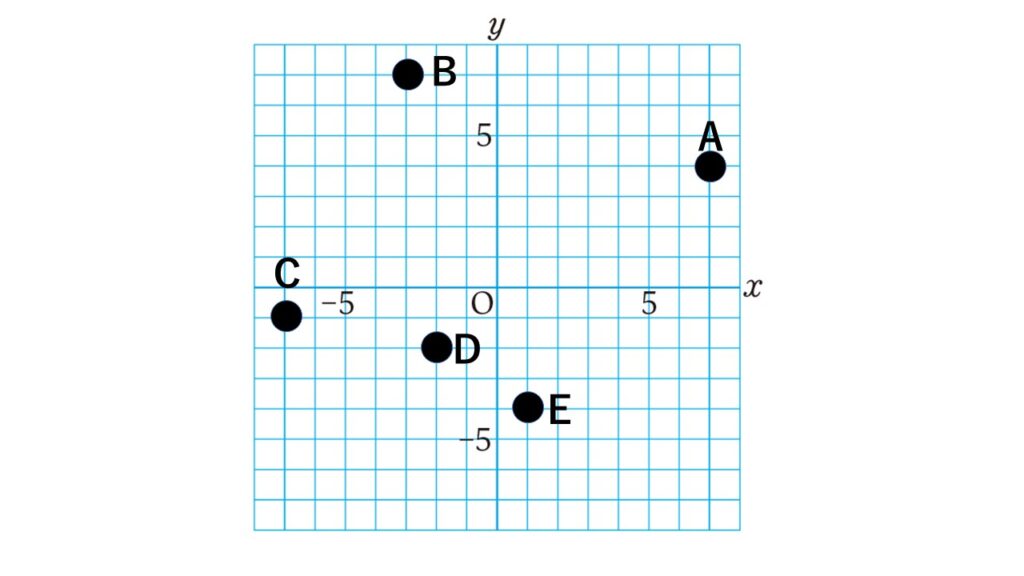
【解答】
A$(7,4)$ B$(-3,7)$ C$(-7,-1)$ D$(-2,-2)$ E$(1,-4)$
【補足】
座標を表すときは、$x$座標と$y$座標の間に必ず $,$ を入れます。
単にスペースを入れただけでは座標を表したことにならないので要注意です。
A$(7 4)$ ←これでは座標といえない。
変域の表し方
以上、以下、より大きい、未満。それぞれの使い分けをしっかり覚えておきましょう。
練習3 $x$の変域を不等号を使って表せ。
(1)$x$の変域が8以下である
(2)$x$の変域が5以上である
(3)$x$の変域が10未満である
(4)$x$の変域が$-$4より大きい
(5)$x$の変域が$-$8以上3以下である
(6)$x$の変域が$-$8より大きく3より小さい
(7)$x$の変域が0より大きく7以下
【解答】
(1)$x≦8$ (2)$x≧5$ (3)$x<10$
(4)$x>-4$ (5)$-8≦x≦3$
(6)$-8<x<3$ (7)$0<x≦7$
【補足】
以上 以下 とあったらその値を含めて考えます。
8以上とあったら8を含めて大きい値を指します。
$y$を$x$の式で表す
「$y$を$x$の式で表せ」といった出題は、数学の定番中の定番です。
解き方、答え方を理解してください。
練習4 $y$は$x$に比例し$x=5$のとき$y=15$である。
(1)$y$を$x$の式で表せ。また、比例定数を答えよ。
(2)$x=15$のときの$y$の値を求めよ。
【考え方】
「$y$は$x$に比例し・・・」とあったら、$y=ax$の形を思い出す。
(1)問題文に「$y$を$x$の式で表せ」とあったら、どんな問題でも答え方は $y=〇x$ の形で答える
(2)(1)で出た式をもとに考える
【解答】
(1) $y=ax$
$x=5$、$y=15$より
$15=5a$
$5a=15$
$a=3$
よって $y=3x$ 比例定数 $3$
(2) $y=3x$ に $x=3$ を代入
$y=3\times3$
$y=15$
練習5 $y$は$x$に比例し$x=-6$のとき$y=8$である。
(1)$y$を$x$の式で表せ。
(2)$x=12$のときの$y$の値を求めよ。
【考え方】
$x$の値が負でも解き方は同じです。
【解答】
(1) $y=ax$
$x=-6$、$y=8$より
$8=-6a$
$-6a=8$
$6a=-8$
$a=-\dfrac{8}{6}$
$a=-\dfrac{4}{3}$
よって $y=-\dfrac{4}{3}x$
(2) $y=-\dfrac{4}{3}x$ に $x=12$ を代入
$y=-\dfrac{4}{3}\times12$
$y=-4\times4$
$y=-16$
練習6 $y$は$x$に比例し、$x$と$y$の関係は表のようになる。
このとき、次の問いに答えよ。
(1) $y$を$x$の式で表せ。
(2) ㋐、㋑に当てはまる数を求めよ。

【考え方】
練習6は、練習4や練習5と全く同じ内容です。問題が言葉で示されているか、表で示されているかの違いだけです。
(1)表から$x$が$1$のとき$y$が$4$とわかります。
(2)(1)で求めた式を使い、$x$が$3$のときの$y$の値、$y$が$56$のときの$x$の値をそれぞれ求めます。
【解答】
(1) $y=ax$
$x$が$1$のとき$y$が$4$なので
$4=a\times1$
$a=4$
よって求める比例の式は
$y=4x$
(2)$y=4x$ で表より
㋐ $x=3$を代入して$y$の値を求めれば良いから
$y=4\times3$
$y=12$
㋑ $y=56$を代入して$x$の値を求めれば良いから
$56=4x$
$4x=56$
$x=14$
練習7 次の関係について、$y$を$x$の式で表せ。また比例定数を答えよ。
(1)1冊165円のノートを$x$冊買ったときの代金$y$円。
(2)時速45㎞で走る自動車が$x$時間走り続けたときの移動距離$y$㎞。
(3)水そうに毎分7ℓずつ水を入れるときの、$x$分後の水の量$y$ℓ。
(4)底辺10㎝、高さ$x$㎝の三角形の面積$y$㎠。
(5)3mの重さが180gの針金で、$x$mのときの重さ$y$g。
【考え方】
具体的な事柄で出題されていても「$y$を$x$の式で表せ」とあるので、答え方は $y=〇x$ の形です。
問題文から何が$x$で何が$y$なのかを読み取ります。
【解答】
(1)$y=165x$ 比例定数165
(2)$y=45x$ 比例定数45
(3)$y=7x$ 比例定数7
(4)$y=5x$ 比例定数5
(5)$y=60x$ 比例定数60
【補足】
$x$が1のときなら式を作りやすいと思います。
(1)なら1冊の値段165に買った冊数をかければ式を作れます。
(2)なら1時間で進む距離45に走った時間をかければ式を作れます。
(3)なら1分あたりの水の量7に時間をかければ式を作れます。
このように$x=1$のときが、比例を考える時の目安になってきます。
(1)~(3)は$x=1$のときがわかりやすいですが、(4)と(5)はひとひねりあります。そしてここが注意点!!
(4)は三角形の面積を求める式を実際に書いてみます。
三角形の面積=底辺$\times$高さ$\times\dfrac{1}{2}$なので
$y=10\times$$x$$\times\dfrac{1}{2}$ より約分して
$y=5x$ となります。
問題文の10につられてそのまま10を比例定数としてしまうと誤答になってしまいます。
(5)は$x=1$、つまり1mのときの針金の重さをいったん求めておかないと比例定数を導けません。
180につられてそのまま$y=180x$としてしまうと誤答です。
繰り返しますが、$x=1$のときが比例を考える時の目安なので、$x=1$のときの$y$の値を常に考えるようにしましょう。そしてその値が比例定数となります。




