分配法則の基本を確認しよう

分配法則の意味

分配法則とは、（かっこ）がついた式を（かっこ）を外した式に変形することをいいます。
左辺と右辺で計算式の見た目は違うけど計算結果は同じになる、というもの。

$a(b+c)=ab+ac$

まずこの形をしっかり覚えましょう。

$a(b+c)$　は
$ab+ac$　と変形できます。

本当に同じ計算結果になるのかを、$a=4,b=2,c=1$　として実際に確かめてみます。

左辺、右辺ともに$12$で等しいですね。

分配法則は文字式の計算でよく使います。

●分配法則の意味をイラストで確かめる●

例）4つの袋にそれぞれ飴が2個ずつ入っています。それぞれの袋にもう1個ずつ飴を追加します。
全部で飴は何個になりますか？

状況はイラストの様になります。

～$a(b+c)$　の考え方～
この考え方は、
1つの袋について飴の数量を注目し、それが4袋分ある
というものです。
$4\times(2+1)$
つまり$4\times3$となり$12$個となります。

～$ab+ac$　の考え方～
この考え方は、
元々袋にあった飴の数と追加する飴の数を別々に数えている
というものです。
$4\times2$と$4\times1$を別々にし
最後に足して飴の数を出しています。

このようにして考えると、
$a(b+c)$　と　$ab+ac$　は
見た目や考え方は違うものの、計算上は全く同じ結果になることがわかります。

改めて書きますが、

$a(b+c)=ab+ac$

この形をしっかり覚えましょう。

分配法則の計算方法

分配法則は（かっこ）を外す操作のことです。
なのでテストなどの問題で「分配法則を使って計算せよ」とあったら、（かっこ）を外す計算をします。

（かっこ）の外にある数を、（かっこ）の中にある数それぞれにかけて外します。
例題を使って説明します。

問題1）　$a(b+c)$　を計算しなさい。
考え方）$a$を$b$にかけ算する。また、$a$を$+c$にもかけ算する。

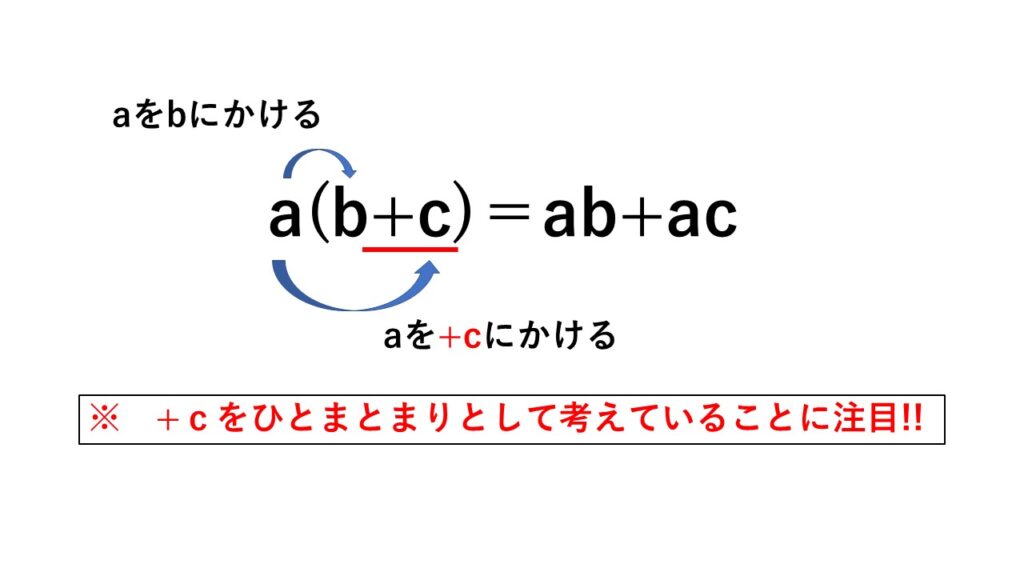
このとき、数字の左隣にある符号をひとまとまりとして計算します。
なので$+c$にかけ算します。

問題2）　$a(b-c)$を計算しなさい。
考え方）$a$を$b$にかけ算する。また、$a$を$-c$にもかけ算する。

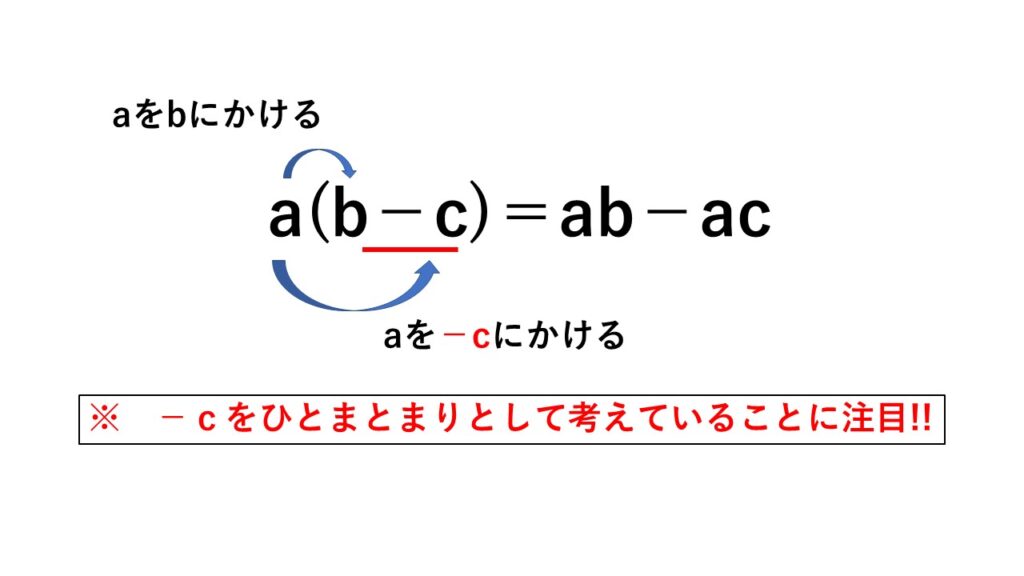
繰り返しますが、数字の左隣にある符号をひとまとめとして考えます。

問題3）　$-a(b+c)$を計算しなさい。
考え方）数字の左隣にある符号をひとまとまりとするから、$-a$をそれぞれにかける。

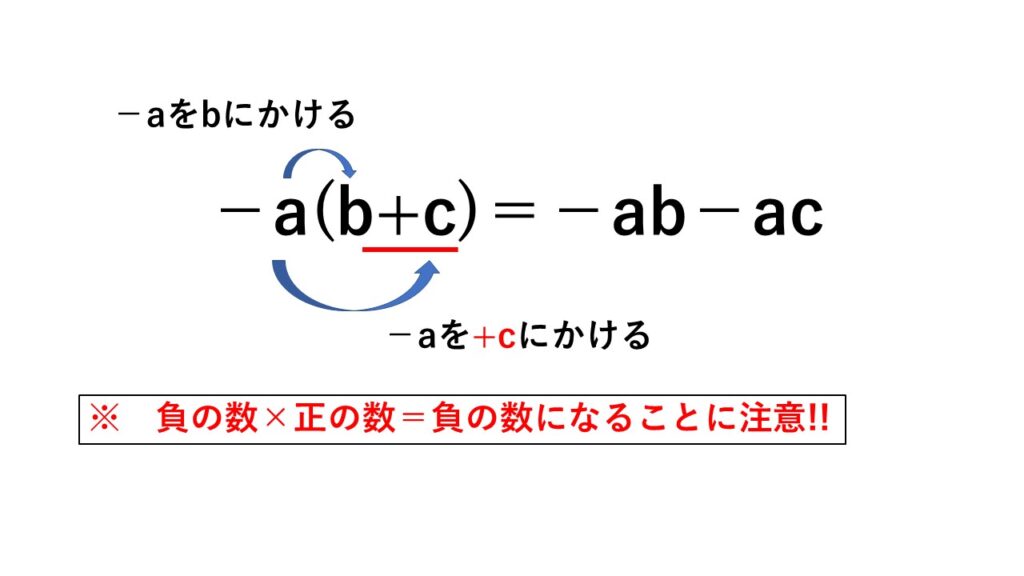
問題4）　$-a(-b-c)$を計算しなさい。
考え方）数字の左隣にある符号をひとまとまりとするから、$-a$をそれぞれにかける。

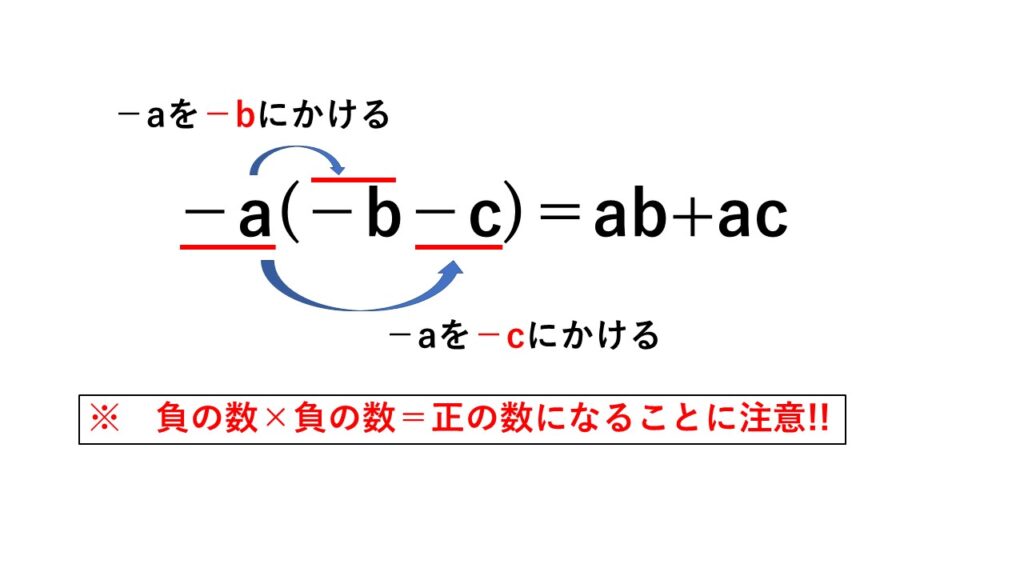
大事なことなので繰り返しますが、（かっこ）を外す計算が分配法則です。
数字の左隣にある符号をひとまとめにしてかけ算を進めます。

参考）　$a(b-c+d)$を計算しなさい。
考え方）（かっこ）の中にいくつ数字があってもやり方は同じです。
$a(b-c+d)=ab-ac+ad$　となります。

（かっこ）の中の数それぞれにかけ算する