座標の考え方　表し方

座標の基本をマスターする

座標とは
数値の組を使って点の位置を明確に示す方法
のことを言います。

点の位置（場所）を知りたいから座標を使うと思ってください。

例えば、待ち合わせの場所を教える時に
「ここだよ、ここ」と伝えたところで、
聞かされた側は
「どこだよ!!」となります。
何かしらの基準を示したうえで伝えないと相手はわかりません。
そのために住所を使って伝えたりしますよね。
今日は渋谷で5時、みたいな感じで。
場所をはっきり示さないとお互い別の場所に行ってしまい、違う違うそうじゃそうじゃないとなってしまいます。

数学の世界でも同じです。
場所を示すときに
「ここだよ、ここ」と伝えてもわかりません。
そのために数学の世界でいう住所のようなものを使って場所を示します。
それが座標というわけです。

座標の表し方

座標は「横方向」「縦方向」と2つの方向で考え、横方向は$x$、縦方向は$y$で表します。
（奥行に関しても考えますが、中学では学ばないのでここでは割愛します）

そのとき$x$軸や$y$軸というものを使って表します。
軸とは数直線のようなものと覚えておくと良いでしょう。
図を使って説明します。

横方向を$x$軸
図1は$x=4$を表しています。
もう少し詳しく言うと、
「点は$x$軸上の$x=4$の位置にある」
ということになります。

図2も$x=4$を表しています。
ただ図1では点は$x$軸上（$x$軸に重なっているという意味）にありましたが、図2では縦方向に移動した位置にあります。
少し違和感があるかもしれませんが、これでも$x=4$と解釈します。

冒頭で、「点の位置（場所）を知りたいから座標を使う」と書きました。
図1や図2では$x$軸を使うことで、横方向の位置についてははっきりわかりました。
でも縦方向については$x$軸だけで表そうとしても上手く表現できません。
そこで縦方向について$y$軸を使って同じように考えていきます。

$y$軸を使うことで、縦方向の位置についてははっきりわかりました。
すると、$x$軸と$y$軸を組み合わせることで横方向と縦方向の両方の位置を同時に表せますね。
ということで、図2と図4を合わせたものが次の図5です。

$x$軸と$y$軸を0の所で合わせます。
これにより横方向と縦方向を同時に表すことができました。

図5は$x=4$で$y=3$の点を表しています。
このことを
$(4，3)$と表します。

$(x$座標 , $y$座標$)$の順で書きます。
この表し方をしっかり覚えておきましょう。

ここまでのまとめ

ここまで初めて聞くことばも多かったと思うので、重要用語も含めて簡単にまとめておきます。

• 座標　数値の組を使って点の位置を明確に示す方法
• $x$座標　横方向の点の位置
• $y$座標　縦方向の点の位置
• 原点　$x$座標も$y$座標も0の点
• 軸　　数直線のようなもの
• $x$軸　横方向の位置を表す数直線
• $y$軸　縦方向の方向を表す数直線
• 座標軸　$x$軸と$y$軸を合わせた言い方

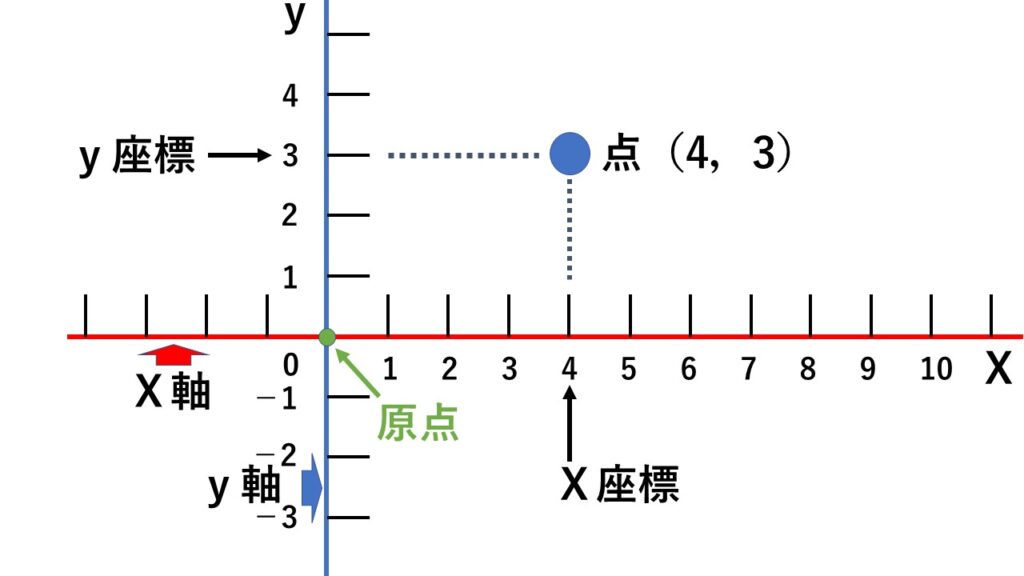
「これから点の座標を表しますよ」ってことで、
$(x,y)=(4,3)$という書き方もしますので、合わせて覚えておきましょう。

また、座標は必ず数値の組を使って表します。
だから、「座標を答えなさい」との問いに対して、単に数値1つだけを答えたとしてもそれは答えになりません。

それでは次の練習問題を使って座標の表し方を確認しておきましょう。

練習1
図の（1）～（5）の座標をそれぞれ答えよ。

解答
（1）$(5,7)$　（2）$(7,-1)$　（3）$(0,0)$　（4）$(-3,1)$　（5）$(-5,-5)$

$x$軸や$y$軸に関して対称な点の座標

座標の基本を学んだので、次に$x$軸に関して対称な点の座標や$y$軸に関して対称な点の座標について練習していきます。

練習2
（1）点$( 4, 7 )$について$x$軸に関して対称な点と、$y$軸に関して対称な点の座標を求めよ。

（2）点$(-6,-2)$について$x$軸に関して対称な点と、$y$軸に関して対称な点の座標を求めよ。

考え方
$x$軸に関して対称な点とは、$x$軸で折り曲げた時にピタリと重なる位置のことです。
同様に$y$軸に関して対称な点とは、$y$軸で折り曲げた時にピタリと重なる位置です。
座標の目盛りを参考に見ていきましょう。

解答

$x$軸に関して対称な点の座標は、$x$座標の数値はそのままで、$y$座標の数値は符号が逆になります。
$y$軸に関して対称な点の座標は、$x$座標の数値は符号が逆になり、$y$座標の数値はそのままになります。

原点に関して対称な点の座標

最後に原点に対して対称な点の座標を考えてみます。
原点に関して対称な点とか、原点に対して対称な点、原点について対称な点などといいますが、どれも同じ意味です。
要は、ある点の座標を、原点を中心に180°回転させたときに移る点の座標のことを表しています。
点対称を考えていけば良いということになります。

それでは次の練習問題を使って理解していきましょう。

練習3
点$(4,7)$の原点に関して対称な点の座標を求めよ。

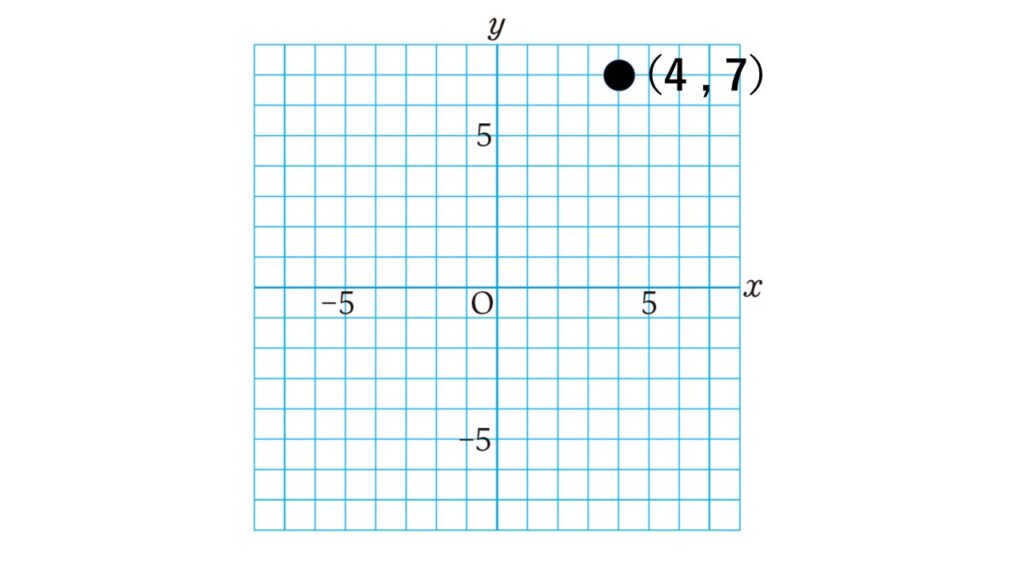
考え方
原点を中心に180°回転させた点対称な図形を考えていけば求められます。

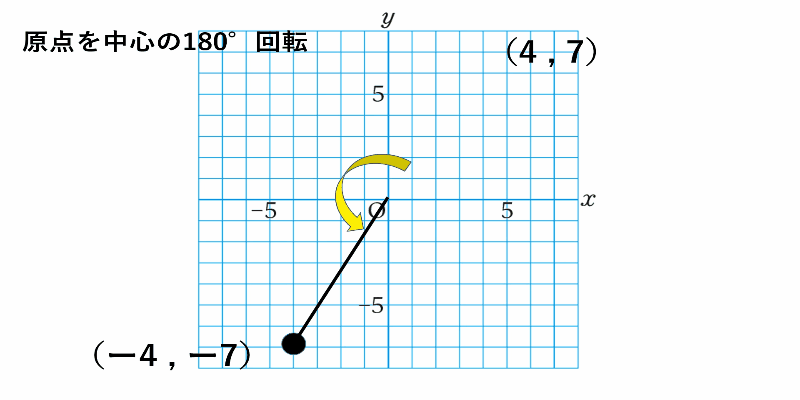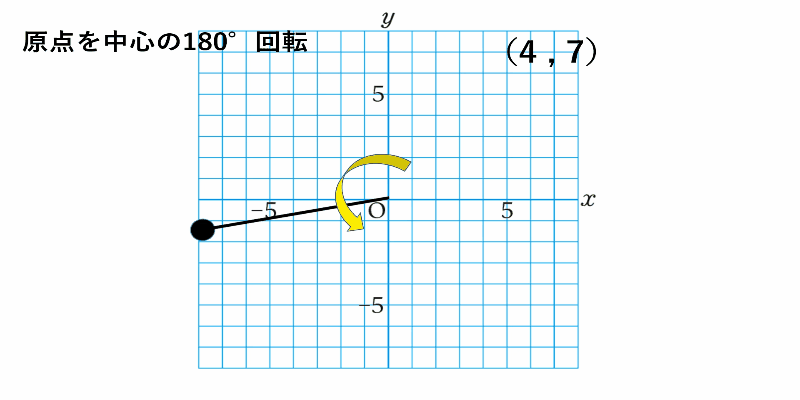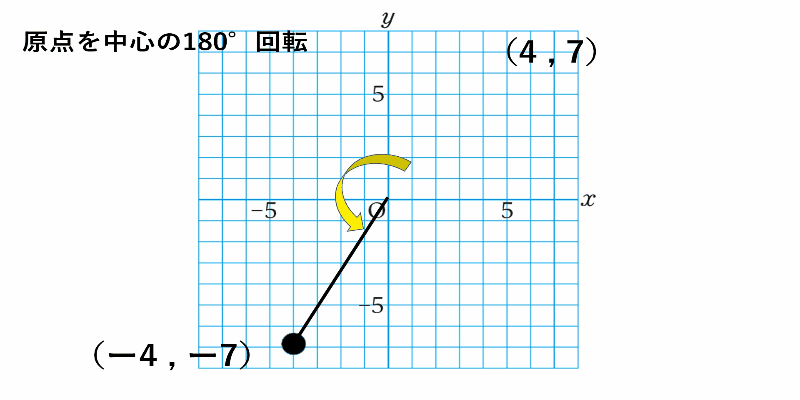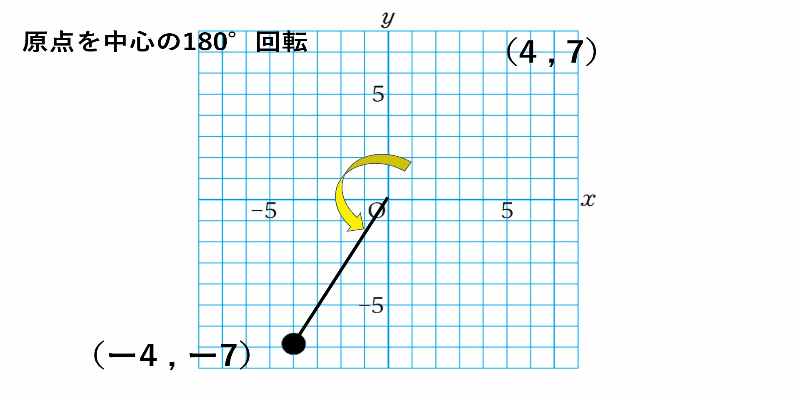
解答　$(-4,-7)$

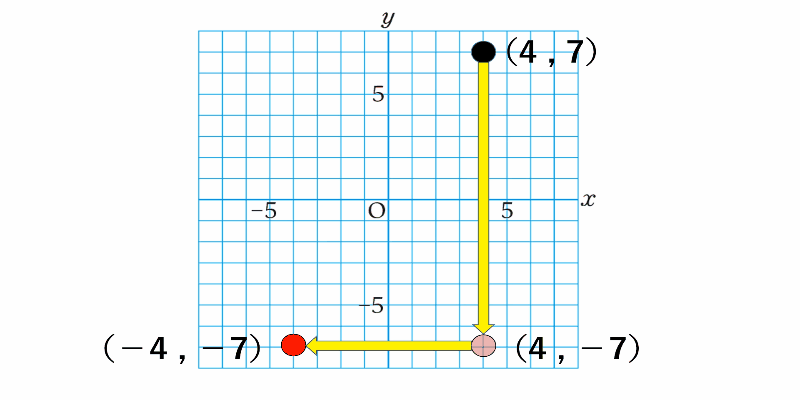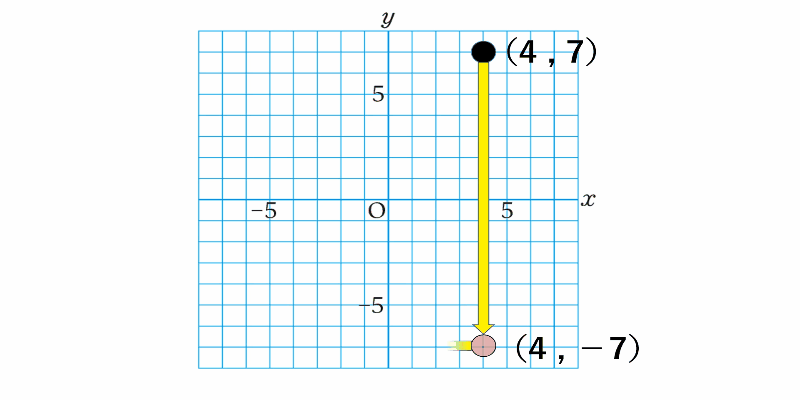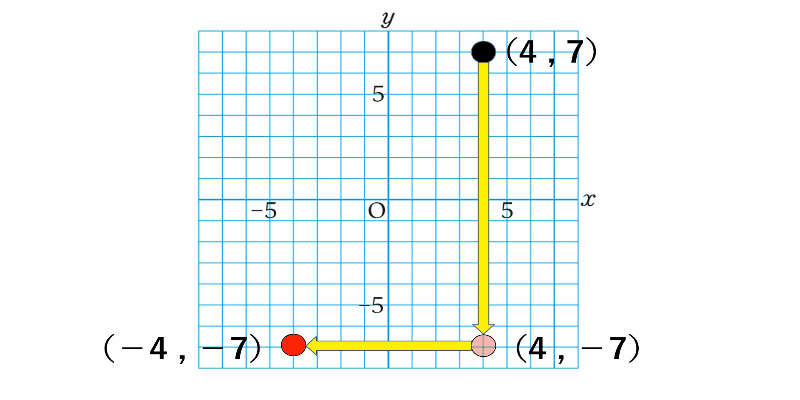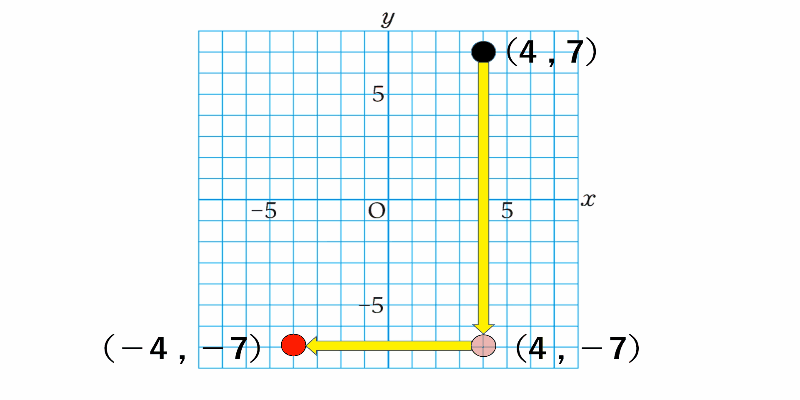
座標平面上の点を原点中心に180°回転させると
$x$座標、$y$座標ともに元の点の座標と符号が逆になる

180°回転といってイメージが湧かない場合は、
元の点を一度$x$軸に関して対称な点を考え、
そこからさらに$y$軸に関して対称な点を考えると良いでしょう。