放物線のグラフと変域

関数$y=ax^2$の変域を使った応用問題は、中学3年生なら誰でも必ず1度は同じところで間違えます。
なぜなら$\:y\:$の値が減ったり増えたりするから。
ということでここでは、関数$y=ax^2$の変域問題の間違えやすいところを解説していきます。

なお変域の基本の考え方はこちらのページで確認できます。
変域の表し方に不安のある人は必ずこちらを復習してから次に進んでください。

関数$y=3x^2\:$の変域

実際に問題を解いてみましょう。

基本例題1
関数$y=3x^2\:$について、$x$の変域が$-1\leqq x\leqq2$のときの$\:y\:$の変域を求めよ。

考え方
$y$の変域とは$y$の値の取りうる値の範囲のこと。つまり
$x$の値が$-1$から進み始め$2$に到着するとき、それに伴い$y$の値はどの値を取るかを求めます。
$y=ax^2$の性質に慣れるまでは、必ずグラフをかいて変域を考えるようにしましょう。

よくある間違った解答
$x=-1\;$のとき$y=3\times(-1)^2=3$
$x=\:2\quad$のとき$y=3\times2^2=12$
よって$\quad 3\leqq y \leqq12$　（誤答）
グラフをかかずに解答するとこのような誤答をする危険があります。

解答

$x=-1\;$のとき$y=3\times(-1)^2=3$
$x=\:2\quad$のとき$y=3\times2^2=12$
よって$\quad0\leqq y\leqq 12$

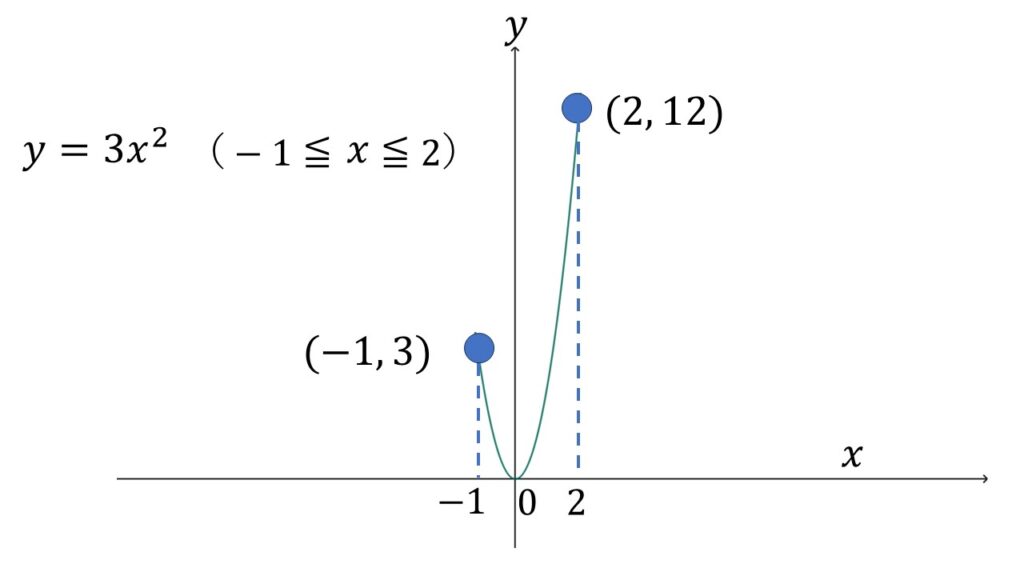
解説
なぜ$y$の最小値が$0$となるのかは、グラフをかいて考えれば一目瞭然です。
$x=-1$のとき$y=3$、つまり$y$の変域は$y=3$からスタートします。
$x$の値が増えていくごとに、$y$の値は小さくなっていきます。
そして$x=0$となったとき、$y=0$となります。

$x=0$を境にさらに$x$の値が増えていくと、今度は$y$の値は大きくなっていきます。
$x=2$になったとき$y=12$となり、ここが変域の最終地点となります。

変域は「取り得る値の範囲」ということです。
取り得る値、つまり$y$は$3$からスタートし$0$まで小さくなったあと$12$まで増えたということで、$\:0\leqq y\leqq 12\:$となるわけです。

関数$y=ax^2$の変域を考える際は、$x$の変域に$x=0$が含まれるかどうかがポイントとなります。
変域に慣れるまでは必ずグラフをかいて考えましょう。

類題を使って理解を深めましょう。

類題
$(1)\quad$関数$y=2x^2$について、$x$の変域が$\:-4\leqq x \leqq1\:$のときの$y$の変域を求めよ。
$(2)\quad$関数$y=-2x^2$について、$x$の変域が$\:-4\leqq x \leqq1\:$のときの$y$の変域を求めよ。

解答はこのページの下段にあります。

次に、与えられた変域から関数$y=ax^2$の$a$の値を求める問題を解けるようにします。
ただそのためには、しっかり理解しておくべき事柄があります。
ということで次の事柄を理解してから基本例題2へ進みましょう。

$y=ax^2$のグラフ　$x$の絶対値と$y$の絶対値

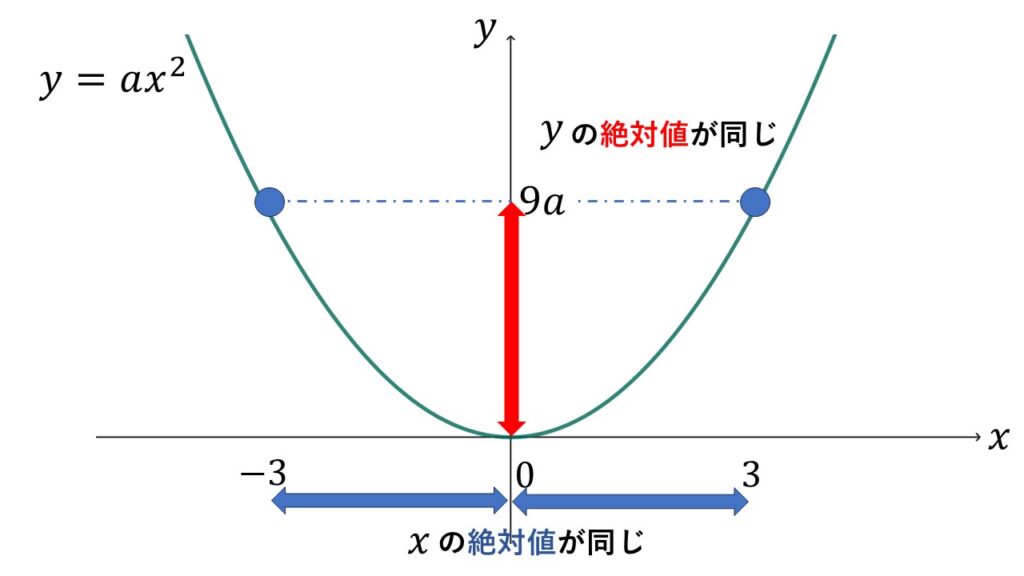
$y=ax^2$のグラフは$y$軸について線対称です。
そのため、例えば$x=-3$と$x=3$のように$x$の値の絶対値(原点からの距離のこと）が同じならば、$y$の絶対値は同じになります。

一方、$x=-1$と$x=3$のように$x$の絶対値が異なる場合、$x$の絶対値が大きい時に$y$の絶対値も大きくなります。

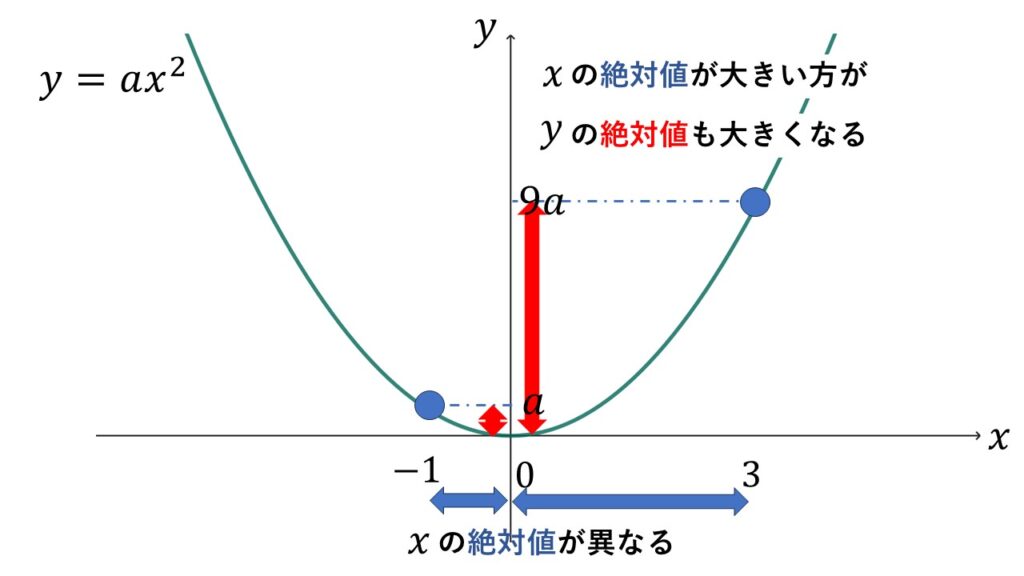
グラフをかけば一目瞭然ですが、$y=ax^2$の変域を考える際のとても重要な事柄です。
図は下に凸のグラフを挙げていますが、上に凸のグラフも同様です。
しっかり理解しておきましょう。暗記ではなく理解です。

理解してから次の例題に進みましょう。

基本例題2
関数$\:y=ax^2\:$において、$x$の変域が$-2\leqq x \leqq6$のとき$y$の変域は$0\leqq y \leqq9$となる。$a$の値を求めよ。

考え方
$x$の絶対値が大きい方が$y$の絶対値が大きくなることを利用します。
なお、$\:y\:$の変域が$0$以上なので$\:a\:$は正の値、つまりグラフは下に凸だと判断できます。

解答
$x$の絶対値が大きい方が$y$の絶対値が大きくなるので
$x=6$のとき$y=9$となる
これより
$\begin{align}9=&a\times6^2\\\\9=&36a\\\\a=&\dfrac{9}{36}\\\\a=&\dfrac{1}{4}\end{align}$

繰り返しますが、変域の問題に慣れるまではグラフをかいて考えるようにします。
グラフは上に凸か下に凸かが重要で、$a$の値が正か負かで上に凸か下に凸かが変わります。
つまり$a$の値を特定することが重要となります。
基本例題2は特にグラフをかかなくても解答できますが、グラフと変域を関連させて考えることは大切です。
必ず理屈で考えて理解するようにしましょう。

類題　補足
$(1)\:$$x=-4\:$のとき$\:y=32$
となるから
$32\leqq x \leqq0\:$とするのは誤答です。
この書き方では$32$の方が$0$より大きいことになってしまい、明らかに間違っていますよね。