関数$y=ax^2$の基本と具体例

$y$は$x$の関数で$y=ax^2$と表されるとき、$y$は$x$の2乗に比例するといいます。
何言ってるかわからないかもしれませんが、とりあえずこの表記のまま覚えてください。

$y$は$x$の2乗に比例するとは

$y$は$x$の2乗に比例する関数といえば通常$y=ax^2$を指しますが、ここは導入なので$a=1$のとき、つまり$y=x^2$で考えます。

$x$に値を代入したときの$y$の値をそれぞれ表にします。ここではいったん$x\geqq0$で考えます。

しばらく$x$と$y$との間にどんな関係があるかを確認してください。

どんな関係があるかわかりましたか？

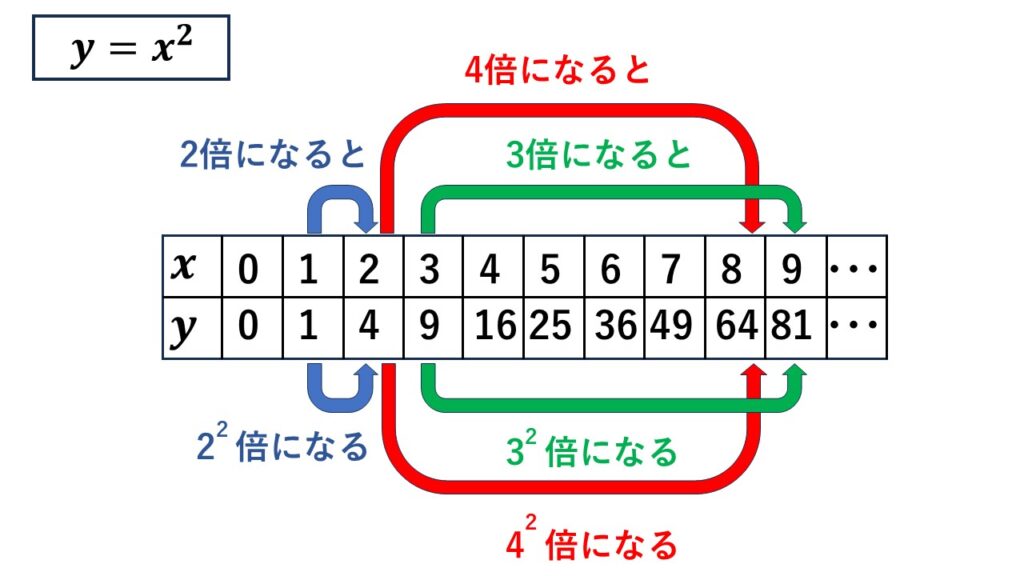
$x$が$1$から$2$に2倍になったとき、$y$は$1$から$4$と4倍となっています。
$x$が$2$から$4$に2倍になったとき、$y$は$4$から$16$と4倍になっています。
$x$が$3$から$6$に2倍になったとき、$y$は$9$から$36$と4倍になっています。

$x$が$1$から$3$に3倍になったとき、$y$は$1$から$9$と9倍となっています。
$x$が$2$から$6$に3倍になったとき、$y$は$4$から$36$と9倍となっています。
$x$が$3$から$9$に3倍になったとき、$y$は$9$から$81$と9倍となっています。

$x$が$1$から$4$に4倍になったとき、$y$は$1$から$16$と16倍となっています。
$x$が$2$から$8$に4倍になったとき、$y$は$4$から$64$と16倍となっています。

このように$y=x^2$の関係では、$x$が2倍、3倍・・・となると、それに伴い$y$の値は$x$の2乗倍になっていることがわかります。

このような関係があるときに、$y$は$x$の2乗に比例するといいます。

合わせて、
$x$が$\dfrac{1}{2}$倍になると$y$は$\dfrac{1}{4}$倍

$x$が$\dfrac{1}{3}$倍になると$y$は$\dfrac{1}{9}$倍

$x$が$\dfrac{1}{4}$倍になると$y$は$\dfrac{1}{16}$倍

となっていることもおさえておきましょう。

それでは早速$\:y=ax^2\:$がどのような形で出題されるかを超基本例題で確認しましょう。

超基本例題
$(1)\:$$y$は$x$の2乗に比例し、$x=3$のとき$y=36$となる。このとき$y$を$x$の式で表せ。また、$x=5$のときの$y$の値を求めよ。
$(2)\:$$y$は$x$の2乗に比例し、$x=-2$のとき$y=20$となる。このとき$y$を$x$の式で表せ。また、$x=2$のときの$y$の値を求めよ。

考え方
①問題文に「$y$は$x$の2乗に比例し」とあったら、とにかく$y=ax^2$とおく
②問題に$x$と$y$の条件があるのでそれぞれ代入し$a$の値を求める
③求めた$a$を$y=ax^2$に当てはめておわり

この流れで解きます。
比例・反比例や一次関数でも似たような問題を解きましたよね。
考え方はそれと同じです。

この超基本例題は問題と解き方をそのまま覚えてしまいましょう。
テストで出題されたら必ず解答できるように!!

$y$は$x$の2乗に比例する関係の具体例

$y$は$x$の2乗に比例する関係、つまり$y=ax^2$と表せる関係にはどのようなものがあるか？
主なものを挙げます。

制動距離

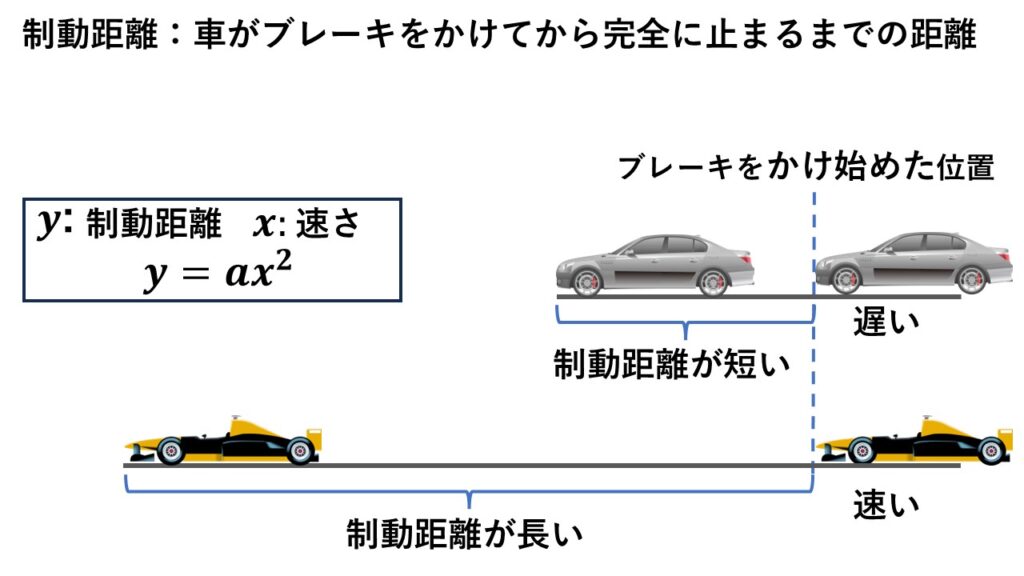
制動距離（せいどうきょり）とは、車がブレーキをかけてから完全に止まるまでに進む距離のことをいいます。

速く走る車ほど、ブレーキをかけてから完全に止まるまでに長い距離が必要だということは想像つきますよね。

制動距離を$y$、車の速さを$x$とすると、
$y=ax^2$
の関係があるそうです。

この関係式でいう$a$は、摩擦やタイヤ性能、ブレーキ性能など色々な要素を表しています。
また、同じ車でも普通に運転しているか、あるいはかっこ良いとこ見せようとドリフト走行しているかによっても$a$の値が変わってきます。

まぁ中学数学ではそこまで気にする必要はないので、制動距離の問題で$a$が出てきたら、とりあえず止まることに関連する何かと考えておけば十分です。
なお車の免許を取るときに教習所で制動距離を勉強します。今後のためにも、制動距離という言葉くらいは覚えておきましょう。

ボールが落ちる運動

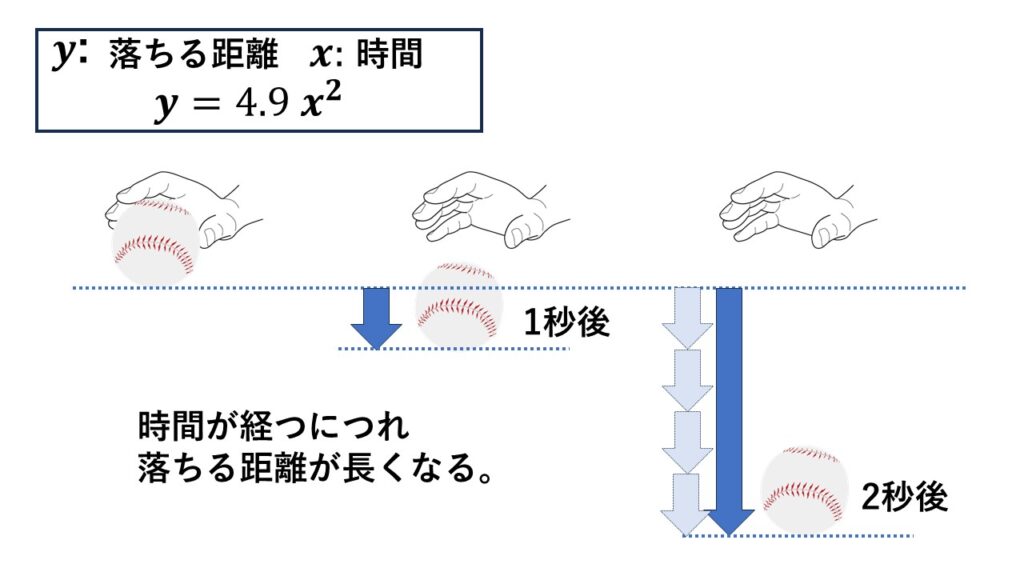
ある物体を落とすとき、落ち始めてから$x$秒間に落ちる距離を$y$mとすると、$y$は$x$の2乗に比例し$y=4.9x^2$の関係があるといいます。

これは時間が経つにつれ、落ちる距離が長くなることを表しています。

この$4.9$がどこから出てきたのかについては高校で詳しく学ぶので、中学の段階では特に気にせず軽く覚えておいてください。

直方体の体積

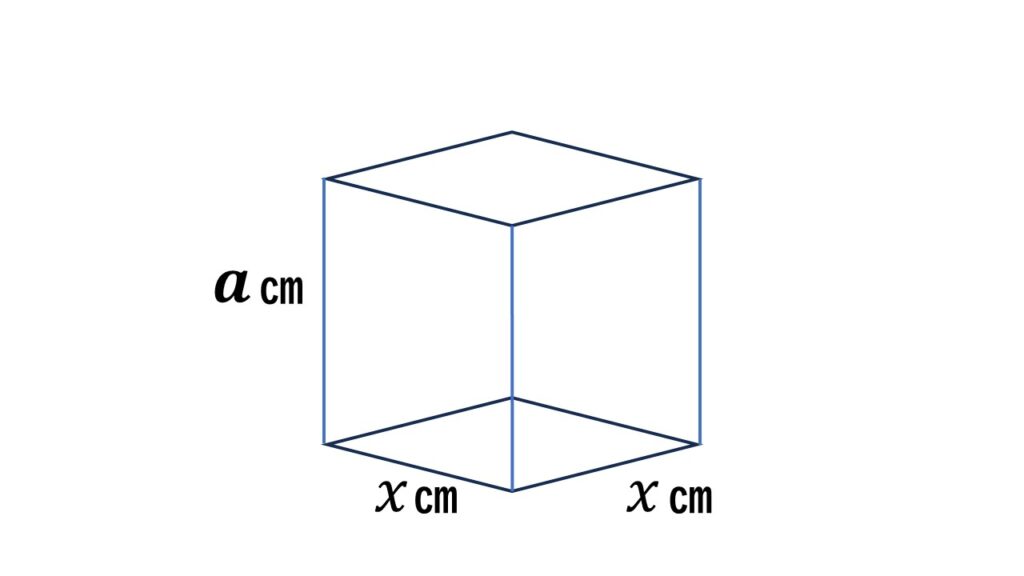
縦$x$cm、横$x$cm、高さ$a$cmの直方体の体積$y$cm$^3$は
$y=ax^2$となります。

直方体のプール（そんなのがあるかどうかわかりませんが）の体積をイメージしてください。
$y$は$x$の2乗に比例する関係式そのものですね。

これらは日常生活に関わる具体例ではありますが、今一つ実感がわかないのが正直なところだと思います。
それもそのはず。
そもそも日常生活で2乗を考えることが自体があまりありません。
そのため、個数と代金の関係のように、日常の直接的な例としては挙げにくいのです。

制動距離も落下運動も、色々調べた結果として$y=ax^2$の関係を導けたと考えてください。

それでは制動距離についての例題を解いてみましょう。

基本例題
時速$x$kmで走るときの制動距離を$y$mとすると、$y$は$x$の2乗に比例する。
よしお君が乗っている自慢の車は、時速$40$kmで走るときの制動距離が$10$mだという。
このとき次の問いに答えよ。
$(1)\:x$と$y$の関係を式に表せ。
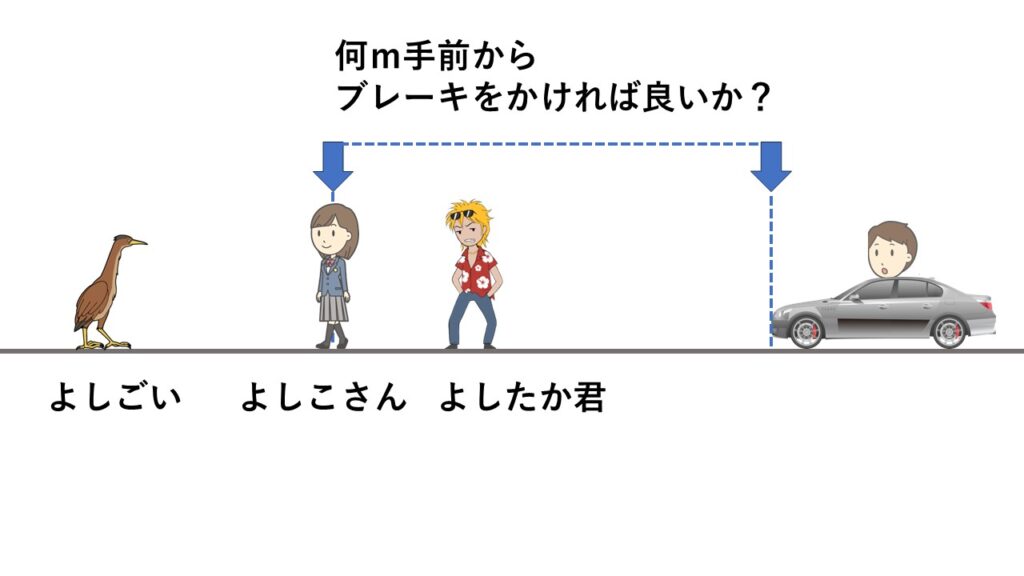
$(2)\:$よしお君は運転中によしこさんを見つけた。隣に乗せてドライブデートに誘おうと思う。時速$20$kmで走っているが、このときの制動距離を求めよ。

考え方
$(1)\:$制動距離の問題で「$x$と$y$の関係を式に表せ」とあったら$y=ax^2$とおきます。
$x$と$y$にそれぞれ代入し$a$を求める。超基本例題の解き方と同じです。
$(2)\:$$(1)$で求めた式を使って制動距離を求めます。

解答
$(1)\:$求める式を$y=ax^2$とおく
　時速$40$kmで走るときの制動距離が$10$mなので
$\quad\begin{align}10&=a\times40^2\\\\10&=1600a\\\\a&=\dfrac{10}{1600}\\\\a&=\dfrac{1}{160}\end{align}$

　よって求める式は$\quad y=\dfrac{1}{160}x^2$

$(2)\:y=\dfrac{1}{160}x^2$より時速$20$kmなので

$\begin{align}\quad y&=\dfrac{1}{160}\times20^2\\\\y&=\dfrac{400}{160}\\\\y&=2.5\end{align}$

よって制動距離は$2.5$m

$(2)$別解
時速$x$kmで走るときの制動距離を$y$mとすると、$y$は$x$の2乗に比例するので
速さが$\dfrac{1}{2}$になれば制動距離は$\dfrac{1}{4}$となる
したがって
$10\times\dfrac{1}{4}=2.5$m

解説
制動距離の問題のほとんどは、問題文中に「時速$x$kmで走るときの制動距離を$y$mとすると、$y$は$x$の2乗に比例する」との説明書きがあります。
なぜなら制動距離の関係式を覚える（暗記する）必要がないからです。
そのため制動距離の文言を見た時点で$y=ax^2$を瞬時に思い出せるようにする必要はありません。
でもまぁ、覚えておいて損はありません。

$(2)$の別解は、問題の条件である「時速$40$kmで走るときの制動距離が$10$m」を使っています。
速さが半分なら、制動距離は半分の半分、つまり$\dfrac{1}{4}$となります。

なお、よしこさんを見つけたよしお君が嬉しさのあまり、カッコつけようとしてドリフトし始めたなどといったことは考える必要はありません。そんなことまで考えたら問題のレベルが爆上がりします。

参考までに、覚える必要はありませんが一般的に時速$40$kmで走る車の制動距離はだいたい$22$mだそうです。
よしお君の車はやっぱり性能が良い自慢の車のようです。

なぜ中学の教科書では二次関数と言わないのか？

ところで、中学3年生が使う数学の教科書には二次関数という言葉は載っていないと思います。
$y=ax+b$の形をした関数を一次関数と言いました。$x$の一次式なので一次関数ということですね。ならば

今勉強している
$y=ax^2$は$x$の二次式だから二次関数と言うのではないか？

そう考えたキミは鋭い!!

確かに$y=ax^2$は二次関数です。間違いありません。
ただ$y=ax^2$は極めて特殊な二次式です。

通常二次式と言ったら、$x$1乗の項もあり数値だけの項もある$ax^2+bx+c$の形のものを指します。
で、$b$と$c$がそれぞれ$0$のときのものが、極めて特殊な$y=ax^2$のわけです。

中学で学ぶ二次関数は$y=ax^2$のみです。
$y=ax^2+bx+c$の形をした一般の二次関数は高校で学びます。
つまり$y=ax^2$は確かに二次関数ではあるけど、一般的な$y=ax^2+bx+c$を学ばないうちに二次関数と言ってしまうのはあまりよろしくない。
そのため中学3年の数学の教科書では二次関数と言わないようにしています。