中学で扱う文章題の中でも難しい部類に入るのが割合や濃度%に関する問題です。ただでさえ割合や百分率を難しく感じるのに、そこに文字が絡んで方程式の応用問題になってくると難しさがさらに増します。
ここでは割合や濃度の応用問題に対応できるよう割合の基本事項から、いや、小学校で学んだ分数の基本から徹底して復習します。
10分の3とは?
10分の3とは、「10個に分けたうちの3個ぶん」ということです。当たり前だ!! と思わないでくださいよ。割合を考える際はこのことに大きなポイントがあります。
例えばピザ1枚を10等分する時、その式は
$1\div10$で$\dfrac{1}{10}$です。
その10等分したものが3個あったとします。
その時の式は、$\dfrac{1}{10}$が3個あるということで
$\dfrac{1}{10}\times3$ つまり $\dfrac{3}{10}$になります。
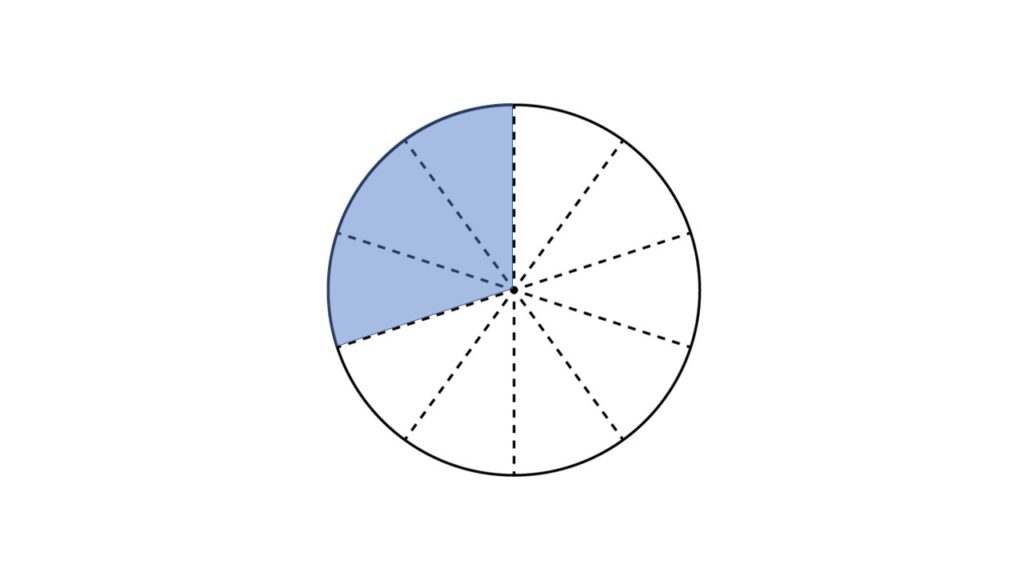
何を言いたいのかというと、
10個に分けたうちの3個ぶんを式で表したものが
$\dfrac{3}{10}$だということ。
いいですか、この当たり前なことを当たり前だと思わずに新鮮な気持ちで受け止めてくださいね。
3割とは? 30%とは?
「割」は10分の1の位の数のことです。
だから1割といったら0.1、2割は0.2、3割はもちろん0.3です。
ところで小数を分数で表すと
0.1は$\dfrac{1}{10}$、0.2は$\dfrac{2}{10}$、0.3は$\dfrac{3}{10}$です。
なので3割とは$\dfrac{3}{10}$のことです。
「1%」とは0.01のことです。
だから10%は0.1です。すると30%は0.3ということになります。
ここでしっかり確認してください。
0.3は30%で、30%は3割で、3割は0.3で、
どれも10個に分けたうちの3個ぶんということ。
つまり0.3も、10分の3も、3割も30%も、見た目は違うけど同じことを表しています。
40の10分の3はいくつ?
では超基本練習を通して割合の理解を深めましょう。
超基本練習 40の10分の3はいくつですか?
これは言い変えると、
「40を10個に分けたうちの3個ぶんはいくつですか?」
となります。このように言いかえると式はすぐに出ると思います。
まず40を10個に分けるから$40\div10$
それが3個ぶんだから$40\div10\times3$
つまり$40\times\dfrac{1}{10}\times3$ で
$40\times\dfrac{3}{10}$
ということで結果 $12$ となります。
10分の3を求めるのに、結果としてかけ算をやっていることを理解してください。
ここまでがわかれば、割合の問題の半分は理解したことになります。
ではさらに練習。
40の3割はいくつ?
3割は0.3。0.3は10分の3です。結局10個に分けたうちの3個ぶんを求めるのと同じです。
するともうわかりますよね。
答えは12です。
とどめにもう1問。
40の30%はいくつ?
30%は0.3ですよね。なのでこれも答えは12です。
割引の問題にチャレンジ
これらのことをふまえ割引の問題をやってみます。
ここは超基本を身につけることが最優先なので、超基本に沿ったかっこ悪い解き方でいきます。
学校や進学塾ではおそらくこんな解き方は教えません。
練習問題 100円の3割引きはいくらですか?
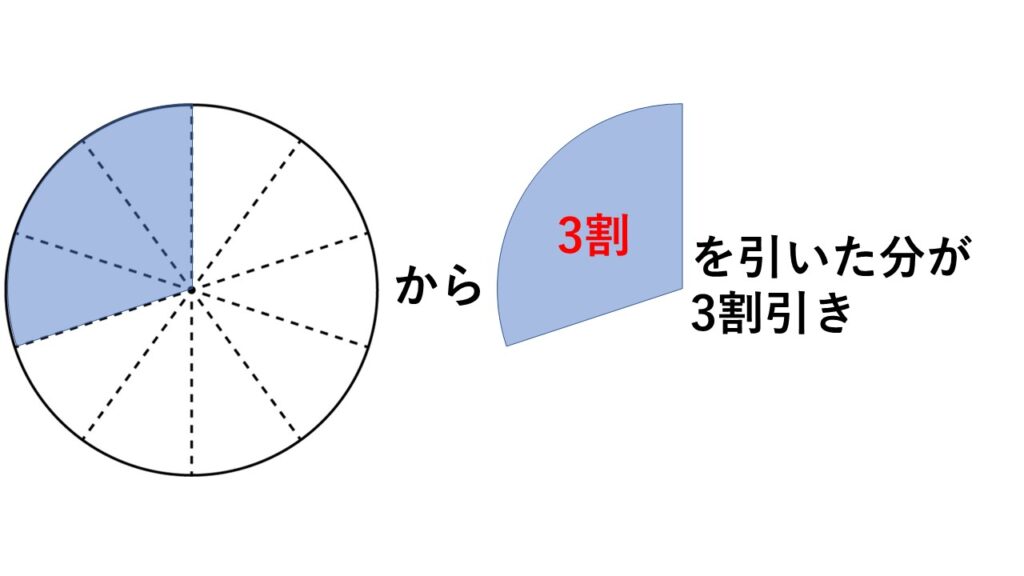
考え方 3割引きだから当然「3割を引く」。
「100円から100円の3割を引く」ということ。
以下の手順で解きます。
①100円の3割を求める
②100円から①で求めた値を引く

解答 100円の3割は
$100\times\dfrac{3}{10}$
$=10\times3=30$ より30円。
よって100円の3割引きは
$100-30=70$ で 70円となる。
学校や進学塾ではこの様な解き方ではなく、謎の計算「$1-0.3$」が途中で出てくるはずです。
本当に割合を苦手としていると、この「$1-0.3$」が本当にわからないんですよね。1って何よって感じで。(自分がそうでした・・・)
ちなみに学校や進学塾で教わる普通の解き方は
$100\times(1-0.3)$
$=100\times0.7=70$
だと思います。
謎の$1-0.3$が出てきて、さらになぜかかけ算出てくる謎が謎を呼ぶ解き方。
突然こんな解き方をされたら誰だって?????となります。
このページでは$1-0.3$が何なのかはあえて放置しておきます。
割引について苦手意識を持っている人はまず、練習問題の解き方をしっかり理解してください。
これをふまえて次の練習に移ります。
練習問題2 $a$円の3割引きはいくらですか?
考え方 文字を含んでもやり方は同じ。
「$a$円から$a$円の3割を引く」ということ。
①$a$円の3割を求める
②$a$円から①で求めた値を引く
この手順でいきます。
解答 $a$円の3割は
$a\times\dfrac{3}{10}$ より $\dfrac{3}{10}$$a$ 円。
よって$a$円の3割引きは
$a-\dfrac{3}{10}$$a$
$=\dfrac{10}{10}$$a$$-\dfrac{3}{10}$$a$
$=\dfrac{7}{10}$$a$ 円。
数学に慣れていないと分数に文字がついた形を見ただけで正解かどうか不安になりますが、これも立派な解答です。
ではもう1問練習問題。
練習問題3 $a$円の30%引きはいくらですか?
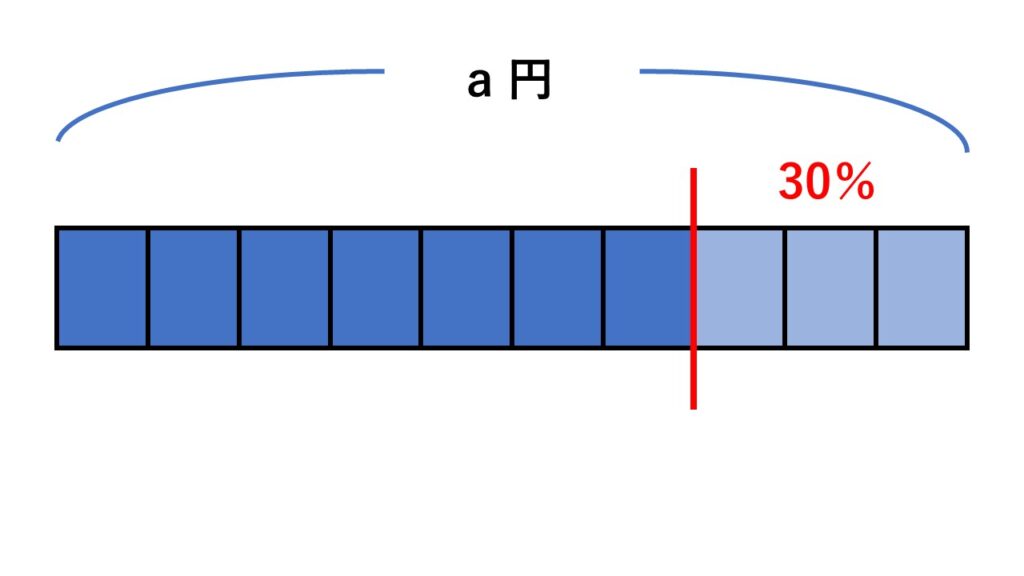
考え方 「$a$円から$a$円の30%を引く」ということ。
やり方は同じ。
$a$円がいくらなのか具体的なことは考えない。
解答 $a$円の30%は
$a\times\dfrac{3}{10}$ より $\dfrac{3}{10}$$a$ 円。
よって$a$円の30%引きは
$a-\dfrac{3}{10}$$a$
$=\dfrac{10}{10}$$a$$-\dfrac{3}{10}$$a$
$=\dfrac{7}{10}$$a$ 円。
ここまでのまとめ
ここまで理解できれば、割合についての基本は学習できたことになります。
割合の問題は1つ1つをしっかりかみ砕いて考えていくと、実はそれほど難しいことをやっているわけでもないとわかると思います。
割合の問題で苦手意識を持ってしまうのは、ここまでの内容を理解しないうちに難易度の高い問題をやってしまったから。
なので割合の問題で行き詰ってしまったときは、このページで紹介した問題を振り返ってください。
今さら聞けないちょっと恥ずかしいことも解決できると思います。
