通過算とは
通過算とは、
列車のような長い物が、
ある地点、あるいはトンネルや鉄橋などある程度の距離がある物を、
完全に通り過ぎる時の速さや時間などを求める問題
のことをいいます。
通過算は主に4つの問題パターンがあります。
通過算の4つの問題パターン
- 人や踏切など、ある地点を通過するパターン
- トンネル、鉄橋、駅など、ある程度の長さがある物を通過するパターン
- 列車同士がすれ違うパターン
- 一方の列車がもう一方の列車を追い越すパターン
中でも①の人や踏切など、ある地点を通過するパターンの問題は、通過算の問題の全ての基本になる考え方が詰まっています。
通過算を難しく感じてしまっている人は、まず①のパターンの考え方をしっかり覚えてしまいましょう。
通過算の解き方 人や踏切など、ある地点を通過するパターン
では実際に通過算の例題を使って解き方を見ていきます。
通過算を考える時は簡単なイラストを描いていくと、列車の動きを考えやすくなります。
ということで次の例題を考えてください。
ちなみに地点といわれたら、点として考えます。長さは考えません。
【例題】
長さ120mの列車が秒速20mで走っている。
この列車が撮り鉄君の前を通過するのにかかる時間は何秒か?
イラストを描いて、列車の動きと撮り鉄君の関係をしばらく考えてくださいね。

通過算を難しく感じてしまう原因の1つに、
通過するとはどういうことか? というのがあります。
「通過」を考える時に重要なのが、列車の先頭部分と列車の最後尾。
列車の先頭や最後尾と撮り鉄君の位置関係に注目して考えます。
解き方は実際に動いているものを見た方が理解しやすいと思うので、次の動画で理解していきましょう。
ポイントは
列車の長さと、撮り鉄君の前を通過する時に列車が走った距離が同じだということ。
このことに気づければ、後は道のり、速さ、時間の関係式に当てはめれば求められます。
この例題は通過算の全ての問題の基本となるので、通過算の問題を解いていて考え方に行き詰った時はこの例題を思い出してください。
「列車の長さ」についてはつい忘れがちなので、しっかり覚えておきましょう。
ということで、列車がある地点を通過するパターンの問題を理解できたら、次のパターンの問題を練習していきます。
鉄橋やトンネル、駅など、ある程度の長さがある物を通過するパターン
次に列車が鉄橋やトンネル、駅を通過するパターンの問題の解き方を考えます。
それでは早速例題から。
【例題】
長さ140mの列車が420mの鉄橋を渡りはじめてから渡り終わるまでに40秒かかった。
この列車の速さは時速何㎞か?
このタイプの問題も列車の位置関係に注目します。
「渡り始め」とはどういった状態のことか?
「渡り終わる」とはどういった状態なのか?
やはりこのタイプの問題も「列車の長さ」がポイントになります。
これらの状態をしっかり見極めないといけません。
イラストを描きながらしばらく考えてみましょう。
ある程度考えてから次の動画へ。
鉄橋の問題では、
「渡り始め」を列車が先頭が鉄橋に入った瞬間、
「渡り終わる」を列車の最後尾が鉄橋を抜け切る瞬間、
として考えていきます。
このことに気づけないとなかなか解答を出せません。
そして「渡り終えた時の列車が走った距離」をしっかり導けるかどうかが、この問題を正解できるかの分かれ目。
鉄橋の長さと、列車自身の長さを足したのもが、渡り終えた時の列車が走った距離となります。
動画を参考に列車の位置関係と走った距離について理解をしてください。
パターンごとに解き方を暗記するのではなく、理解してください。
鉄橋やトンネルを通過するパターンの問題を理解できたら、次のパターンにチャレンジしてみましょう。
一方の列車がもう一方の列車を追い越すパターン
ここからは通過算の中でも少しレベルの上がった内容になります。
とは言っても、最初の撮り鉄君の問題と鉄橋の問題の解き方を理解していれば実はそれほど難しい問題でもありません。
次の例題の解き方が腑に落ちない場合は、もう一度撮り鉄君の問題と鉄橋の問題を振り返ってみてください。
ということで追い越すパターンの例題。
【例題】
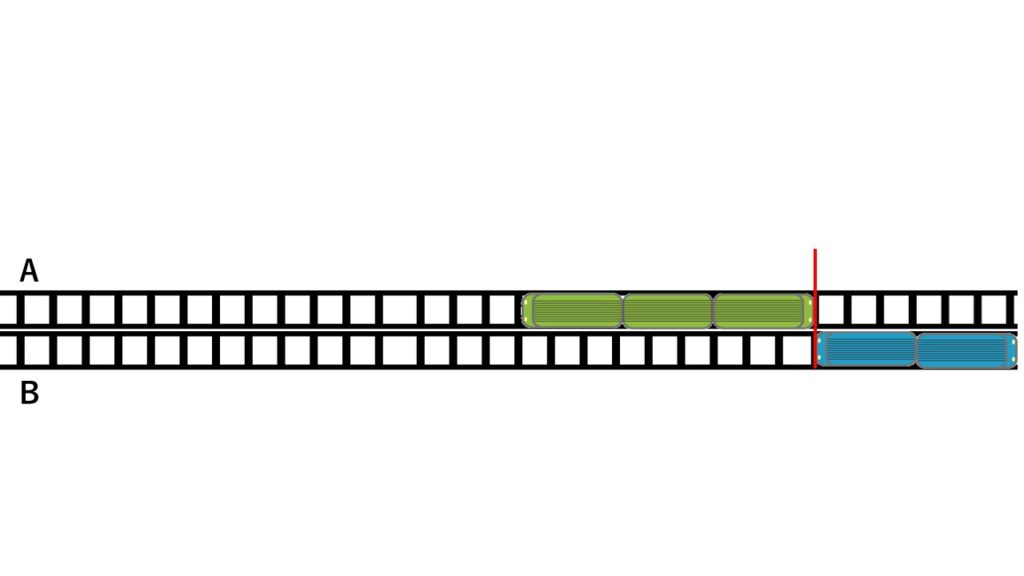
長さ100m、時速36㎞の列車Aと、長さ80m、時速45kmの列車Bが同じ方向に走っている。
列車Bが列車Aに追いついてから追い越すまでにかかる時間は何秒か?
まずは自分でしっかり考えてくださいね。
追い越すパターンの問題では、
「追い越す」とはどういうことなのか
を考えることが重要です。
もっとも追い越すを言葉で言うには簡単ですが、
数学の計算で考える際は、追い越す状態を考えないと計算式が作れません。
以下のイラストを参考に、
追いついてから追い越すまでにかかる時間を考えてください。
もちろん時間を求めるわけだから、
道のり、速さ、時間の関係式を使います。
ここもポイントは「列車の長さ」です。
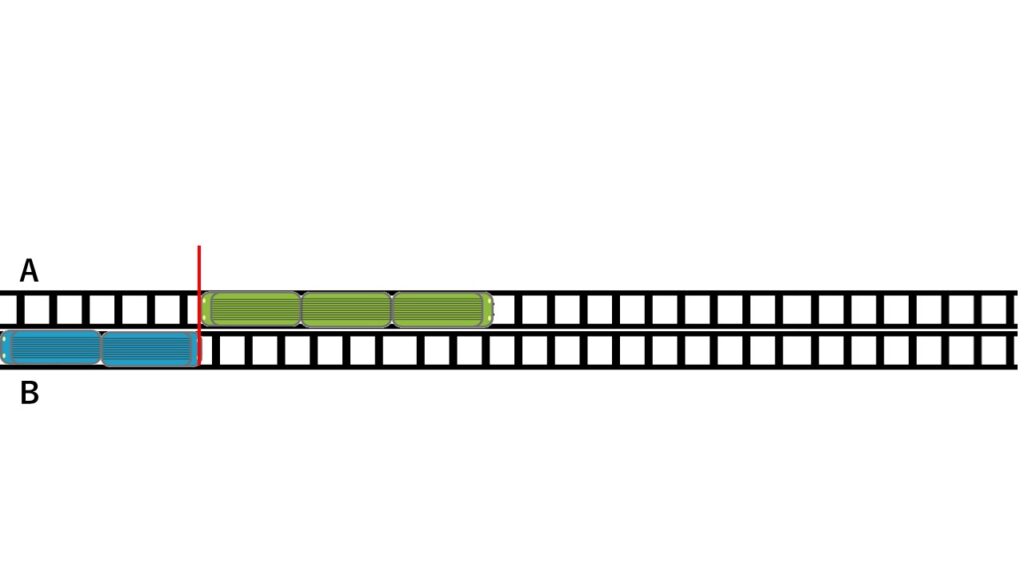
しっかり自分で考えてから動画を観てくださいよ。
追い越すパターンの問題のポイントは、
追い越される列車は止まっているもの、つまり速度0とみなして考えます。
そして追い越す側の列車の速さは、追い越される列車の速さの分だけ遅く走っているとみなします。
このように、問題に提示された速さのままで考えるのではなく、
視点を切り替えて速さを考える所に、追い越すパターンの問題の難しさあります。
このことに気づけないと先に進めなくなってしまいます。
逆にこのことに気づけると、次に紹介する電車同士がすれ違うパターンの問題も意外と簡単に解ける様になってきます。
ということで、追い越すパターンの解き方が理解できたらすれ違うパターンに進みましょう。
列車どうしがすれ違うパターン
すれ違うパターンの問題では、計算式を立てるまでの考え方にちょっとした視点の切り替えが必要になります。
では実際に例題を使って考えてみましょう。
【例題】
長さ100m、時速36㎞の列車Aは東へ進み、長さ 80 m、時速45㎞の列車Bは西へ進んでいる。
列車Aと列車Bが出会ってからすれ違い終わるまでに かかる時間は何秒か?
すれ違うパターンの問題を難しく感じてしまうのは、速さの手がかりが2つ与えられているから。
そのため速さをどう扱えば良いのかが見えなくなってしまいます。
速さをどう扱うかが解法のポイント。
このことをよく考えてから動画を観てください。
道のり、速さ、時間の関係式を使うために、2つの列車の動きと長さの関係に気づけないとなかなか解法が見えてきません。
2つの列車がすれ違うパターンの問題では
(2つの列車の長さの和)÷(2つの列車の速さの和)
を計算すればすれ違いにかかる時間を一瞬で求められます。
関係さえわかってしまえば、瞬間的に計算式を立てられることもわかったと思います。
ただ動画内でも書きましたが、解き方を暗記するのではなく、式を立てるまでの列車の動きの過程を理解してください。
通過算の問題を公式として解こうとするのはあまりお勧めしません。
