多角形の内角の和の求め方

多角形の内角の和は
$180\times(n-2)$　を計算すると求められます。

$n$とは角の数のこと。
例えば三角形の内角の和を計算で求める場合は$n=3$を代入し
$180\times(3-2)=180$として求められます。
ではなぜこの式で内角の和を求められるのか？
このページでは内角の基本からじっくり説明していきます。

内角とは

内角とは、多角形で隣り合う2辺がつくる図形の内部にある角のことをいいます。
ここでは単純に、図形の内部にある角と覚えておきましょう。

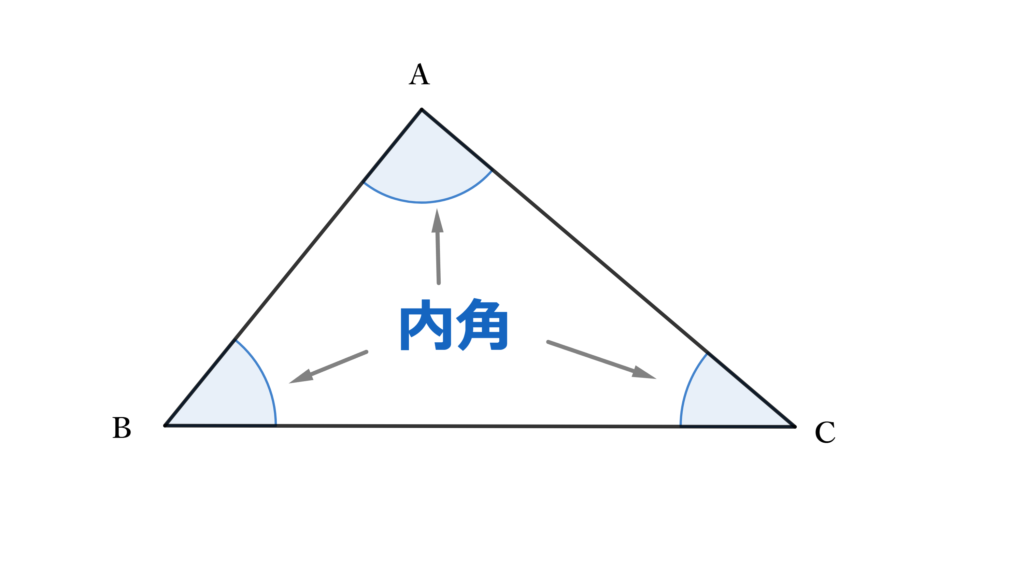
三角形の内角の和は$180°$と小学校で習っていますね。
でも小学校のときは$180\times(n-2)$の式を教わっていないはずです。
なのに三角形の内角の和は$180°$と教わっている。
ならばどこから$180$という数値が出てきたのか？

三角形の内角の和が180°となるわけ

三角形の内角の和は$180°$となることを説明するには角度の定義（取り決め事という意味）から説明が必要になります。
ただそれを説明するとこのページの本質からそれるので、ここでは単純に直線の角度は$180°$になると思ってください。

多角形の内角の和を求める計算式

ならばどうして多角形の内角の和は$180\times(n-2)$として求められるのか？
ここで三角形の内角の和が$180°$であることを使います。

四角形の内角の和を考えてみます。
四角形の内角の和は$360°$ということは次のように説明できます。

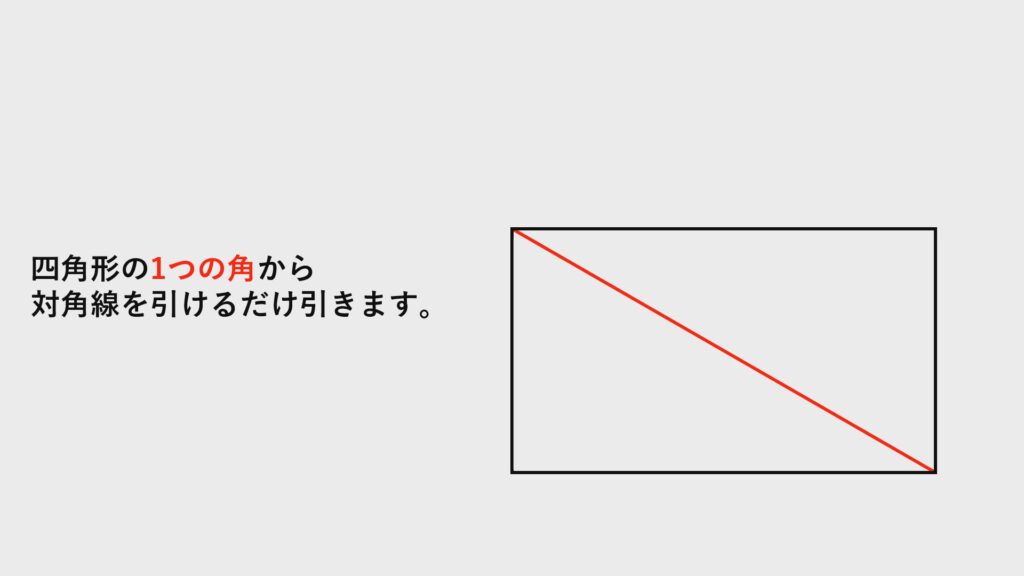
四角形の$1$つの角から対角線を引きます。
$2$つ以上の角からは引きません。

すると三角形が$2$つできます。

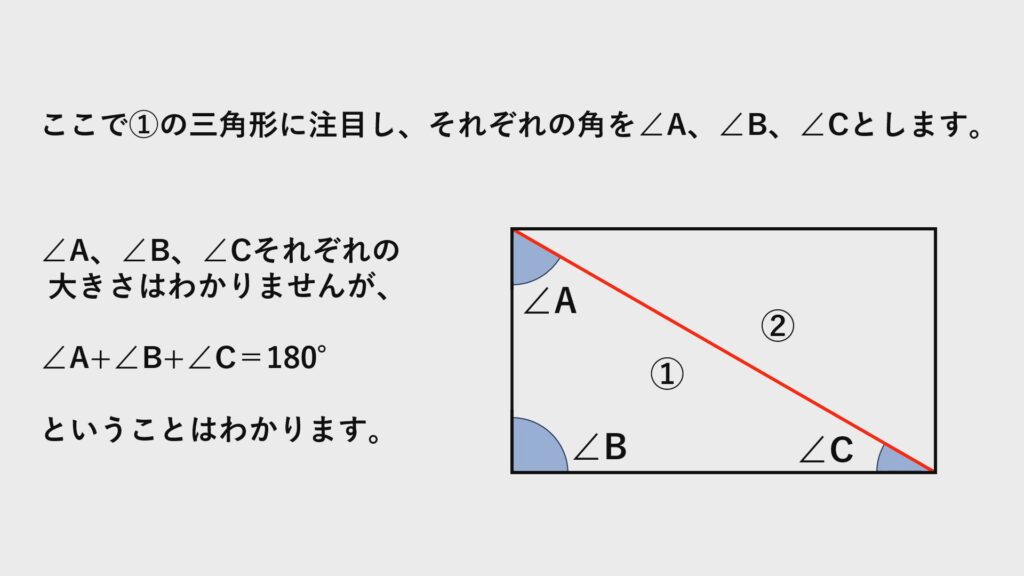
うち$1$つの三角形に注目。
それぞれの角を$∠A、∠B、∠C$とします。
三角形の内角の和なので
$∠A+∠B+∠C=180°$
となります。

もう$1$つの三角形も同様に、それぞれの角を$∠D、∠E、∠F$とすると
$∠D+∠E+∠F=180°$
となります。

結果として三角形の内角の和を$2$つ合わせたことになるので、$360°$と求まるわけです。
$180\times2$ともいえますね。

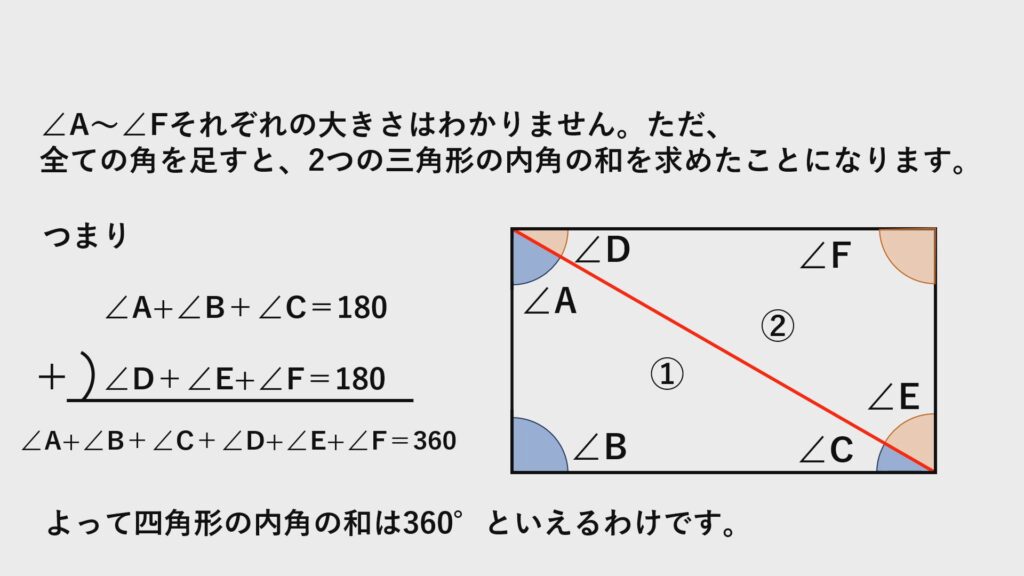
このように対角線を引いて三角形を作りその三角形の内角の和を考えていくと、多角形の内角の和を導くことができます。
五角形、六角形についても同様に見ていましょう。

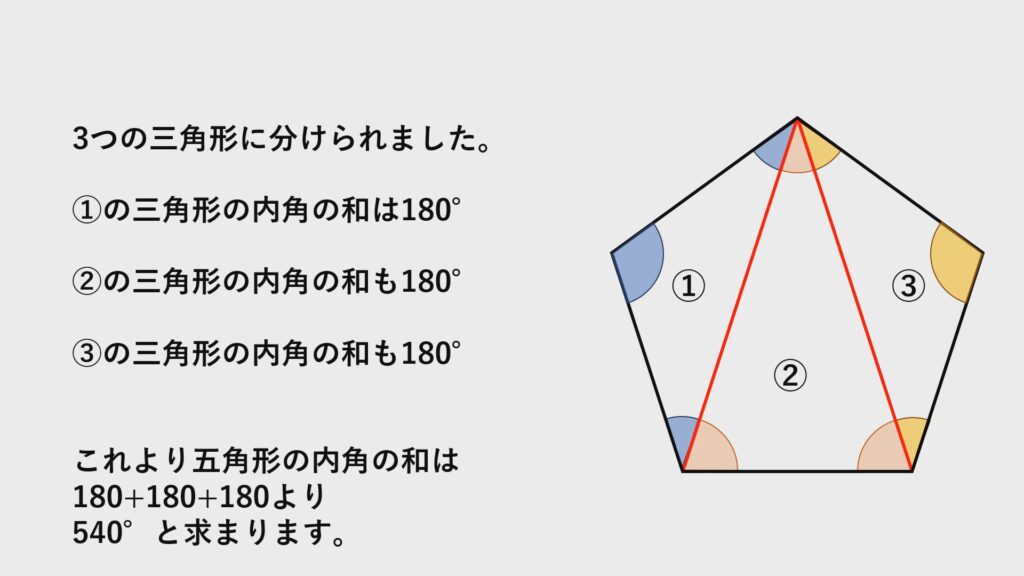
五角形の内角の和

$1$つの角から対角線を引けるだけ引きます。
すると五角形には$3$つの三角形ができます。

それぞれの三角形の内角の和を足すと$540°$と求まります。
$180\times3$と考えても同じですね。

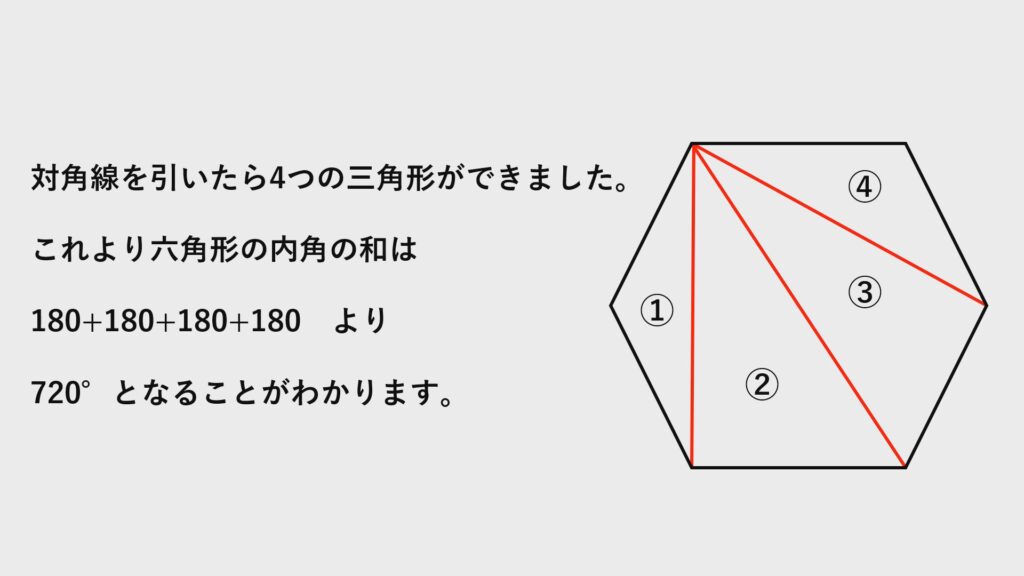
六角形の内角の和

六角形では$3$本の対角線を引けます。
すると$4$つの三角形ができます。

それぞれの三角形の内角の和を足すと$720°$と求まります。
$180\times4$と考えても同じですね。

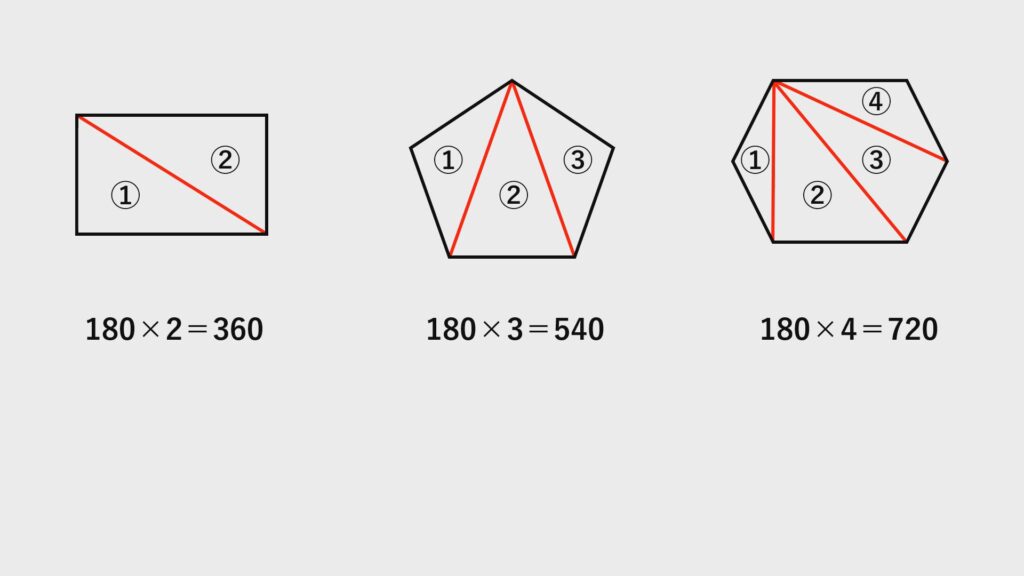
多角形の内角の和の規則性

ここまでを振り返ると、どうやら多角形の内角の和には何か規則性があるようです。

七角形、八角形も対角線を引いて規則を見つけてみましょう。

対角線を引くと、
七角形には三角形が$5$つ
八角形には三角形が$6$つ
できます。
ここで少し考えて規則性を見つけてみてください。

ここで気づいてほしい規則とは

対角線を引いてできる三角形の数が、多角形の角の数より$2$少ないこと

多角形の内角の和を求めるとき、三角形の内角の和を足していきましたが、
結果として
$180\times$三角形の数
を計算しているのと同じことでした。
そして三角形の数は角の数より$2$少ない。つまり

$n$角形に対角線を引くと$(n-2$)個の三角形ができる

とわかります。
そのため$n$角形の内角の和を求めるときは

$180\times(n-2)$　を計算すると求められるわけです。