相似な図形の体積比は相似比の3乗に等しくなる
相似比の考え方は体積にも応用できます。
それが「相似な図形の体積比は相似比の3乗に等しくなる」こと。
まずは上記の性質があるということを覚えましょう。
なお相似な図形の体積比と相似比の関係は、面積比の内容とも関わってきます。
相似比と面積比の関係も合わせて確認しておきましょう。
なぜ相似な図形の体積比は相似比の3乗に等しいのか
立体の体積の求め方はざっくり言ってしまえば
底面積$\times$高さ
です。
そこからさらに○○錐ならば$\times\dfrac{1}{3}$しますが、これは一定の数をかけることになるので、計算上は面積の一部とみなすことができます。
つまり〇〇錐の体積についても、$\times\dfrac{1}{3}$を先に底面積に施してしまえば、計算上は底面積$\times$高さと同等となります。
よって「〇〇錐の比」を考える際は、$\times\dfrac{1}{3}$を気にする必要はありません。
多角柱や多角錐の相似比と体積比
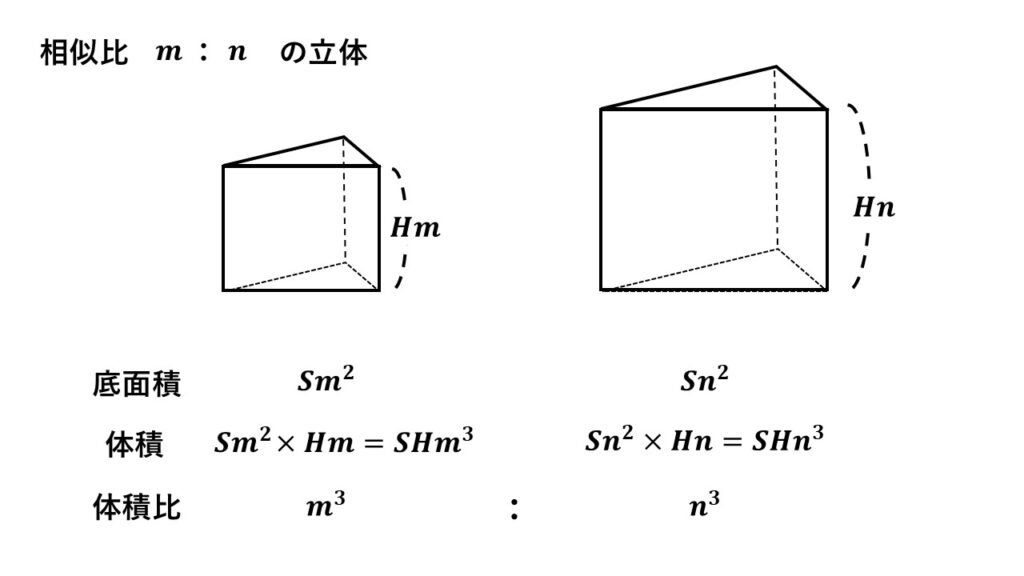
図は相似比$\:m:n\:$の三角柱です。
相似な図形の面積比は相似比の2乗なので、底面積はそれぞれ
$\:Sm^2\:$と$\:Sn^2\:$
と表せます。
また高さはそれぞれ$\:Hm,Hn\:$と表せるので体積は
$SHm^3,SHn^3$となります。
よって体積比は
$m^3:n^3\:$と求まります。
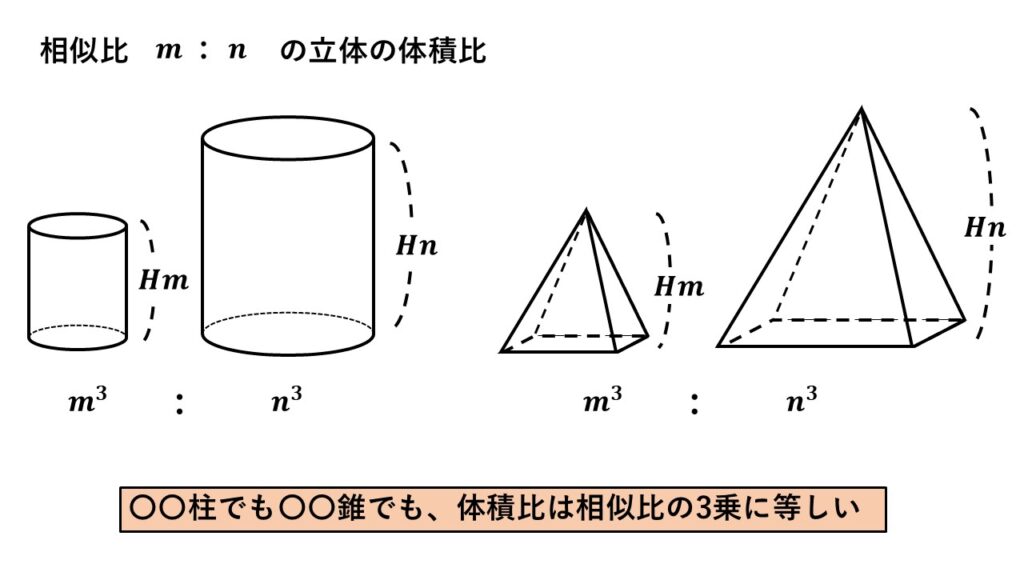
もちろん三角柱だけでなく多角柱や円柱、多角錐や円錐などに対してもいえます。
三角柱の計算をもとに、円柱や三角錐について体積を文字式で表してみてください。
結果的に相似比$\:m:n\:$の立体の体積比は相似比の3乗に等しいことがわかります。
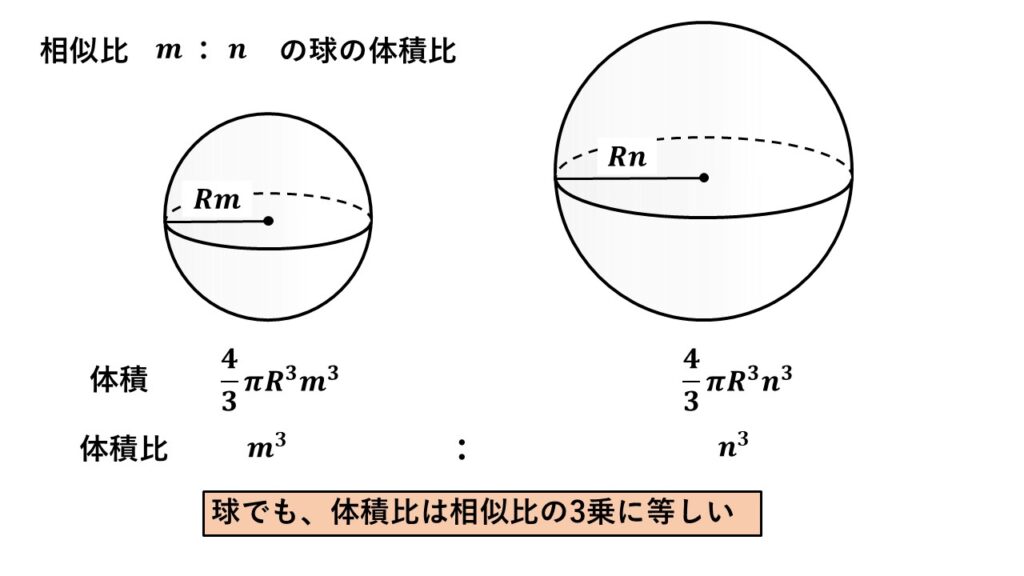
球の相似比と体積比
球についても体積比は相似比の3乗に等しくなります。
球の体積は$\dfrac{4}{3}\pi\times($半径$)^3$で計算できました。
忘れていた人はここで思い出しておきましょう。
ここまで最優先で覚えることは
相似な図形の体積比は相似比の3乗に等しくなる です。
それが成り立つ理由については、次の基本例題をしっかり解けるようになってからで十分です。
基本例題は
・基本中の基本を確認するもの
・誰でも1度は間違える円錐を使った問題
・買い物するときにどちらを買ったほうが得かを考える問題
の3問あります。
特に3問目は、相似の関係を知らないうちに日常でも使っていたと思える内容です。
それでは基本例題を使って、相似比と体積比の関係の理解を深めましょう。
相似比と体積比の基本問題
基本例題1
2つの相似な立方体があり相似比は$\:2:3\:$である。
$(1)\:$このときの体積比を求めよ。
$(2)\:$小さい立方体の体積が$64cm^3$のとき、大きいほうの立方体の体積を求めよ。
考え方
$(1)$がわからない人は冒頭のPOINTを216回繰り返し読んでください。
$(2)$体積比がわかったら比例式で計算しましょう。
解答
$(1)\:8:27$
$(2)\:$大きいほうの立方体の体積を$x$とすると
$\begin{align}\quad8:27&=64:x\\8x&=1728\\x&=216\end{align}$
解説
この基本例題1はテストで出題されたら必ず正解できなければいけません。
これを間違えたら体積比の問題は1問も解けなくなってしまいます。
基本例題2
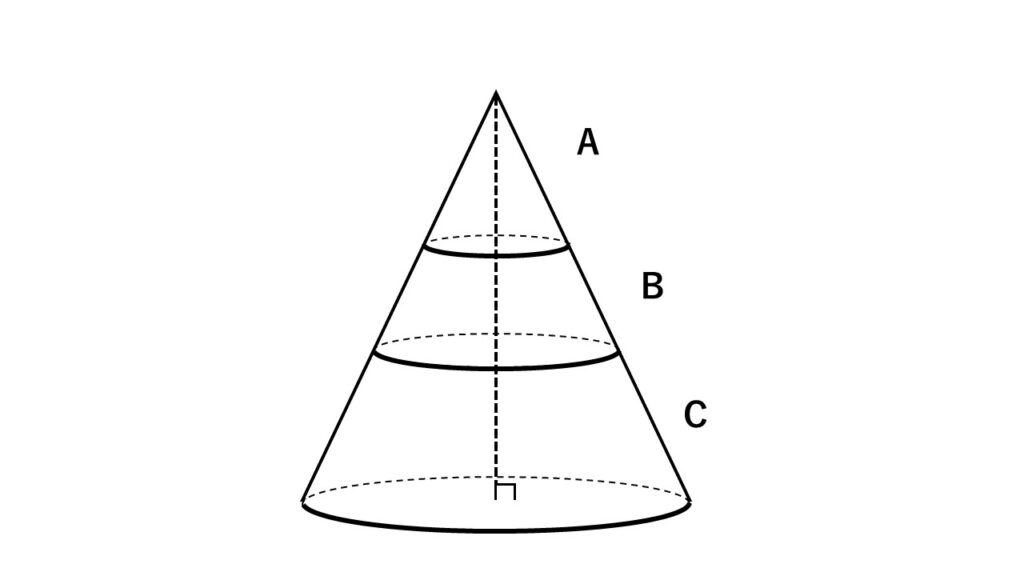
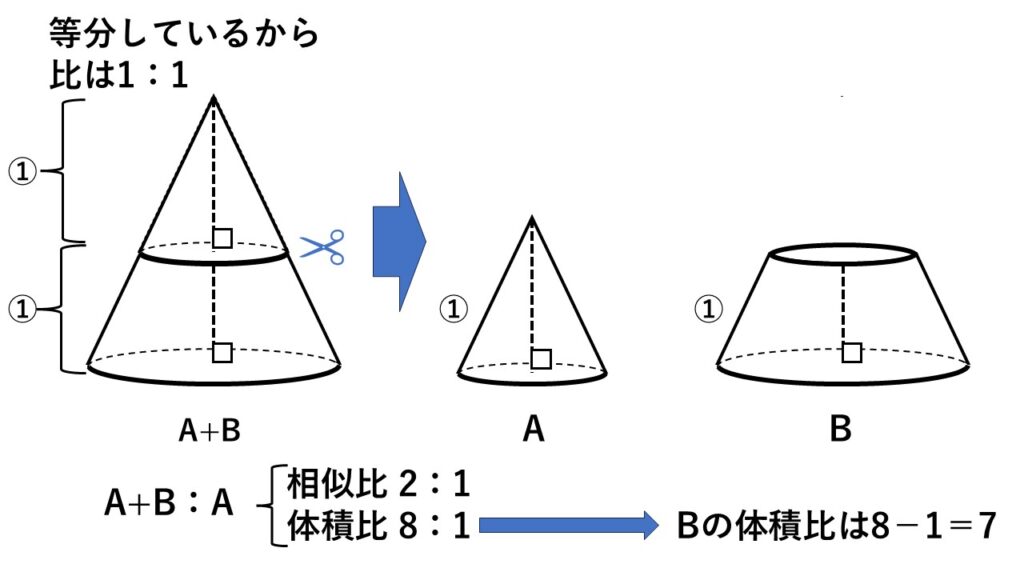
図は、円錐を底面と並行な平面で高さを3等分したものである。
このときできる立体を上から順に$A,B,C$とする。
$(1)\:A$と$B$の体積比を求めよ。
$(2)\:A$と$C$の体積比を求めよ。
$(3)\:A$の体積が$10cm^3$のとき、$C$の体積を求めよ。
考え方
等分する、つまり切り分けるため$A$は円錐ですが、$B,C$は円錐ではないことに注意。
そのため相似比を単純に3乗しただけでは誤答になります。
$(3)\:$体積比に注意して比例式で求めましょう。
解答
$(1)\:$$A$と$B$を合わせた円錐と円錐$A$は相似でその相似比は$2:1$
これより体積比は$8:1$
$\quad B$の体積は$A$と$B$を合わせた円錐から円錐$A$を引いたものなので
$\quad8-1=7$
したがって$A$と$B$の体積比は
$\quad1:7$
$(2)\:$3等分する前の元々の円錐と円錐$A$の相似比は$3:1$
よって体積比は$27:1$
$\quad C$の部分は元々の円錐から$A+B$を引いたものなので
その体積比は$27-8=19$
したがって$A$と$C$の体積比は
$\quad1:19$
$(3)\:C$の体積を$x$とすると
$\begin{align}\quad1:19&=10:x\\x&=190\end{align}$
よって$\:190\:cm^3$
解説
本問は$A,B,C$とそれぞれ切り分けた出題のため、単純に相似比を3乗しただけでは操作が足りません。
そしてここが勘違いしやすいところ。
テストで時間に追われていると、等分したとわかっているのに、切ったそれぞれが新たな円錐として出てくると、ついうっかり誤った考えを持ってしまいます。
そのついうっかりを突いてくるのが定期テストや入試問題。狙われやすいです。
偉そうに書いてますが、私は中学時代にトラウマ級の散々な目に遭いました。
次に相似をちょっと応用して、どっちがお得かを考えてみましょう。
基本例題3
ある店で売ってるカップに入ったストロベリーアイスのサイズと値段の関係は、次の表のようになっている。
カップは相似の関係にあり、どちらも同じストロベリー味のアイスがカップいっぱいに入っているものとする。
ＭサイズとＬサイズではどちらを買った方が、より良い買い物をし満足感が得られると考えられるか。
その理由を相似の観点から説明せよ。
考え方
これと似たような状況が日常でもあると思います。
日常でやっていることを相似の関係から数学的に解答してみましょう。
解答
カップの直径からＭサイズとＬサイズの相似比は$4:5$
これより体積比は$64:125$となる
値段は$530\div350$よりＬサイズがＭサイズのおよそ$1.5$倍
一方、体積比は$125\div64$よりおよそ$2$倍となっている
したがって、およそ$1.5$倍の金額を払えばおよそ$2$倍の量を食べられる
よってＬサイズを買ったほうがより満足感を得られると考えられる
解説
値段と量の関係でどれだけ得したかを考えることは、普段からやっていると思います。
本問はまさにそれを数学的に考えたもの。
日常では感覚的にやって何となく得した感じだと思っているかもしれませんが、数学的に考えるとどれだけ得なのかがより正確に分かってきます。
相似はこんな形でも日常生活に応用が利いてきます。
定期テストでは本問のように、相似比の関係から理由を説明させる問題も出題される可能性があります。
まぁ説明問題なので、解法がわからなくても相似比について何かしら記載しておけば、部分点くらいは取れると思います。
なお数学の問題なので、
「僕はストロベリーよりバニラが好きだから満足しない」
とか
「私は銀座で1500円するイタリアンジェラートにラム酒で香りづけしたものをいつも買ってもらってるから、問題の意味が解りません」
など、たとえ事実であっても感情で答えるのは止めておきましょう。
