図形を考える際は必ず角について考えますが、簡単に「角」といっても、角どうしの位置関係によって呼び方があります。
ここでは角の関係について解説し、初歩的な問題を解けるようにします。
対頂角
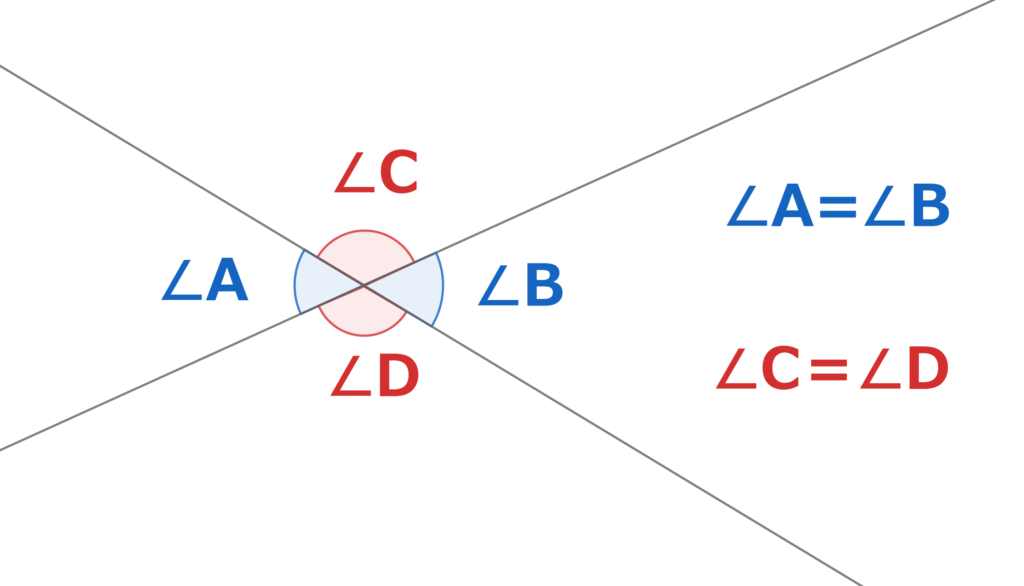
2つの直線の間にできる向かい合った角のことを対頂角といいます。
対頂角の大きさは等しくなります。
図では、
$∠A$と$∠B$が対頂角
$∠C$と$∠D$が対頂角
の関係にあります。
もし$∠A=30°$ならば$∠B=30°$となります。
ところで直線は角度で表すと$180°$ですよね。ということは
$∠A=30°$だとしたら
$∠C=180-30$より$∠C=150°$
と求めることができます。
そして$∠D$は$∠C$の対頂角だから$∠D=150°$とわかります。
同位角
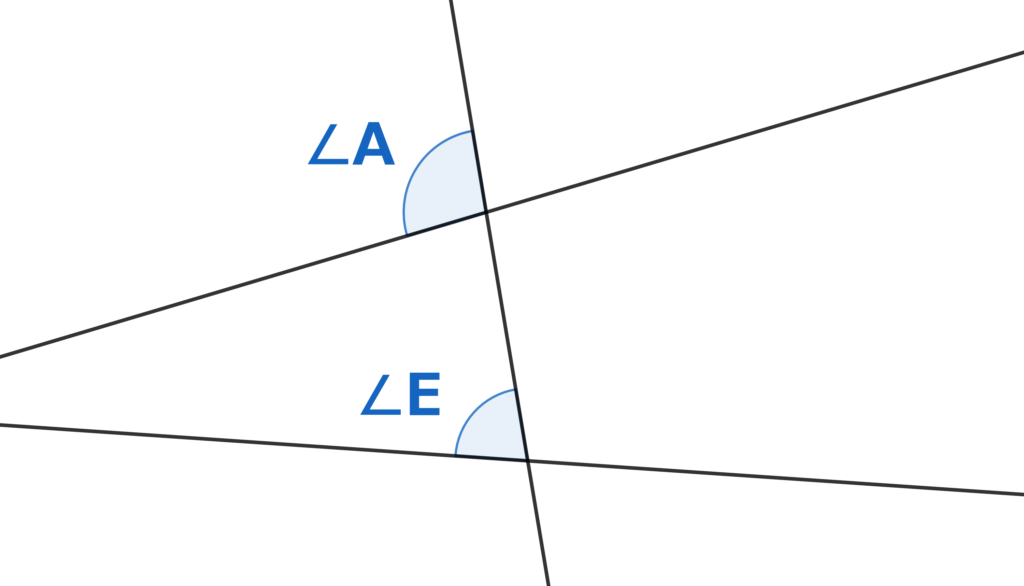
図のように2つの直線があり、その2つの直線に交わるようにもう1つ直線を引きます。
このときできる角で、
$∠A$と$∠E$のような関係を同位角といいます。
この同位角。言葉で説明するのが難しいので図で感覚的にわかってほしいのですが、それでは解説にならないので次のように覚えてください。(学校や塾ではこんな説明の仕方はしません、絶対に。)
横方向に2つ直線を引いて、それらに交わるように1つ直線を縦方向に引きます。
このときできる左上側の2つの角の関係を同位角と考えてください。
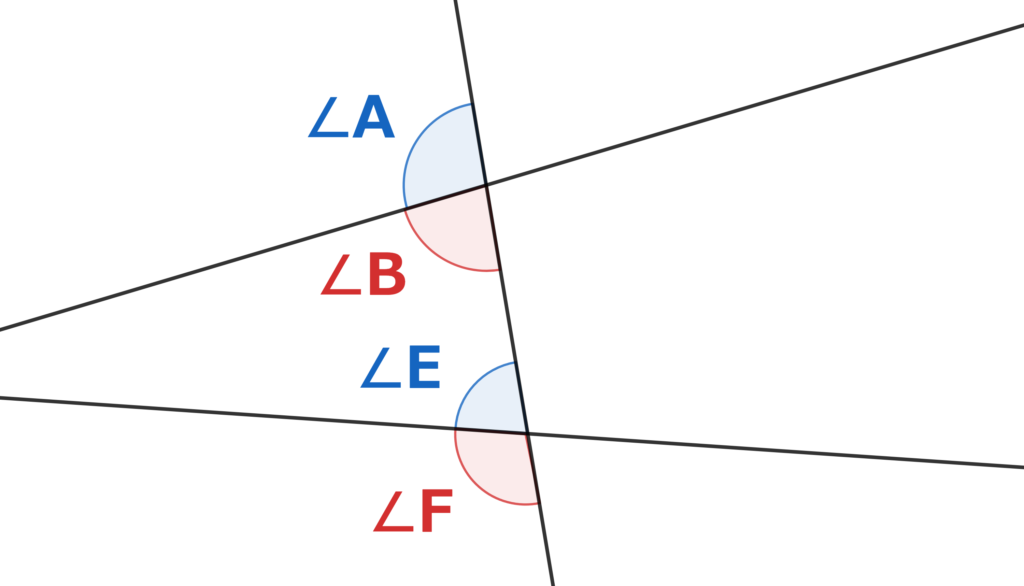
すると左上側の関係だけが同位角なのかというとそうではありません。
左下側の2つの角も同位角の関係にあります。
$∠B$と$∠F$の関係も同位角
さて、こう書くと左側の関係だけが同位角なのかというとそうでもありません。
右側についても同様なことがいえます。
右下側の2つの角
$∠C$と$∠G$の関係も同位角
右上側の2つの角
$∠D$と$∠H$の関係も同位角
の関係があります。
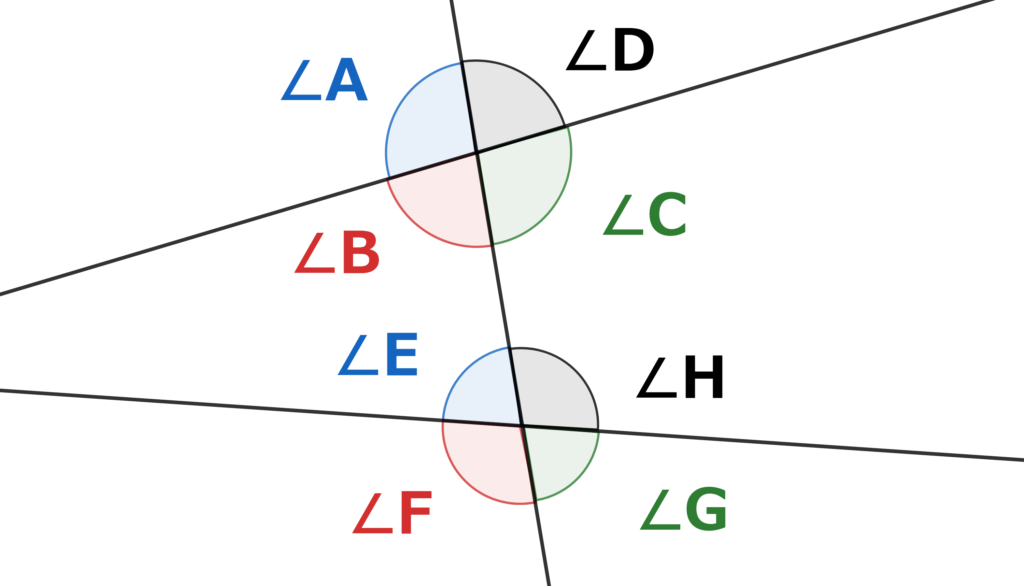
ここまで大丈夫ですか?
新しく学んでいる言葉は「対頂角」と「同位角」だけですからね。
ちなみに$∠A$と$∠C$は対頂角です。向かい合った角になってますよね。
ついでに$∠F$と$∠H$も対頂角です。
他にも対頂角の関係がありますよね。
錯角
錯角と書いて「さっかく」と読みます。
言葉で説明するのが非常に難しいですが、
2つの横線の間にあり、縦線を境に反対側にある角の関係を錯角といいます。
図で$∠B$と$∠H$の関係が錯角です。
$∠C$と$∠E$の関係も錯角です。

とにかく錯角は言葉で理解するより、図を見て覚えてください。
ところでここまで2つの横線と曖昧な書き方をしましたが、2つの横線が平行のときに、角に関する重要な性質ができてきます。
次に少し発展させて平行線と角の関係を見ていきます。
平行線と角
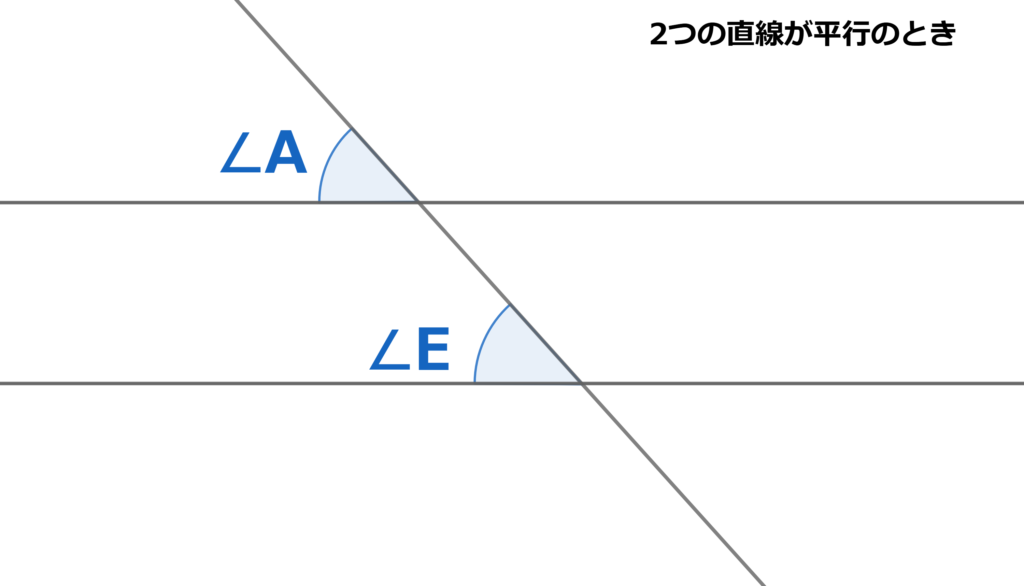
図より$∠A$と$∠E$は同位角の関係です。
このとき
2つの横線が平行ならば同位角は等しくなります。
$∠A=∠E$
このことをしっかり理解してください。
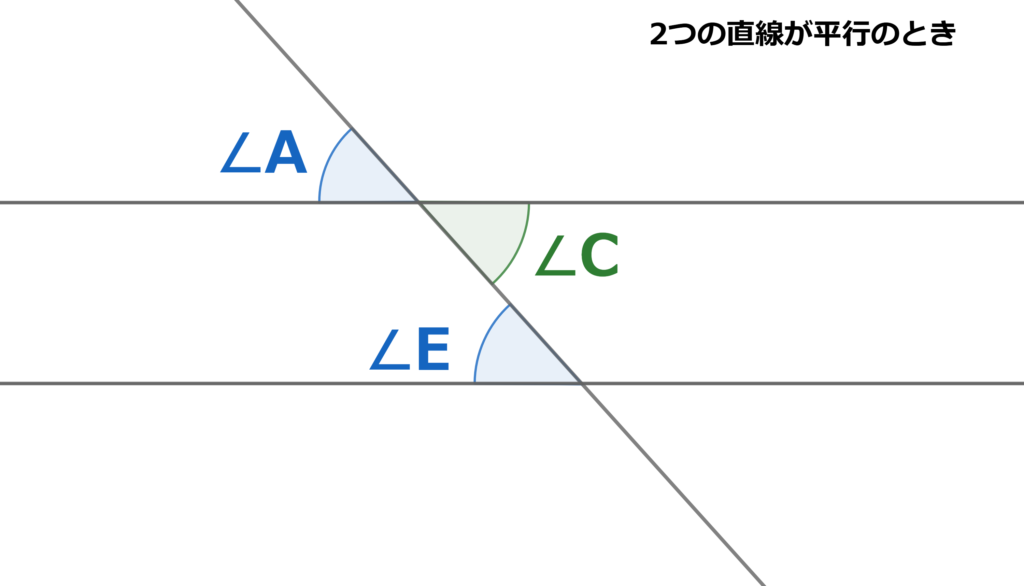
ここで$∠A$の対頂角$∠C$を考えます。
対頂角は等しいから
$∠A=∠C$
ですよね。
ということは、
$∠C=∠E$ となるわけです。
つまり、2つの直線が平行のとき錯角は等しくなるといえます。

2つの直線が平行ならば
同位角どうしは等しい大きさになる
錯角どうしは等しい大きさになる
逆に、
同位角の大きさが等しければ2つの直線は平行である
錯覚の大きさが等しければ2つの直線は平行である
ともいえるので、合わせて覚えておきましょう。
それでは例題を使ってここまでの基本をおさえておきましょう。
まとめの問題
基本例題1
直線$l,m,n$がそれぞれ並行で図のような関係があるとき、$∠A$と$∠B$の大きさを求めよ。
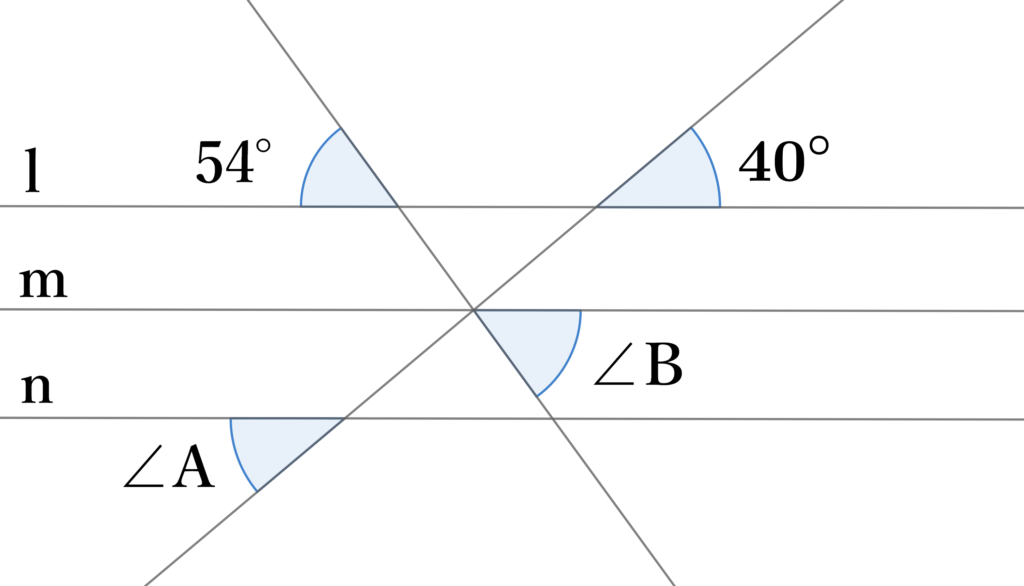
解答
ここでは対頂角、同位角を見つけていきましょう。
なお角度を求める問題ではとにかく、角度がわかる部分には図に角度を書きこむ習慣をつけておきましょう。
$∠A=40°$ $∠B=54°$
基本例題2
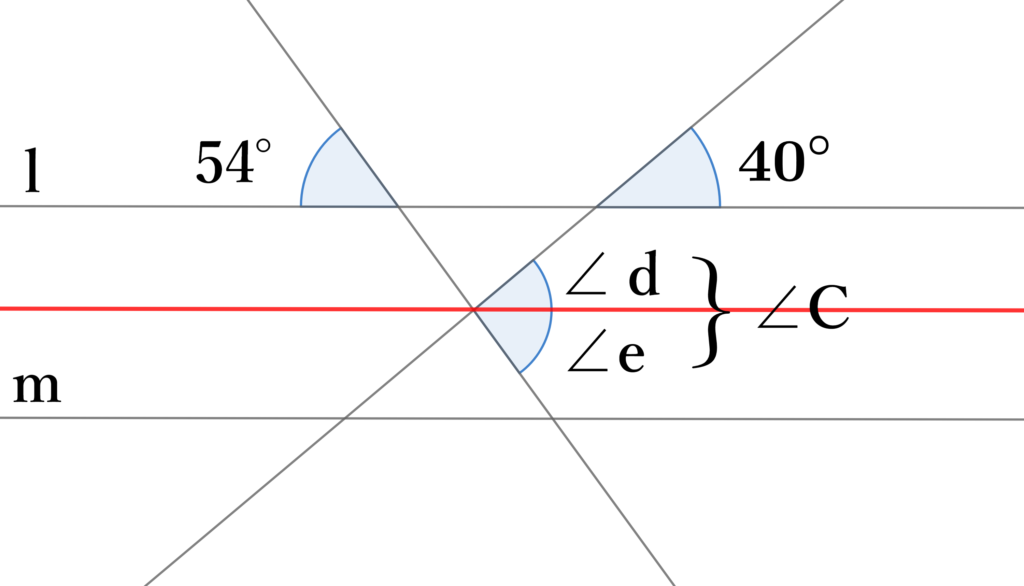
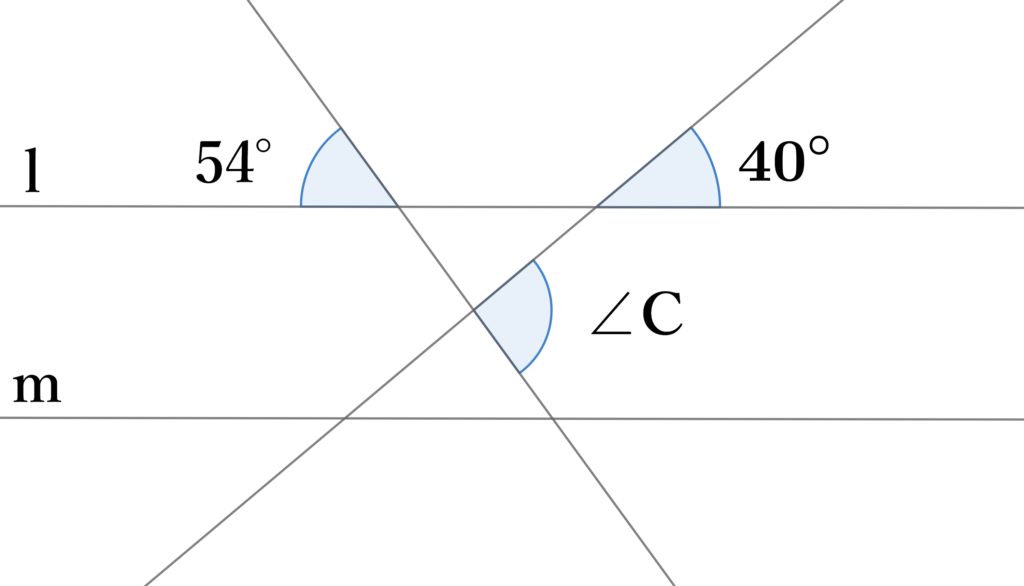
直線$l,m$がそれぞれ並行で図のような関係があるとき、$∠C$の大きさを求めよ。
考え方
基本例題1では平行線と同位角の関係を見つければ簡単に解けました。
一方この基本例題2では、求めたい部分に平行線がないので単純には求められません。
ということで一工夫します。
その工夫とはズバリ、補助線を引くこと。
実は基本例題1がヒントになってます。
解答
直線$l,m$に並行で$∠C$を通るように直線を引く。
その線を境に$∠C$を$∠d$と$∠e$に分ける。
$∠40°$の同位角が$∠d$
$∠54°$の対頂角の同位角が$∠e$
よって
$∠C=40+54=94°$