相似の基本と日常生活での利用

ここでは相似とは何かを学び、定期テストで必ず出題される相似の基本的な問題を練習します。
合わせて、日常のどのようなところに相似が利用が利用されているか理解しましょう。

相似な図形とは

相似な図形とは
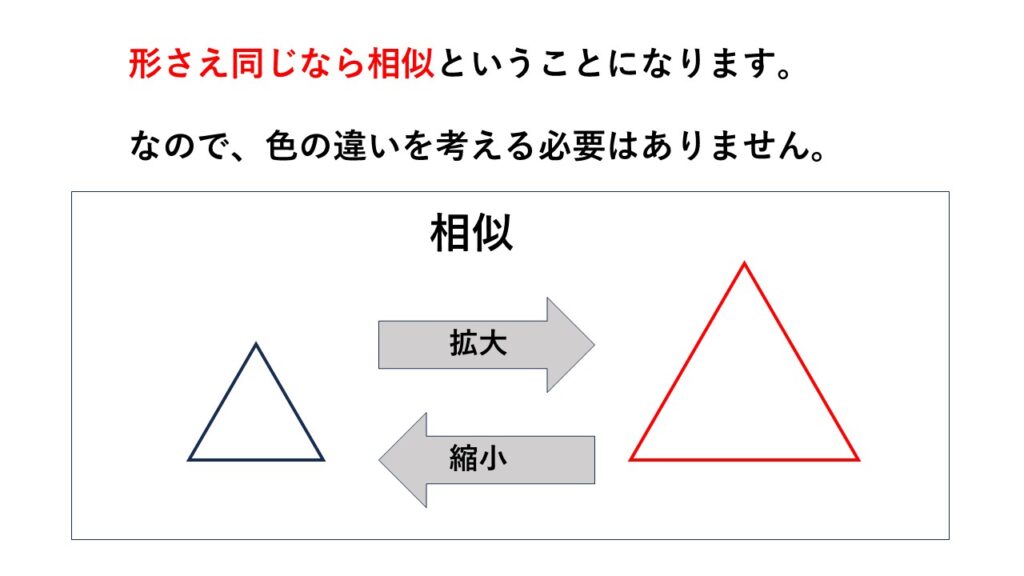
形を変えずに拡大、または縮小して得られる図形
のことをいいます。

大きさの違いを考えるというところがポイント。

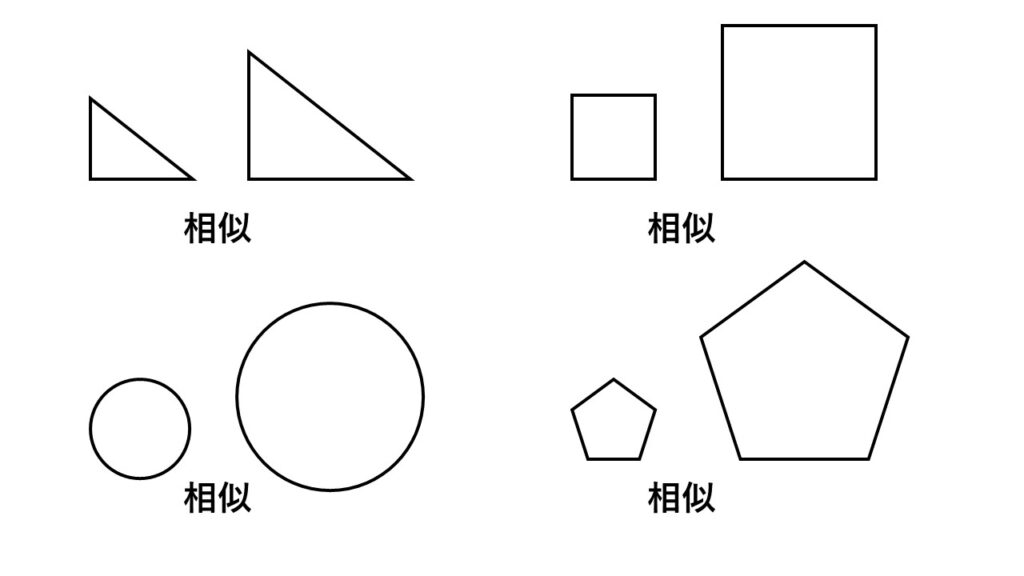
三角形に限らず四角形や五角形、円なども、形を変えずに拡大、縮小して得られれば相似の関係となります。

とにかく形と大きさに注目。
図形の中のデザインや色などは考慮しません。

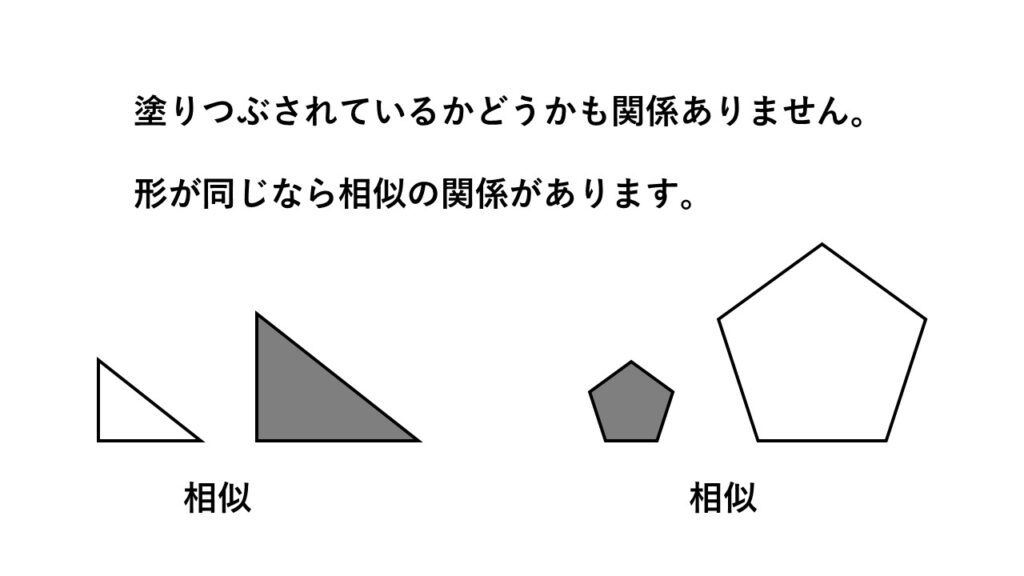
名前がないような図形でも、形はそのままで拡大縮小の関係であれば相似となります。

例えば大きい方のソーセージは小さい方をそのまま拡大したものなので、これらは相似なソーセージです。

ただ形が少しでも違うと相似とはいえません。
そのため「似ている形」では相似とはなりえません。

中2で合同というものを学習しました。
合同は形も大きさも等しい関係のことでしたね。

相似の関係のうち、偶然大きさも等しくなったものを合同と考えると良いでしょう。

合同を学んだときには三角形の合同条件を覚え証明をたくさんやりました。
正直なところウンザリだったと思います。
そして残念ながら相似でも証明問題がたくさん出てきます。ただ合同の証明に慣れていれば、相似についても実は意外とスムーズに解答できるものです。

2つの図形が相似であることを証明する。

もちろん名前のない形について証明することはありません。合同のときと同様、証明は主に三角形について学びます。

相似は新しい学習内容というよりかは、既に学習している合同をほんの少し発展させた内容ともいえます。
もちろん相似についての新しい学習内容もありますが、合同を理解していれば相似も比較的早く理解できます。
相似を勉強したら、合わせて合同も復習することをお勧めします。

相似の表し方

相似の記号

相似は記号$\quad\backsim\quad$を使って表します。

記号はSをそのまま倒した形です。

※本サイトではソフトの都合上、相似の記号が$\:\backsim\:$のように中途半端な形のＳを倒したものに見えますが、実際に書くときはイラストのようにはっきりとしたＳを倒しておくと良いと思います。

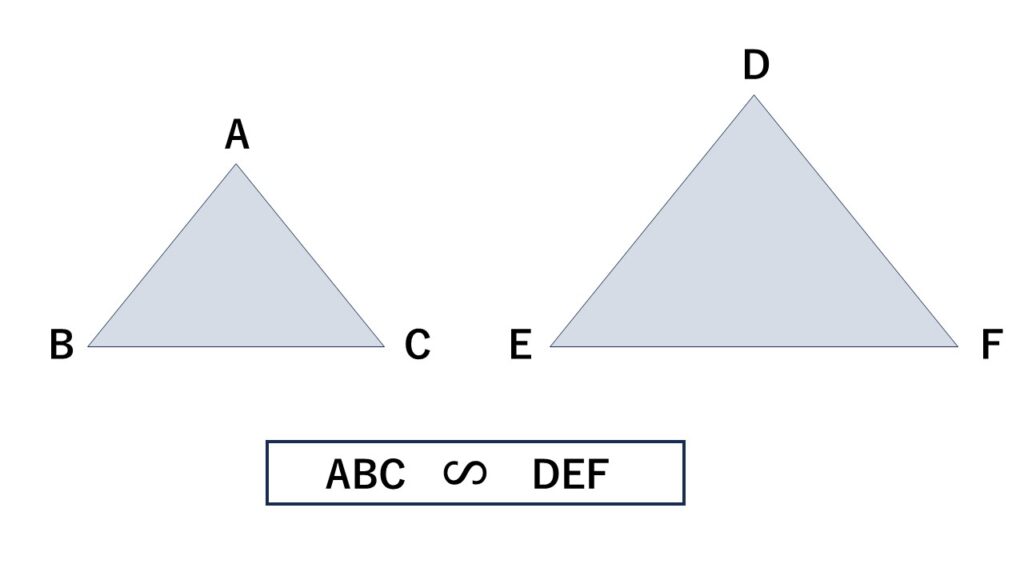
相似の関係を表すときは合同のときと同様、対応する点の順でアルファベットをかくのが基本です。

一方の図が回転していたり裏返しになっていても、相似であれば対応する順で表記します。

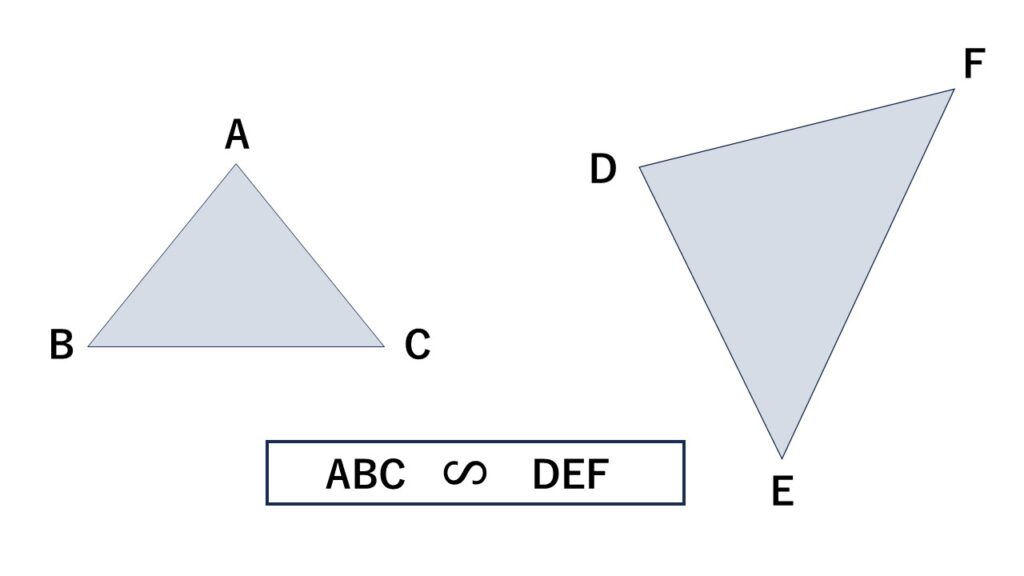
相似比とは

相似比とは対応する辺の比のことです。

相似比で表すと、どれくらいの割合で拡大もしくは縮小しているかを知ることができます。


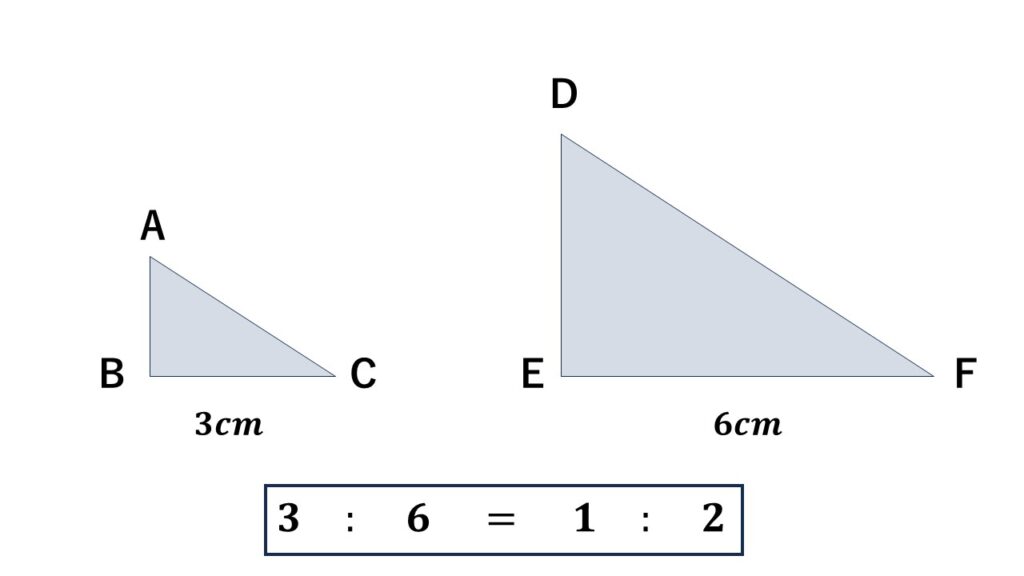
図は$\quad\triangle ABC\backsim\triangle DEF\quad$で
$BC$と$EF$が対応し長さがそれぞれ$3cm,6cm$とします。
このとき相似比は$1\;:\;2$となります。

※対応とは大きさ同じになったときにピッタリ重なる部分のこと
※合同のときの相似比は$1:1$

相似な図形を比で表す、つまりどれくらいの割合で拡大や縮小されているかは様々な所に応用が効きます。
具体的にはどのように利用されるのか見てみます。

相似の日常生活での利用

模型

模型が実物の縮小版なのは想像つくと思います。

もの凄く大きいものを作るときは模型でシミュレーションします。
逆に大きいものを小さくして楽しむこともあるでしょう。
$20m$位ある人型メカの模型は、実物を忠実に縮小しないと人型メカファンが怒ってしまいます。
相似は重要です。

デザイン

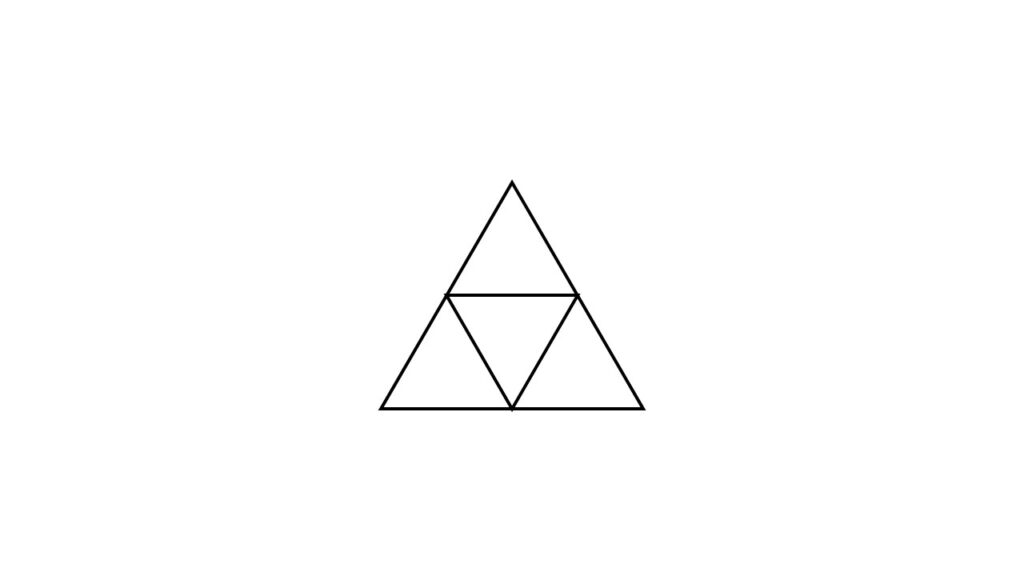
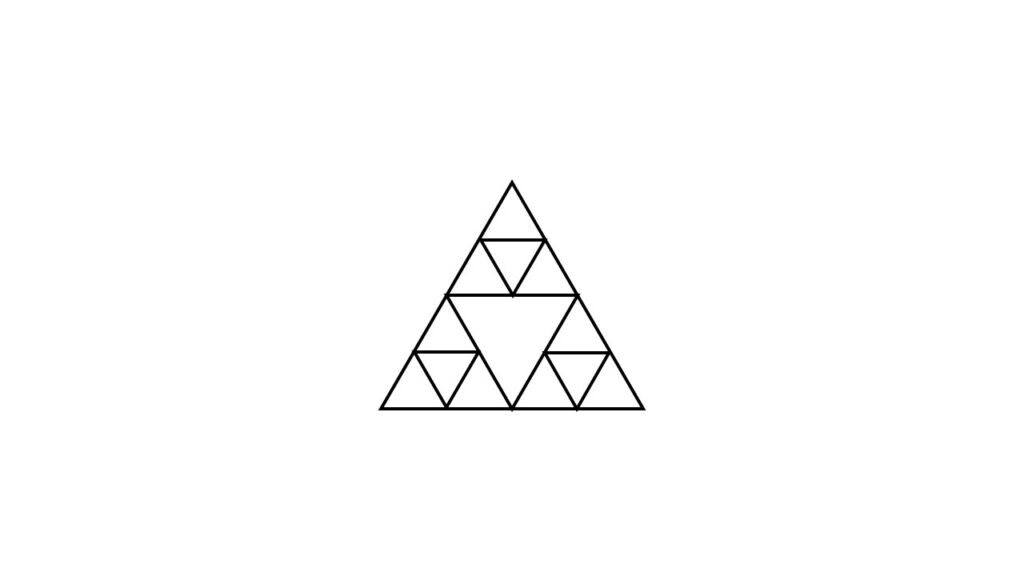
これらは1つの三角形を縮小したものをある規則に沿っていくつも並べたものです。
これと似たようなデザインの物をどこかで見たことがあるかもしれません。

もの凄く大きいものの大きさを求める

例えば特撮映画などでは巨大怪獣が出てきますが、なぜか巨大怪獣の身長が〇$m$などとわかっています。
これは怪獣に「身長計に乗ってください」とお願いして実際に計ったのではなく、周りにある建物を基に三角形の相似を応用して求めているはずです。

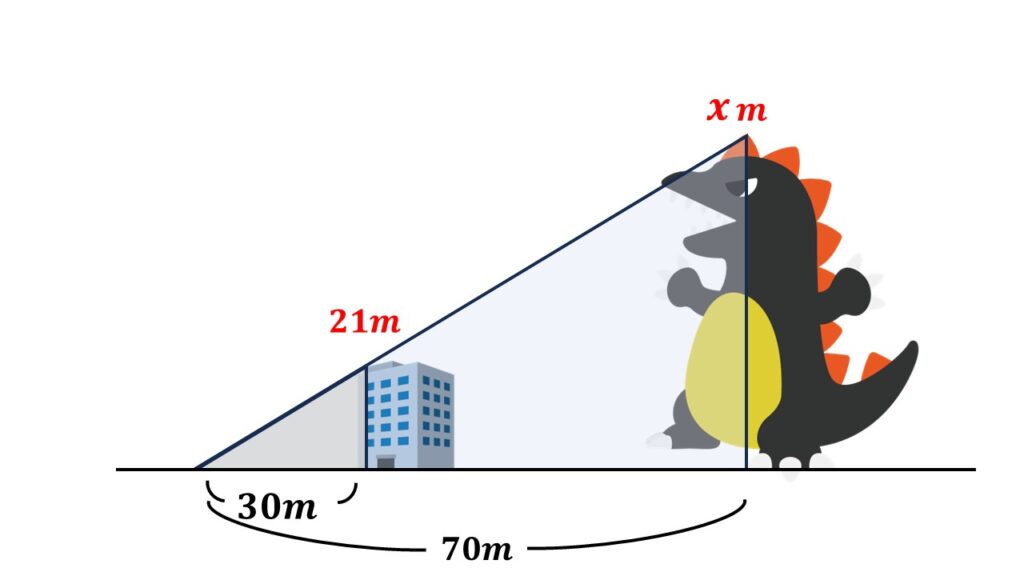
怪獣を遠目に見たとき、ある点と怪獣の足元、怪獣の頭を点で結び三角形を考えます。
それと、その三角形に中にピッタリ収まるような所に偶然、高さが$21\:m$とわかっている建物があるとします。
そしてさらに偶然が重なり、図のような位置関係ができていたとします。
すると2つの三角形を考えることができます。

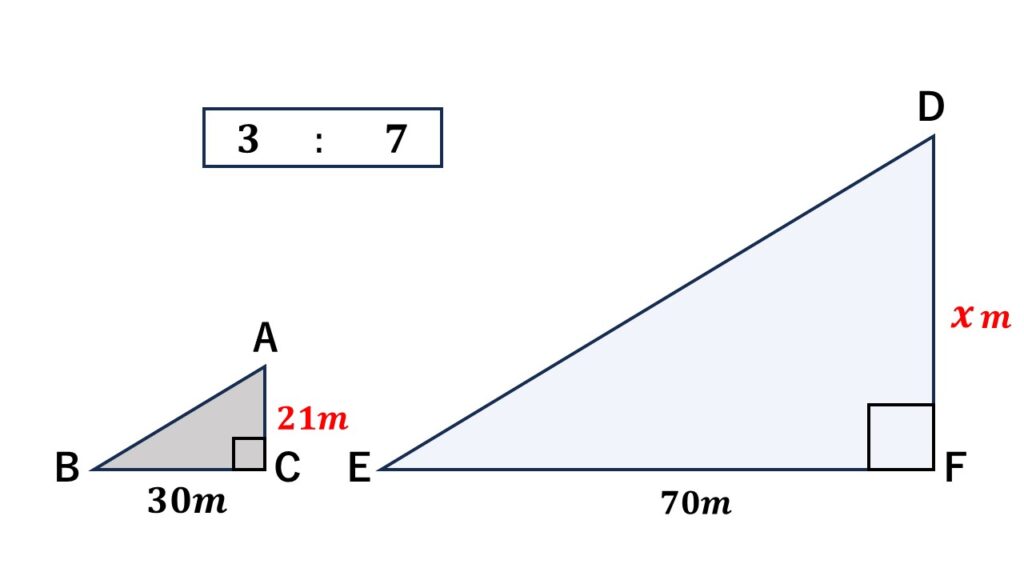
このとき2つの三角形は相似の関係にあります。（なぜ相似とわかるのかは三角形の相似条件のページを参照）
相似比は$\:30\::\:70\quad$から
$\:3\::\:7\quad$になります。

相似比がわかれば$x\:、$つまり巨大怪獣の身長を次の比例式の計算で求められます。
比例式は次の2通りの考え方がありますが、どちらも結局やってることは同じです。

日常生活ではさすがに怪獣は出てこないと思いますが、ものすごく大きいものをいったん縮小し、その中で考えるというのはよくあります。
日常生活で直接相似の計算を使うことは少なくても、そこからほんの少し踏み込めば至る所に相似の考え方は応用されています。

相似を考えるときの全ての基本は、相似比を考えるところから。
つまり比例式を使って対応する辺の長さを求められるようにすることが必須です。

次の基本例題を使って相似比を理解しましょう。

基本例題

図で$\triangle ABC\:\backsim\:\triangle DEF$とする。
$(1)\:\triangle ABC$と$\triangle DEF$の相似比を求めよ。
$(2)\:DF$の長さを求めよ。
$(3)\:\angle C$の大きさを求めよ。

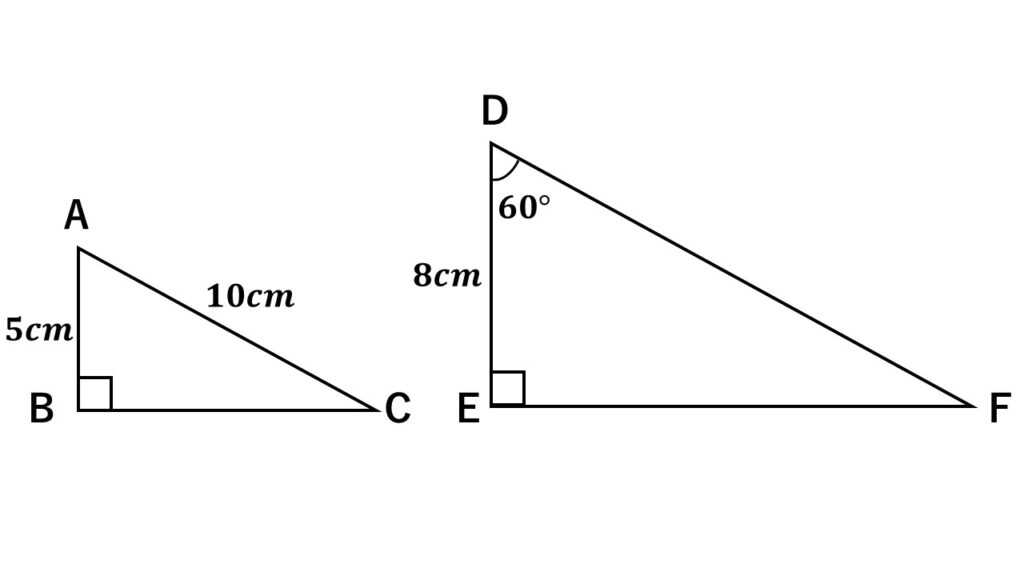
考え方
$(1)\:$対応する辺の長さに注目して比を求めます。
$(2)\:$相似比を求めて比例式を使います。
$(3)\:$相似ならば対応する角は同じ大きさです。

解答
$(1)\:5\::\:8$
$(2)\:$相似比が$5:8$なので$AC:DF=5:8$である。
$\quad\: DF$の長さを$x$とおくと
$\begin{align}\:\quad 5:8&=AC:DF\\5:8&=10:x\\5x&=80\\x&=16\end{align}$
　よって$\:DF=16\:cm$
$(3)\:30^\circ$

別解
$\begin{align}(2)\:5:10&=8:x\\5x&=80\\x&=16\end{align}$

高校入試に超頻出の相似は、相似だけを勉強していれば解答できるものではなく、中2までに学習した内容のほか、相似の後に学ぶ三平方の定理とも融合させた形で出題されます。
そのためしばしば手ごわい内容になって出題されます。

ただ相似そのものに限ってみると決して難しい内容ではありません。
そして全ての基本は、基本例題で扱った相似比を使って長さを求めるところに行きつきます。
基本例題、とくに比例式の作り方をしっかり理解しておきましょう。