三角形の相似条件を使った証明のしかた

とにかくまずは三角形の相似条件を一字一句そのまま暗記してしまいましょう。

2つの三角形があり、三角形の相似条件3つのうちのどれか1つをいえれば、その2つは相似の関係にあります。
このページでは三角形の相似条件について解説し、相似の基本的な証明問題を練習します。

三角形の相似条件が成り立つ理由

3組の辺の比がすべて等しい

参考書や問題集によっては
「3組の辺の比がそれぞれ等しい」
となっているものもありますが、どちらで覚えても問題ありません。
もちろん「すべて」が漢字で「全て」と書かれていても問題ありません。

三角形は3辺の長さが決まっていれば1つの形に決まります。

$\triangle ABC$においてそれぞれの辺の比を$a:b:c$とします。
そしてそれをそのまま形を変えずに拡大したものを$\triangle A´B´C´$とします。

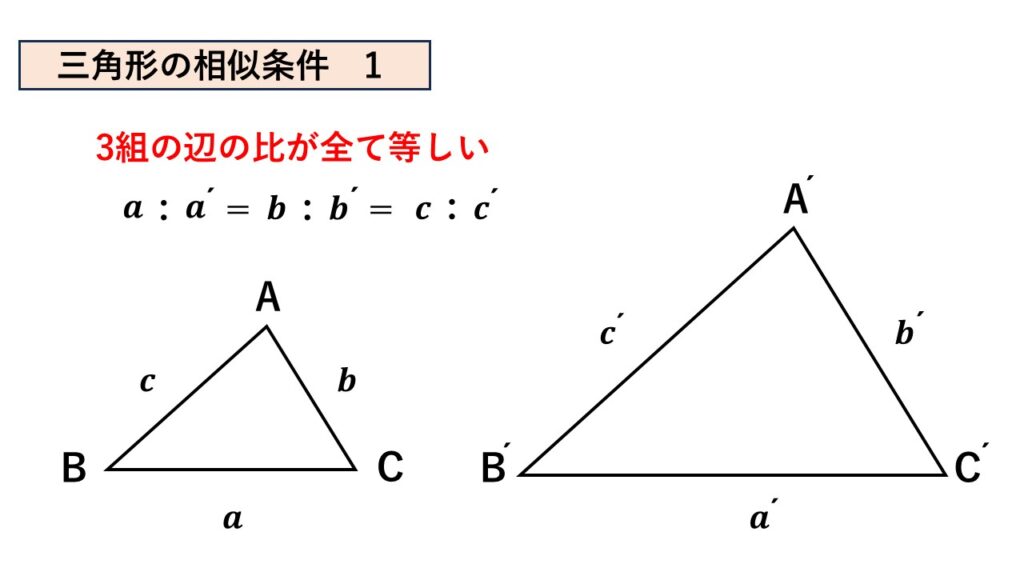
形を変えないということはつまり、$\triangle A´B´C´$の3辺の長さも決まります。
長さが決まるということは、対応する辺の比もそれぞれ変わらないということになります。
そのため$a:b:c=a´:b´:c´$となり、$a:a´＝b:b´=c:c´$といえます。

2組の辺の比とその間の角がそれぞれ等しい

辺$AB$と辺$BC$の長さが既に決まっていて、なおかつその辺にはさまれてできる角も大きさが決まっているとします。
するとそのときできる$\triangle ABC$は形状が1つに特定されます。

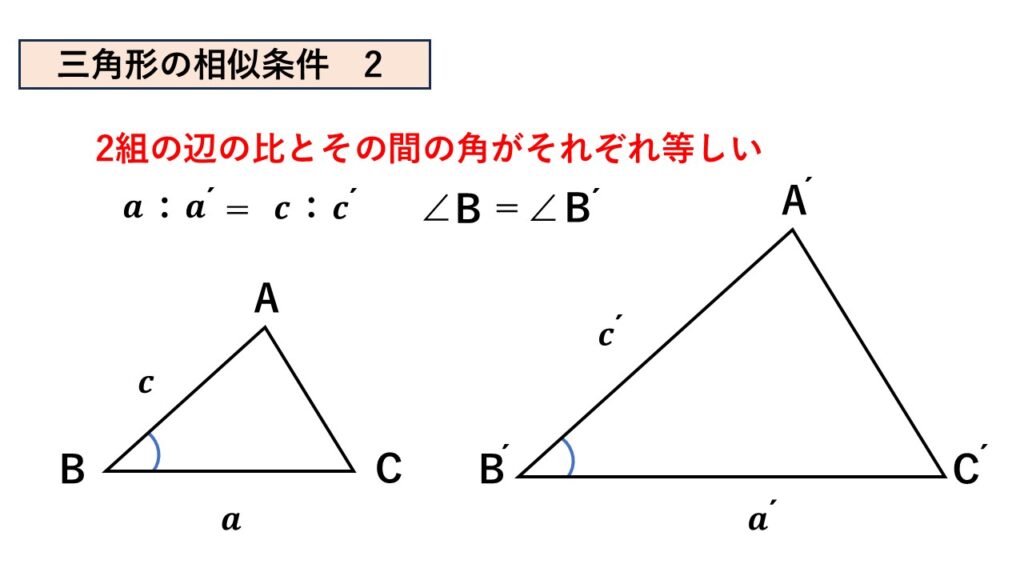
$\triangle ABC$の形状が特定されればあとは上記と同様、$\triangle A´B´C´$の3辺の長さも決まり、対応する辺の比もそれぞれ変わらないということになります。

2組の角がそれぞれ等しい

特に長さの決まってない辺$BC$があり、その両端からそれぞれ角度を決めて直線を引きます。
すると$B$を通る直線と$C$を通る直線は1か所で交わります。

その交点を$A$とすると$\triangle ABC$は形状が1つに特定されます。

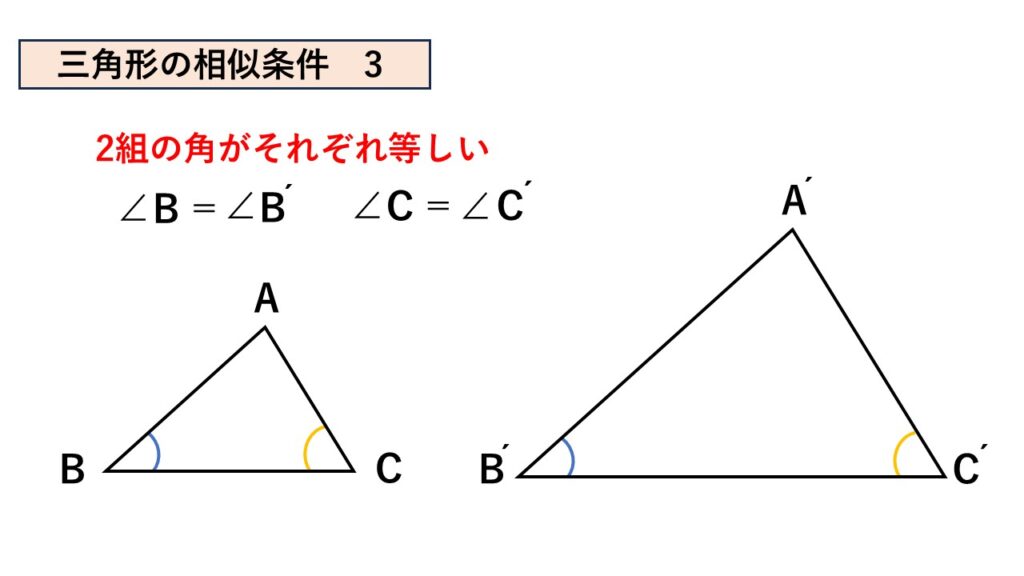
$\triangle ABC$の形状が特定されればあとは上記と同様、$\triangle A´B´C´$の3辺の長さも決まり、対応する辺の比もそれぞれ変わらないということになります。

三角形の相似条件をおさえたところで次の超基本例題に進みましょう。

超基本例題1



次の図で相似な三角形を選び記号を使って表せ。
また、そのとき使った三角形の相似条件も答えよ。

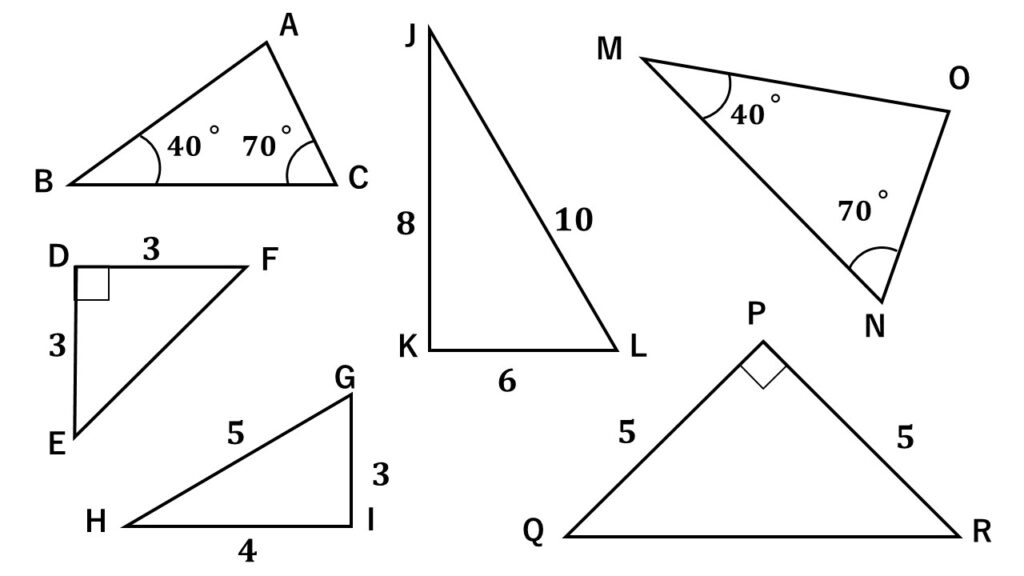
考え方
相似条件がいえそうな三角形を地道に探していきます。

解答
$\triangle ABC\backsim\triangle OMN$
2組の角がそれぞれ等しい
$\triangle DEF\backsim\triangle PQR$
2組の辺の比とその間の角がそれぞれ等しい
$\triangle GHI\backsim\triangle LJK$
3組の辺の比がすべて等しい

補足



今後学習する三平方の定理で詳しく解説しますが、
直角二等辺三角形の各辺の比は$1:1:\sqrt2$
になります。

これは覚えやすい数値の並びなのでここで暗記してしまいましょう。

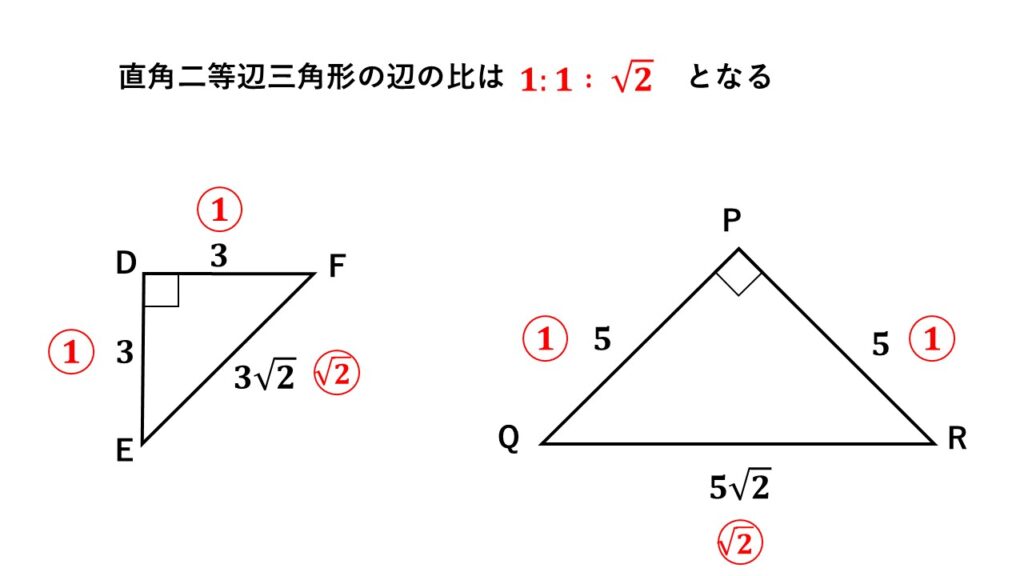
ところで超基本問題では超基本を確認するため、特にひねった問題は出しませんでした。でも直角二等辺三角形の辺の比の性質を学ぶと、

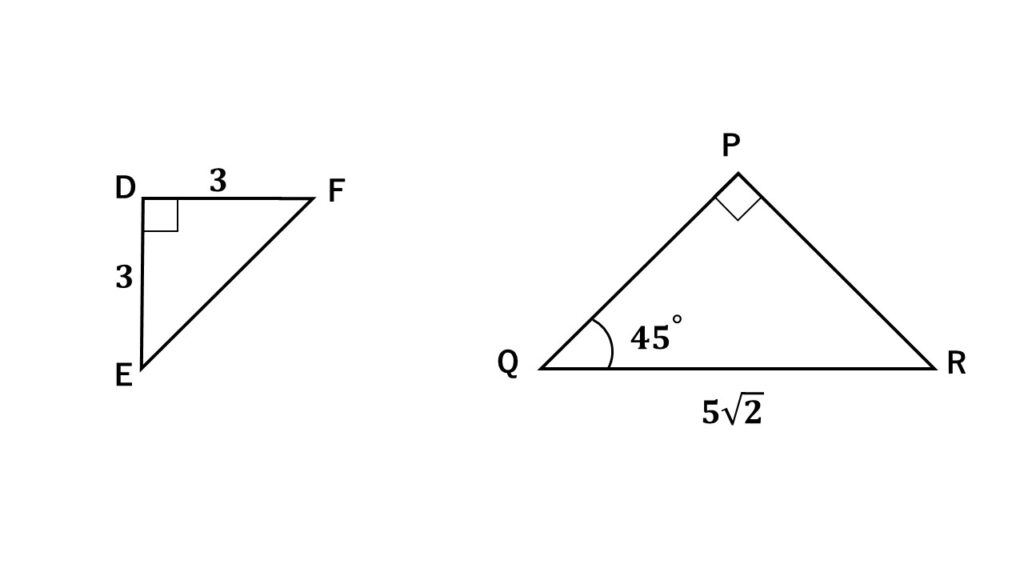
図のように、辺や角度の数値を隠した状態で二等辺三角形であることを求めさせ、相似の関係にあることを特定させる出題の仕方も出てきます。

ひねりの入った、いかにも入試に出てきそうな問題です。

別のページにも書きましたが高校入試での相似の問題は、単純に相似のみの内容としての出題はまずありません。
今まで学習してきた色々な図形の性質を合わせて考える問題がほとんどです。
忘れている図形の性質があったら、都度復習するようにしましょう。

相似の証明問題を苦手に感じてしまう理由は逆算をしないから

相似を使った証明は以下の手順にそって進めます。

三角形の相似を使った証明問題の書き方の流れ

1. 相似を証明する三角形について記す
2. 三角形の相似条件を述べる
3. だから相似だ、と結論づける

証明の流れ自体は三角形の合同を使った証明と同じで、1と2の間で相似条件を述べるための理由をあれこれ並べます。
で、ここが証明で一番苦労するところ。

ただ実際に証明する際は、頭の中では次のような思考の流れを持つようにします。

相似の証明のしかた

超基本例題2



図で$\triangle ABC$と$\triangle DEF$が相似であることを証明せよ。

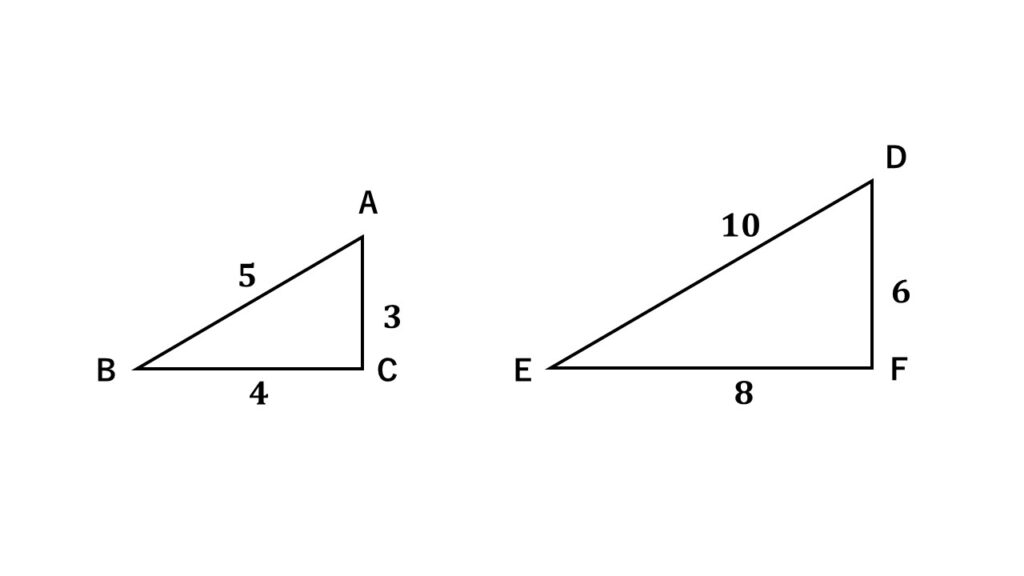
証明

補足
上記証明では三角形ごとに着目して証明を進めました。
そのため辺の比の理由説明で
$AB:BC:CA=5:4:3$
また
$DE:EF:FD=10:8:6$より
$DE:EF:FD=5:4:3$　としました。

一方、次のように対応する辺ごとに着目して証明することも可能です。

証明
$\triangle ABC$と$\triangle DEF$において
$AB:DE=1:2$
$BC:EF=1:2$
$CA:FD=1:2$
よって3組の辺の比がすべて等しいので
$\triangle ABC\backsim\triangle DEF$
証明終わり

超基本例題2では証明の流れをおさえてもらうためにごく単純な出題にしました。
でも当然テスト、こと入試ではここまで単純な証明問題は出題されません。
次に教科書や問題集によくある、ほんの少しひねりを加えた図形で証明の練習をしましょう。

基本例題1

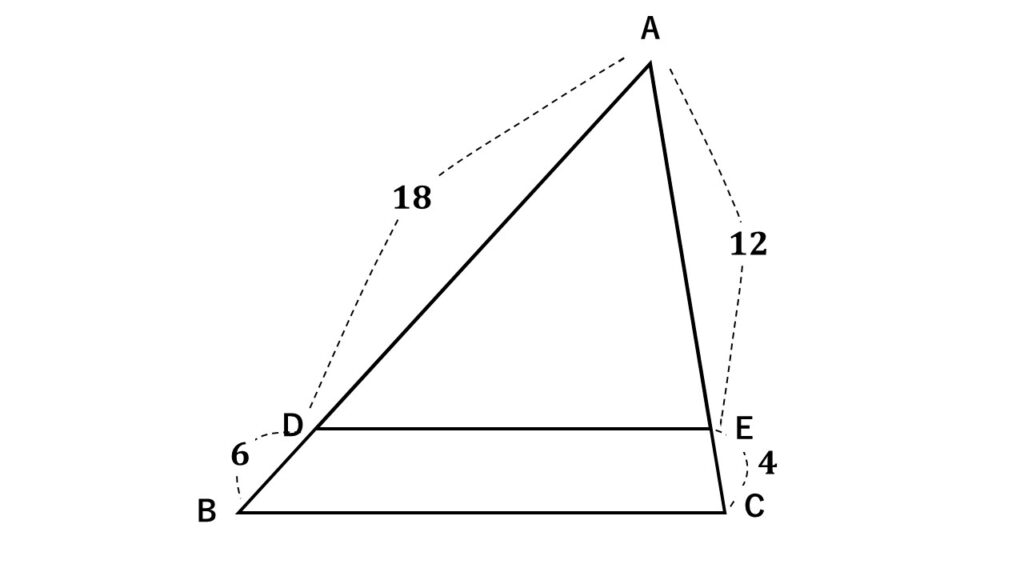
図で$\triangle ABC\backsim\triangle ADE$であることを証明せよ。

考え方
図を見て何の方針もなく証明を書くのではなく先に、いえそうな相似条件の見当をつけます。
証明を始める前の頭の中での思考は次の通り。

いえそうな相似条件は何か？
　　↓
手がかりは辺の比だけ
　　↓
他に手がかりはないか？
　　↓
$\angle A$に注目すると、$\triangle ABC$と$\triangle ADE$の2つに共通した角になっている
　　↓
しかも$\angle A$は2辺の間の角
　　↓
相似条件をいえる

相似条件の見当がついたら上記POINTの流れに沿って証明を進めます。

証明

補足
三角形ごとに注目して
$AB:AC=3:2$
$AD:AE=3:2$　を示し
2組の辺の比とその間の角がそれぞれ等しいとしてもかまいません。

続けてもう1つよくある図で証明の練習をしましょう。

基本例題2


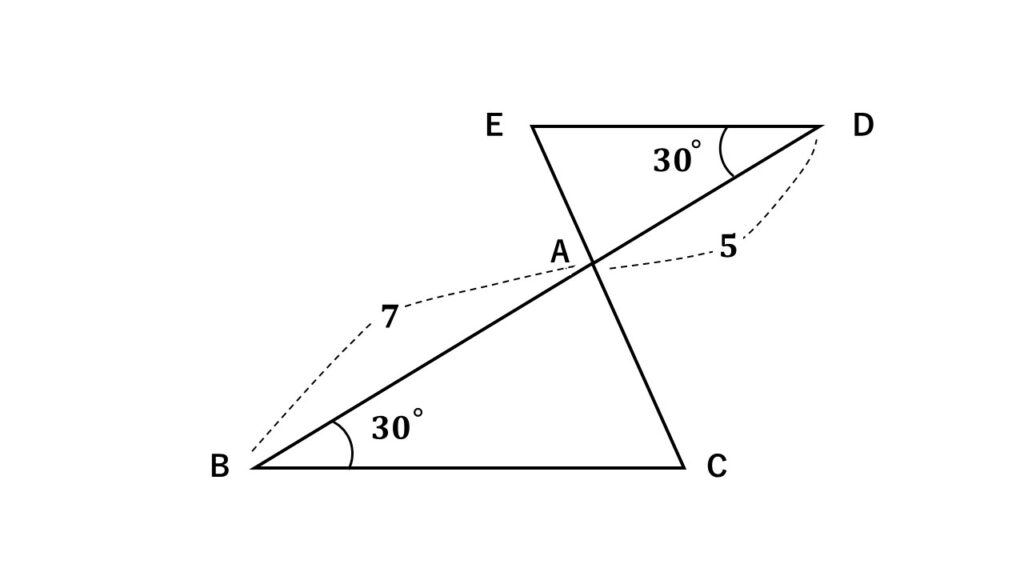
図で$\triangle ABC\backsim\triangle ADE$であることを証明せよ。

考え方
先にいえそうな相似条件の見当をつけます。
証明を始める前の頭の中での思考は次の通り。

$30$°が2か所にある
　　↓
$\angle EAD$と$\angle CAB$は対頂角になっている
　　↓
あ、この時点で相似条件をいえる
　　↓
ってことは辺の比$7$と$5$は証明に必要ないじゃん

補足
この例題では、辺の比は相似の証明には必要ありませんでした。
目についたものをやみくもに並べて証明を進めようとすると、必要のない$7$と$5$に惑わされて証明が進まなくなります。
このように、先にいえそうな相似条件の見当をつけ、逆算して考えることの大切さもわかるかと思います。
特に複雑な図の証明では、逆算思考を常に念頭に入れておきましょう。

なおこの基本例題2、次のようような証明も可能です。

基本例題2　別解

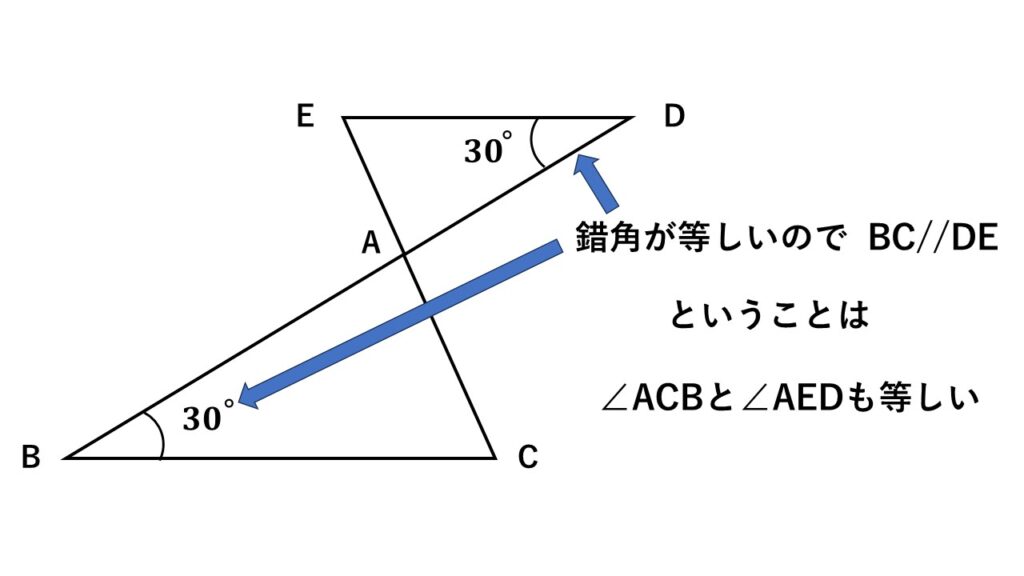
$\angle ABC=\angle ADE$で錯角が等しくなっているので、$BC//DE$がいえます。
ということは$\angle ACB$と$\angle AED$も平行線と錯角の関係から等しくなります。
これより
2組の角がそれぞれ等しい
として証明することも可能です。