
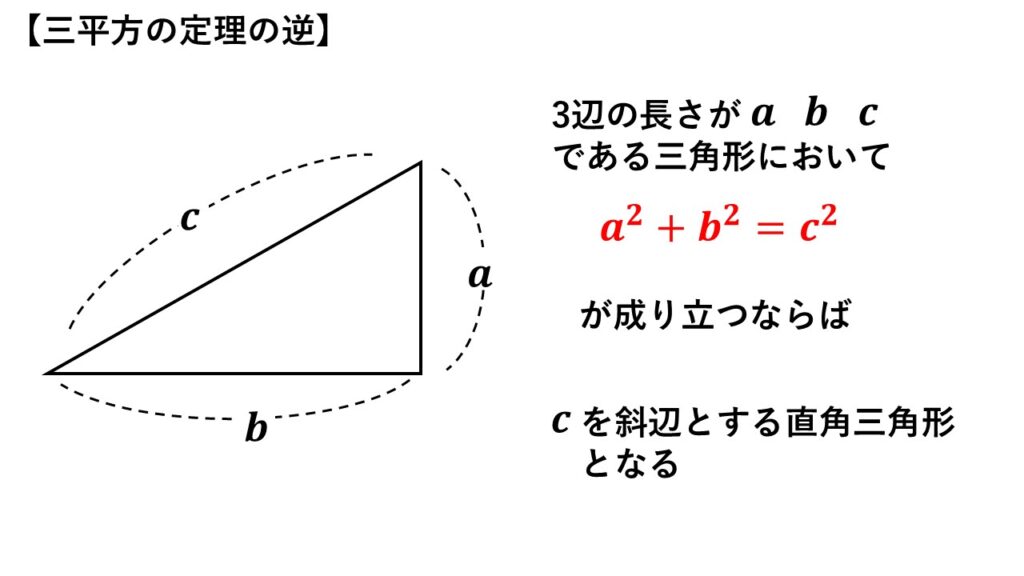
三平方の定理の逆
3辺の長さが$a,b,c$である三角形において
$a^2+b^2=c^2$
が成り立つならば
その三角形は$c$を斜辺とする直角三角形となる
いきなりPOINTから入りましたが、これだけ見ると
「三平方の定理と三平方の定理の逆とは何が違うの?」と感じたかもしれません。
この三平方の定理の逆もとても重要な内容。基本中の基本をしっかり理解していきましょう。
$a^2+b^2=c^2$の関係があるから直角三角形となる
ざっくり言ってしまえば、三平方の定理は
直角三角形ならば$a^2+b^2=c^2$となる というものでした。
そして三平方の定理の逆はまさにその逆、
$a^2+b^2=c^2$ならば直角三角形となる というものです。
つまり3つの辺の長さが与えられたときに、
$a^2+b^2=c^2\:$
の計算式が成り立てば、その三角形は直角三角形であることが計算で断定できるというもの。
それでは具体的にどのような形で問題が出てくるのか。
基本例題を使って三平方の定理の逆について練習です。
基本例題1
各辺の長さがそれぞれ次のようになっている三角形のうち、直角三角形であるものを選べ。
$(1)\:1\:cm\quad 3\:cm\quad 6\:cm$
$(2)\:1\:cm\quad 2\:cm\quad \sqrt5\:cm$
$(3)\:3\:cm\quad 5\:cm\quad 7\:cm$
$(4)\:7\:cm\quad 24\:cm\quad 25\:cm$
考え方
三平方の定理の逆を使います。
つまり一番大きい数の2乗が他の2数の2乗の和に等しいかどうかを確かめます。
解答
$(1)\:1^2+3^2=10\quad 6^2=36$
よって直角三角形ではない
$(2)\:1^2+2^2=5\quad (\sqrt{5})^2=5$
よって直角三角形となる
$(3)\:3^2+5^2=34\quad 7^2=49$
よって直角三角形ではない
$\begin{align}(4)\:&7^2+24^2=49+576=625\\&25^2=625\end{align}$
よって直角三角形となる
解説
三平方の定理の逆は、主に直角三角形であることを確認するために使います。
そして三平方の定理の逆を使って直角三角形かどうかを求める問題は、1つ1つ丁寧に計算して確認するしかありません。
当然一番大きい数値が直角三角形の斜辺に該当します。
基本例題1では基本を身につけるために比較的簡単な数値での出題にしました。
ただ実際のテストでは小数や分数、根号のついた数などでの出題もあるはずです。
数値の大小関係で間違うことのないよう気をつけましょう。
特に根号のついた数値の大小関係に注意が必要です。
三平方の定理の証明と三平方の定理の逆の証明
※ 中学レベルでは三平方の定理の逆はその性質を覚えておけば十分で、証明までできる必要はありません。
つまり基本例題1ができれば十分です。
一歩踏み込んで学びたい人は読み進めてください。
ある定理が成り立つなら、その逆も考えるようにする。そして逆は必ずしも正しいとは言い切れないから、正しいかどうかの確認が必要だ。
同様なことを別のページでも書いていますが、三平方の定理の逆もまたしかり。
ということで、三平方の定理の逆がどうして成り立つのかについて証明していきます。
ですがその前にそもそも、
どうして三平方の定理が成り立つのか
を示さないと、三平方の定理の逆の証明が不十分になってしまいます。
そのため先に三平方の定理が成り立つことを証明し、そのあと三平方の定理の逆の証明をしていきます。
なぜ三平方の定理が成り立つのか
三平方の定理は様々な方法で証明できますが、ここでは正方形の面積に焦点を当てた方法で証明します。
三平方の定理の証明なので、
直角三角形ならば$a^2+b^2=c^2$が成り立つ
ことの証明です。
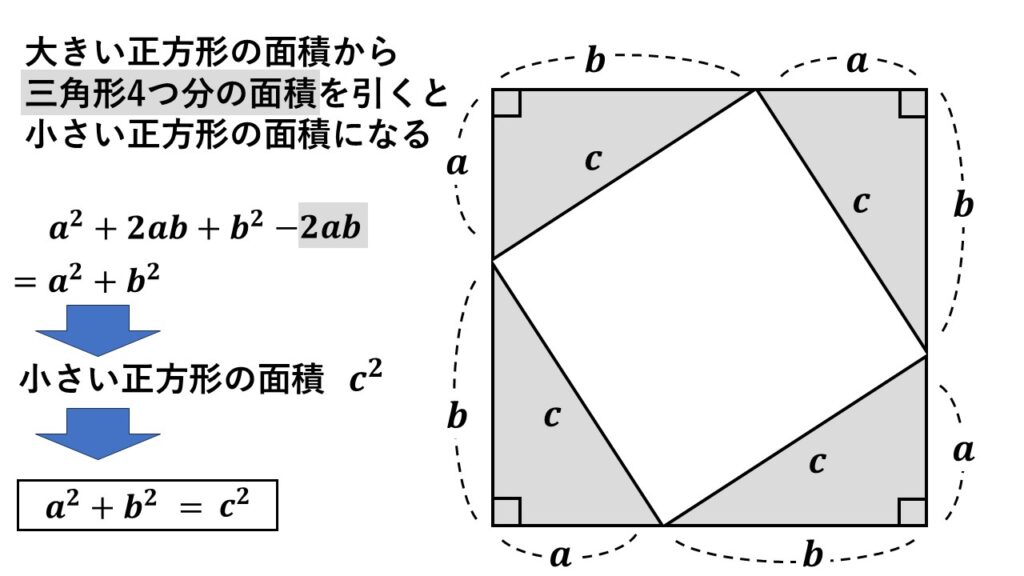
【証明】
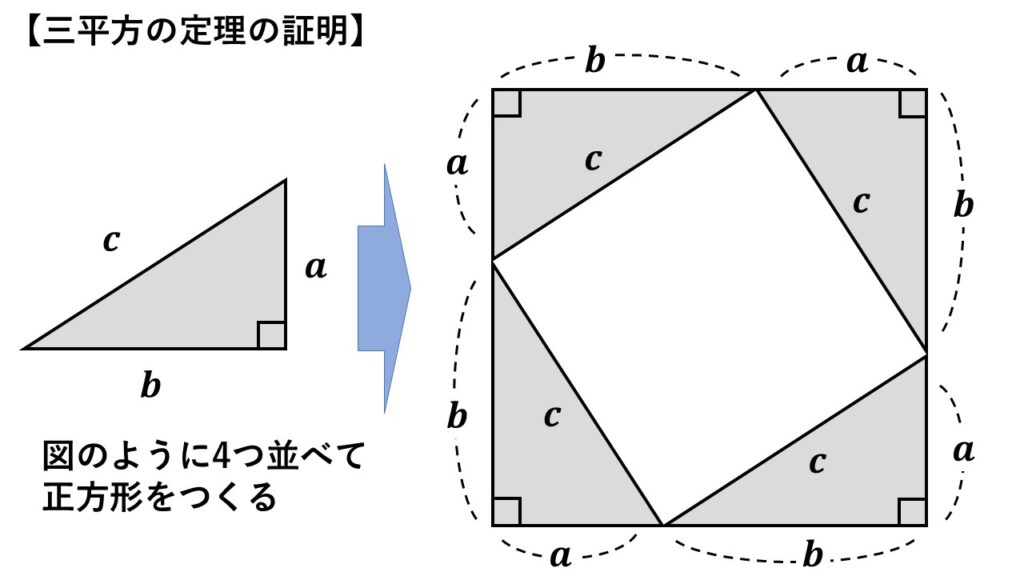
3辺がそれぞれ$\:a,b,c\:$とする三角形で、斜辺を$c$とする直角三角形を考える
その直角三角形を、図のように大きな正方形ができるように4つ並べる
すると
大きな正方形の1辺は$\:(a+b)$
小さな正方形の1辺は$\:c$
とおける
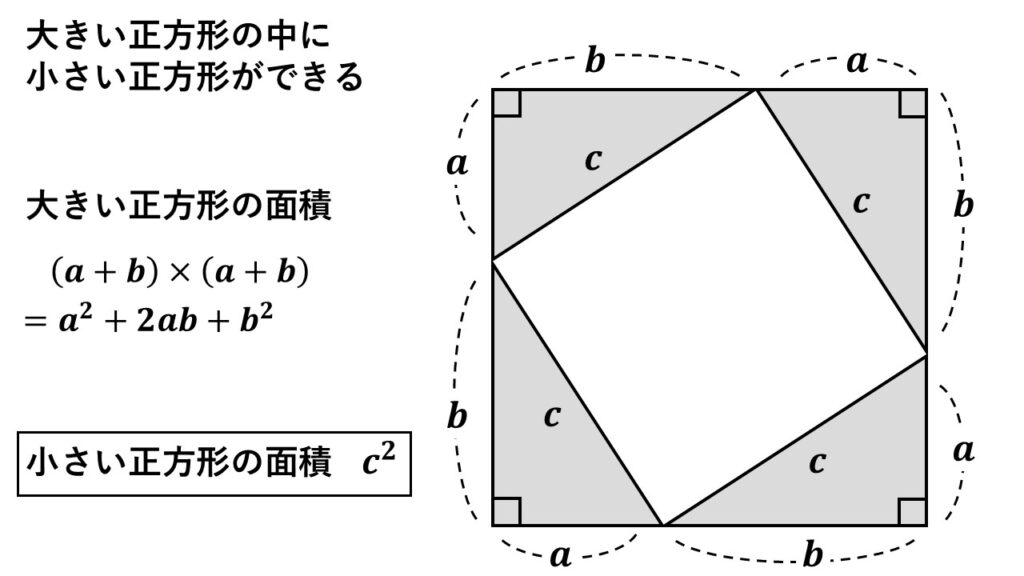
このとき大小それぞれの正方形の面積を表すと
大きいほうの正方形は
$\begin{align}&(a+b)\times(a+b)\\=&a^2+2ab+b^2\quad①\end{align}$
小さいほうの正方形は
$c^2$ となる
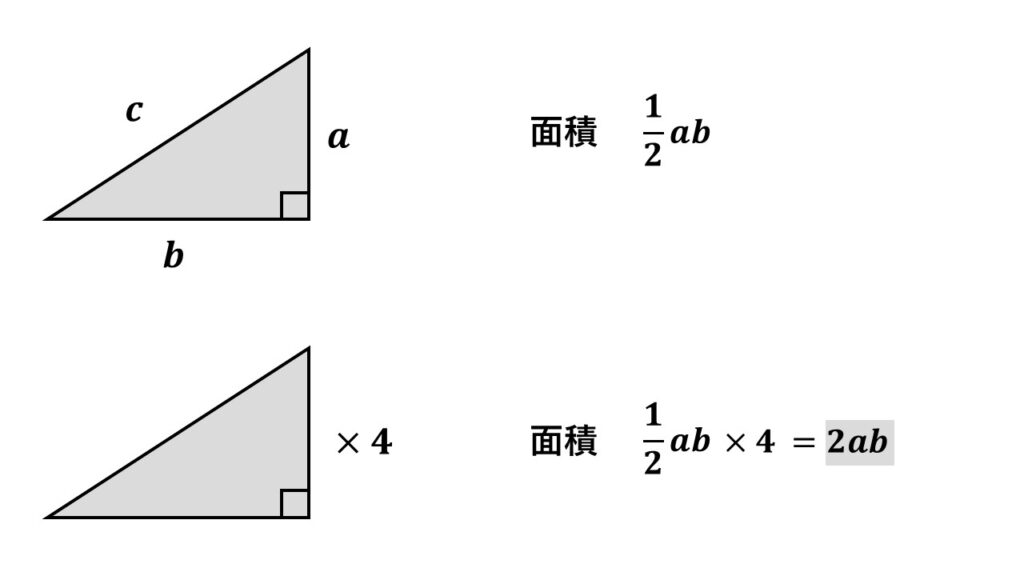
ここで直角三角形1つの面積は
$\dfrac{1}{2}ab$ となるので
直角三角形4つ分の面積は
$\dfrac{1}{2}ab\times4=2ab\quad②$
となる
大きい正方形から
直角三角形4つ分を引いたものが
小さい正方形の面積なので
①$\:-\:$②より
$\begin{align}&(a^2+2ab+b^2)-2ab\\=&a^2+b^2=c^2\end{align}$
したがって
3辺がそれぞれ$\:a,b,c\:$で斜辺を$c$とする直角三角形では
$a^2+b^2=c^2\:$となり
三平方の定理が成り立つ
【証明終わり】
解説
三角形を4つ集めて正方形を作り、そこからさらに面積を求めて引いたりと、初見には難易度高めの内容でした。
そもそも正方形を作るという発想自体がなかなか出てこないと思います。
面積を考えてそこから計算上$\:a^2+b^2=c^2\:$が求まる。
この程度に軽く覚えておけば十分です。
続いて三平方の定理の逆の証明です。
三平方の定理の逆の証明
$a^2+b^2=c^2\:$ならば直角三角形だ
の証明。ここでは、
3辺の長さがわかっているけど形状が不明確な三角形と
斜辺の長さはわからないけど確実に直角三角形とわかっている三角形
の2つの三角形を比較して証明します。
証明の大まかな流れとしては、
形状が不明確な三角形に対し$a^2+b^2=c^2$が成り立っていると仮定します。
そして、それと比較するために確実に直角三角形と分かっている三角形を1つ使い、計算上で2つの三角形が合同であることを示します。
つまり形状が不明確な三角形は直角三角形であったことを示します。
結果として$a^2+b^2=c^2$の関係が成り立てば直角三角形にしかならないことを導きます。
【証明】
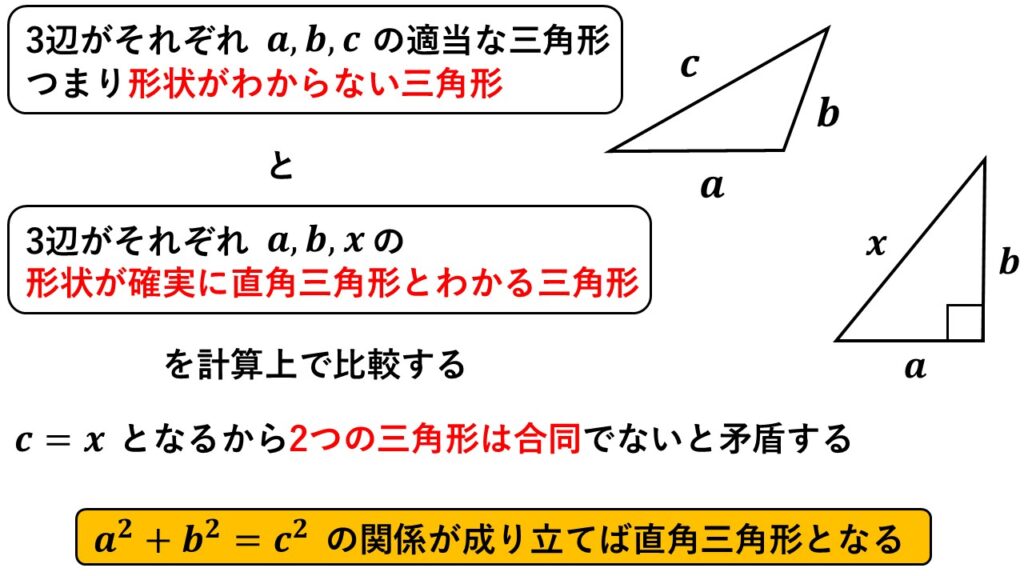
3辺がそれぞれ$\:a,b,c\:$で$a^2+b^2=c^2\:$が成り立つ三角形をつくる
また2辺がそれぞれ$a,b$でその間の角が$90°$、残りの1辺が$x$である直角三角形をつくる
直角三角形には三平方の定理が成り立つので
$a^2+b^2=x^2\quad$
ここで
$a^2+b^2=c^2\:$と
$a^2+b^2=x^2\:$より
$c^2=x^2$
$c,x$は三角形の辺なのでそれぞれ$\:c>0,x>0$
よって$\:c=x$
したがって2つの三角形は$a=a,b=b,c=x$から3組の辺がそれぞれ等しいので合同である
このことから3辺がそれぞれ$\:a,b,c\:$の三角形は$a,b$の間の角が$90°$の直角三角形といえる
以上より
$a^2+b^2=c^2$が成り立てば$c$を斜辺とする直角三角形になるといえる
【証明終わり】
解説
三平方の定理の逆の証明をするのに、その途中で三平方の定理が出てきました。
そこに疑問を持った人もいると思います。
「三平方の定理の逆を証明するのに三平方の定理を使ったら、証明が堂々巡りして証明にならないのでは?」と。
確かに、直角三角形だと証明したい3辺$\:a,b,c\:$の三角形に対して、直接三平方の定理の逆を使ってしまうと堂々巡りになってしまいます。
その疑問に予め答えるために三平方の定理の証明をしました。
三平方の定理の証明は正方形の面積を根拠としています。
正しいものと証明したので、三平方の定理自体は別の定理の証明の根拠として使えます。
つまり直角三角形とわかっているものに対して、三平方の定理を使うことができるようにしました。
そして三平方の定理の逆の証明では、3辺$\:a,b,c\:$の三角形とは別の三角形(斜辺$\:x\:$の直角三角形のこと)に対し、$\:x\:$の性質について三平方の定理を根拠として論じています。
そのため証明の堂々巡りには当たりません。
AばらばBの逆 BならばA が正しいと断言できるのはどんなときか?
逆の証明は結構難しいです。
突然ですが例えば、
東京都の中に足立区という区があります。
さらに足立区の中には舎人という地区があります。
そのため
「舎人に住んでいれば足立区に住んでいる」
とは間違いなく断定できます。
ならば逆に
足立区に住んでいれば舎人に住んでいる
といえるか?
というと、そうとはいえません。
足立区の中には舎人の他に、谷在家、鹿浜、伊興、古千谷、六月、花畑・・・など多くの地区があります。
一般的に
A ならば B という文脈があったとき、
AよりもBのほうが広いものならその文脈は正しくなります。
でもAのほうが広くBが狭い範囲を示しているなら、それは正しいと言い切れなくなります。
すると、AならばBが正しくて、その逆 BならばAも確実に正しいと断言できるのはどんなときかというと、A=Bのとき(もう少し正確に言うと、Aに含まれる要素とBに含まれる要素が完全一致するとき)になります。
なので、足立区に住んでいれば舎人に住んでいるというのは正しいとは言い切れないわけです。
(もし仮に足立区の中には舎人地区しかないなら、足立区に住んでいれば舎人に住んでいるというのは正しいことになります。)
ここで三平方の定理の逆に話を戻します。
直角三角形ならば$a^2+b^2=c^2\:$をみたす が正しくて
その逆
三角形が$a^2+b^2=c^2\:$をみたすならば直角三角形 も確実に正しいと断言できるのは
「$a^2+b^2=c^2\:$の関係式$c$」と「直角三角形の$x$」が等しいもの と示せたときになります。
この関係を示すために
「形状がわからないけど$a^2+b^2=c^2$が成り立つ三角形」 と
「確実に直角三角形と分かっている三角形」 を使い
計算上で等しいことを示したわけです。
