今まで三角形について様々なものを学んできました。
その中でも特に直角三角形については、超ウルトラスーパーハイパー級に重要な必ず覚えておくべき性質があります。
それが三平方の定理(ピタゴラスの定理)。
とても重要なだけにこのページでは、三平方の定理(ピタゴラスの定理)の基本のみを徹底して学習します。
三平方の定理

直角三角形において
斜辺の長さを$c$、残りの2辺の長さを$a,b$とすると
$\quad a^2+b^2=c^2\quad$
の関係が成り立つ
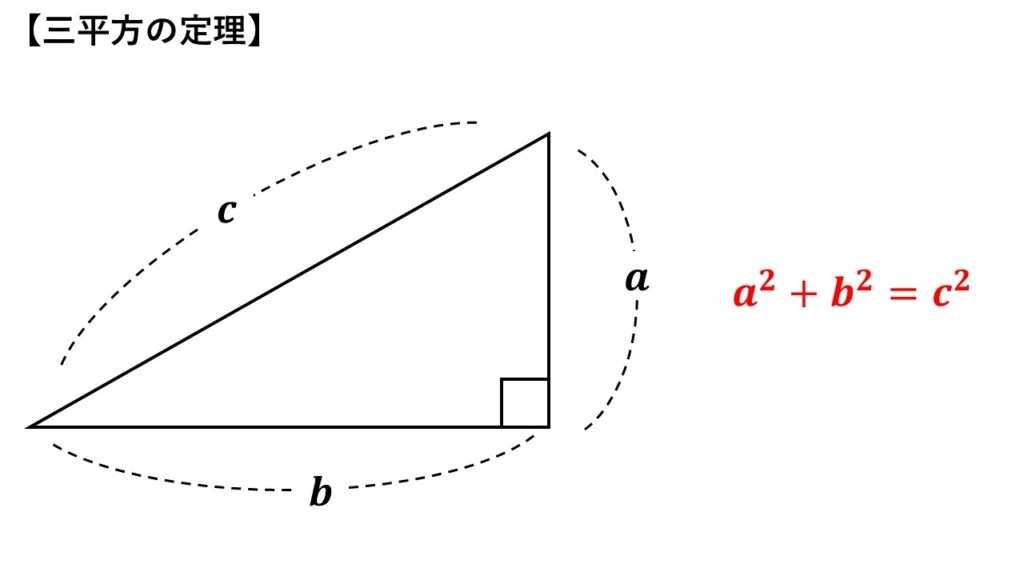
この三平方の定理は、直角三角形に限ってのお話です。
そのため直角三角形以外の三角形について$a^2+b^2=c^2$の関係を使おうとしても使えません。
このことをしっかり押さえておきましょう。
それではさっそく三平方の定理に慣れるための基本例題に入ります。
基本例題1
次の $(1)~(4)$ の図で、$c\:$の長さを求めよ。


考え方
直角三角形であることを確認して三平方の定理を使います。
$a^2+b^2=c^2$
この関係を日本語に翻訳すると
「斜辺の長さの2乗は他の2辺の長さの2乗の和に等しい」です。
$(4)$に注意しましょう。
解答
$\begin{align}(1)\:1^2+2^2&=c^2\\5&=c^2\\c&=\pm\sqrt5\end{align}$
$\quad c$は辺の長さなので$\:c>0$
よって$\:c=\sqrt5$
$\begin{align}(2)\:2^2+3^2&=c^2\\13&=c^2\\c&=\pm\sqrt{13}\end{align}$
$\quad c$は辺の長さなので$\:c>0$
よって$\:c=\sqrt{13}$
$\begin{align}(3)\:(\sqrt2)^2+(\sqrt3)^2&=c^2\\2+3&=c^2\\5&=c^2\\c&=\pm\sqrt5\end{align}$
$\quad c$は辺の長さなので$\:c>0$
よって$\:c=\sqrt5$
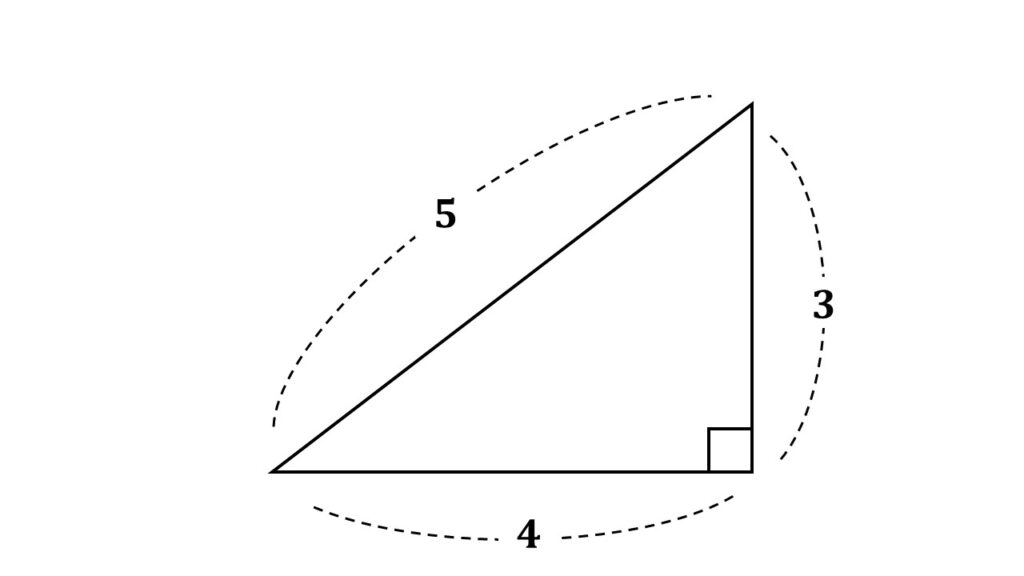
$\begin{align}(4)\:c^2+4^2&=5^2\\c^2+16&=25\\c^2&=9\\c&=\pm3\end{align}$
$\quad c$は辺の長さなので$\:c>0$
よって$\:c=3$
解説
三平方の定理は
「斜辺の長さの2乗は他の2辺の長さの2乗の和に等しい」です。
基本例題1はどれも三平方の定理をそのまま使えば解けます。
ただ$(4)$は注意。
これは斜辺の長さが分かっていて、一番短い辺の長さが分かっていませんでした。
そのため
$c^2+4^2=5^2$の式になっています。
ところで$(4)$は辺の長さが短い順に$3,4,5$となっていますね。
この直角三角形は辺の並びとして覚えやすいので、このまま暗記してしまいましょう。
三平方の定理から覚えておくべき辺の比
「$3,4,5$の辺の並びの直角三角形は覚えやすいから暗記」と書きましたが、ほかにも暗記しておいて損はない直角三角形があります。
それぞれの直角三角形について、辺の比が短い順に覚えると良いでしょう。


直角二等辺三角形

$30°,60°,90°$の三角形
4つ挙げましたが、それぞれ$a^2+b^2=c^2$の式に当てはめて計算してみましょう。
確かに三平方の定理に当てはまっていることがわかります(もし計算が合わないならどこかで計算が間違っている)。
これらの直角三角形は入試等々でよく出題されますし、高校数学でも当たり前のように出てきます。
比較的簡単な数値の並びなので暗記しやすいと思いますし、暗記しておけば時間も節約できます。
特に直角二等辺三角形($45°,45°,90°)$と$30°,60°,90°$の三角形は、三角定規に使われている重要な三角形です。
それぞれ辺の比が短い順に
$1:1:\sqrt2$
$1:\sqrt3:2$
となります。
この2つについては、角の大きさを示されたら反射的に辺の比の関係を思い浮かべられるようになっているのが望ましいです。
それでは上記4つの三角形を使った練習に進みましょう。
基本例題2
次の $(1)~(4)$ の図で、$c\:$の長さを求めよ。


考え方
直角三角形であることを確認して三平方の定理を使い計算します。
ですが、暗記しておくと良い三角形の辺の比の関係に気づければ、$\:a^2+b^2=c^2\:$の計算をしなくても相似の関係から瞬時に解答できます。
どういうことか?
しばらく考えてから解答に進んでみてください。
解答
$(1)\:15\quad(2)\:26\quad(3)\:3\sqrt2\quad(4)\:8$
解説
もちろん直角三角形なので三平方の定理の式を使って計算で求めることができます。
例えば$(1)$なら
$\begin{align}9^2+12^2=c^2\\81+144=c^2\\225=c^2\\c=\pm15\end{align}$
$\:c>0\:$なので$\:c=15$
といった具合で。
でも直角三角形であることを確認したうえで、短い辺と中間の長さの辺の比が$3:4$であることに気づければ、$3:4:5$の三角形と相似であることがわかります。
ということは
$5:4=c:12$の比例式を作れます。
($5:3=c:9$でもOK)

$(2)~(4)$も同様に、暗記しておくと良い三角形と関連させて解くことができます。
この方が楽ですね。
しかもこの方法に慣れてくると、計算せずとも数値を見た瞬間に解答できるようになります。
語呂合わせ
ところで世の中、語呂合わせにすると覚えやすいものがあります。
三平方の定理も何だかそのようで・・・。

例えば$3:4:5$の直角三角形。
語呂合わせにすると
「みよこ」だそうです。
女性の名前です。
ただこの語呂合わせで覚えるのは、男子にとってはかなりリスクがあると思います。
語呂合わせで覚える場合、たいてい小声で口に出して暗記するはずです。
「みよこ、みよこ、みよこ・・・」って。
で、それを聞かれる。
これがヤバい。
もしこれを読んでるキミが男子で、しかもキミに付き合ってる女子がいる、もしくは気になる女子がいるとする。
そこで「みよこ、みよこ、みよこ・・・」を小声で連発してたら、かなりの確率で浮気を疑われます。
それにそもそも名前を忘れてしまうと、思い出すためにいろいろな女性の名前を連呼することになります。
みちこ みつこ みさこ みなこ みやこ みくこ みとこ ・・・、
たらし確定です。本人にそんな気がなくても。

例えば$5:12:13$の直角三角形。
語呂合わせにすると
「こいつ父さん?」だそうです。
ところで世の男性陣にとって最も恐怖を感じるものの一つに、気になる女性の父親があります。
このサイトに何度か登場しているよしたか君は、よしえさんのことを好きの少し手前くらいで意識しています。
で、気になる女性が見知らぬ男と一緒にいるとどうしても気になるのが男の性(さが)であって・・・。
そこで聞くわけです。
「おいよしえ、誰だよこいつ、マジで!?」
「お父さんだけど。」

「こいつ父さん?(汗)」
気まずいです。かなり気まずい雰囲気になります。
よしたか君と父さんの距離が一番長いのがポイント。
よしえさんと父さんは親子なので距離が近いです。

三平方の定理を正三角形へ応用する問題
ここまで三平方の定理の基本を確認してきました。
最後にこのページのまとめとして、三平方の定理を正三角形に応用した問題を扱います。
ただ応用といってもごくごく初歩的な基本問題。
定期テストや高校入試で出題されたら正答必須の内容です。
基本例題3
1辺が$8cm$の正三角形がある。
$(1)\:$この正三角形の高さを求めよ。
$(2)\:$この正三角形の面積を求めよ。
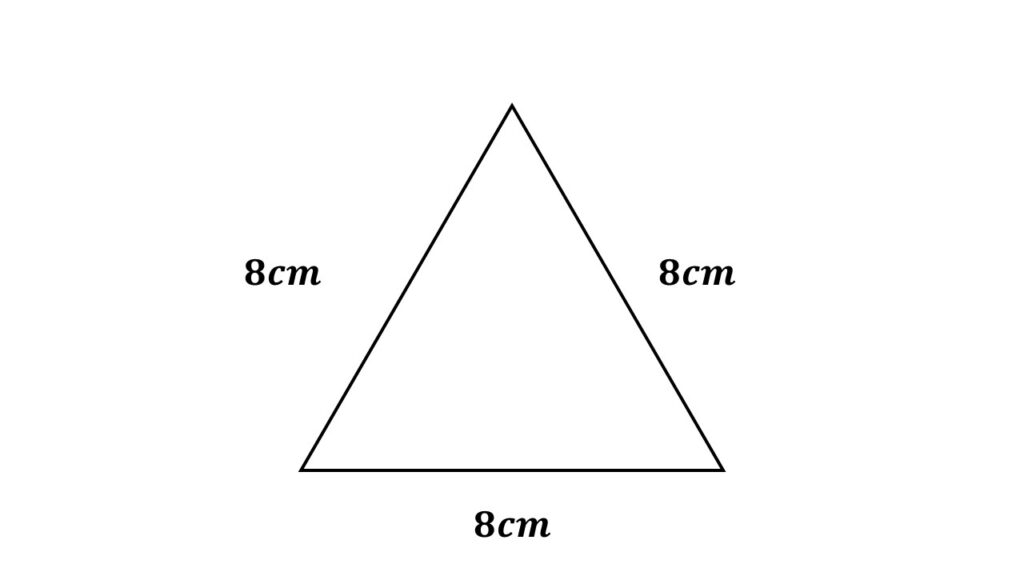
考え方
最終的に三角形の面積を求めるので、三角形の高さを求める必要があります。
正三角形の頂点から底辺に垂線を引いたものが高さです。
正三角形は二等辺三角形の性質がありました。
では、二等辺三角形の頂点から底辺に引いた垂線にはどんな性質があるか?
二等辺三角形の性質を忘れている人はこちらで復習しましょう。
垂線を引いたときにできる三角形に注目すると、特徴的な三角形が出てきます。
それをもとに高さを考えます。
高さが求まると三角形の面積の公式が使えます。
なお三平方の定理は正三角形には成り立ちません。
必ず直角三角形を見つける、もしくは強引に作り出してから三平方の定理を使います。
解答
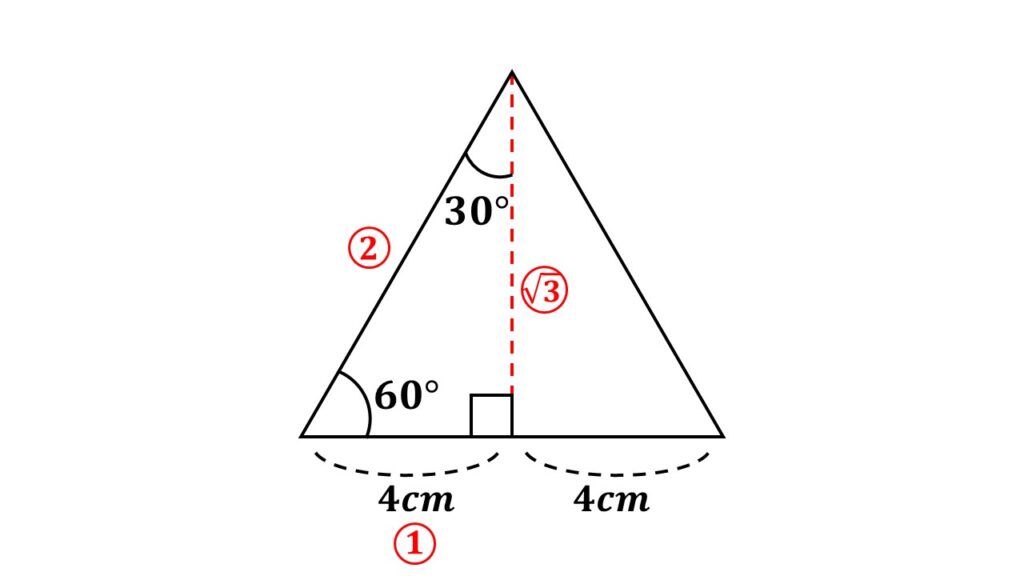
$(1)\:$正三角形の頂点から底辺に向け垂線を引くと垂線は底辺を二等分する
このときできる2つの三角形は、垂線によりできる$90°$と底角が$60°$から残りの角が$30°$の直角三角形となる
これより求める高さを$x$とすると
$\begin{align}1:\sqrt3&=4:x\\x&=4\sqrt3\end{align}$
よって高さは$4\sqrt3\:cm$
$(2)\:8\times4\sqrt3\times\dfrac{1}{2}=16\sqrt3\:cm^2$
解説
この基本例題3は問題と解き方をセットで覚えておきましょう。
$(1)$は$(2)$のヒントになっています。
というか、$(1)$がなくても自力で面積を求められるのが理想です。
三角形の高さを求めるために三平方の定理を使います。
高さを求める際、上記解答では暗記しておいたほうが良い三角形の性質$1:\sqrt3:2$を使いました。
もちろん三平方の定理を使って地道に計算して高さを求めることも可能です。
$\begin{align}4^2+x^2&=8^2\\x^2&=64-16\\x^2&=48\\x&=\pm4\sqrt3\end{align}$
ただどちらが楽かといったら、$1:\sqrt3:2$を使った方ですよね。
このように、暗記しておいた方が良い三角形は何かと計算の手間を省いてくれます。
「三平方の定理で計算すると辺の比の性質が求められる」ということを踏まえたうえで、暗記しておいた方が良い三角形をうまく使っていきましょう。

