ここでは指数の計算について、特に間違えやすいところを解説します。
間違えやすいからこそ、テストでも出題されやすい部分。指数の性質をしっかり理解しておきましょう。
累乗 指数 とは？
累乗とは同じ数をいくつかかけ算したもののことをいいます。
例えば、2を4回かけ算したとします。すると式は
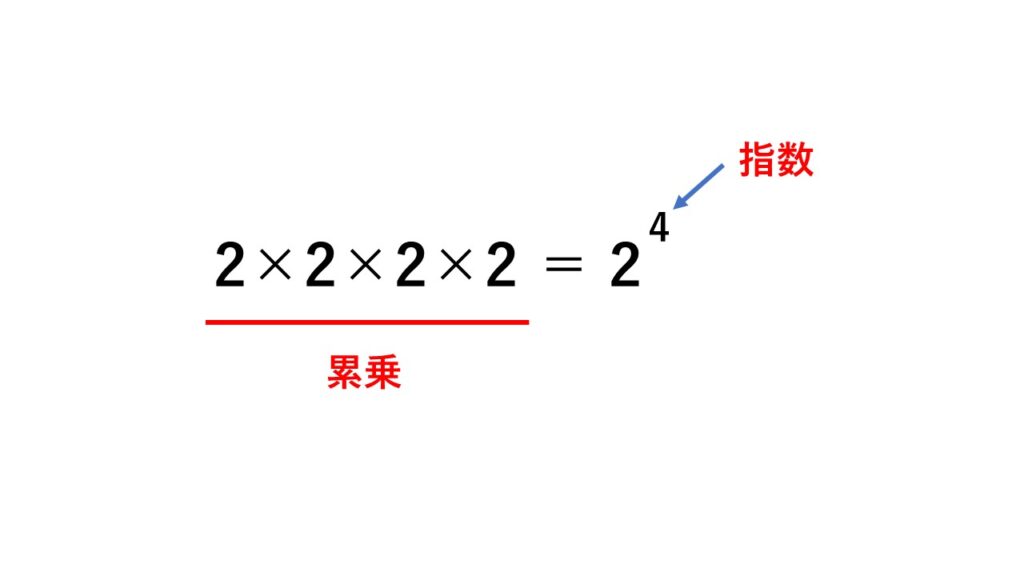
$2\times2\times2\times2$
となりますよね。これが累乗です。
そしてこれはもっとコンパクトに
$2^4$ と書けます。
この右上についた小さい数字のことを指数（しすう）といい、『2の4乗（2の4じょう）』と読みます。
かける回数が多い時には、指数を使って表した方が見やすく考えやすくなります。
ということは、
$2\times2\times2$ は $2^3$
$2\times2$ は $2^2$ となります。
そして
$2$ は $2^1$ となります。ただ指数が1ならふつうは書きません。
ちなみにですが、$2^0$ は $1$ です。
どんな数でも0乗は$1$と定義されています。
負の数と指数
上の例では何ら難しいことは無いのですぐ理解できると思います。
でも負の数が関わってくると、中学1年生のほぼ100％が1回は間違える部分があります。
それが以下にあげるものです。
●$(-3)^2$ と $-3^2$ の違い●
この違い、わかりますか？
$(-3)^2$ は $-3$ を2回かけ算することを表します。つまり
$(-3)^2=(-3)\times(-3)$ で $9$ となります。
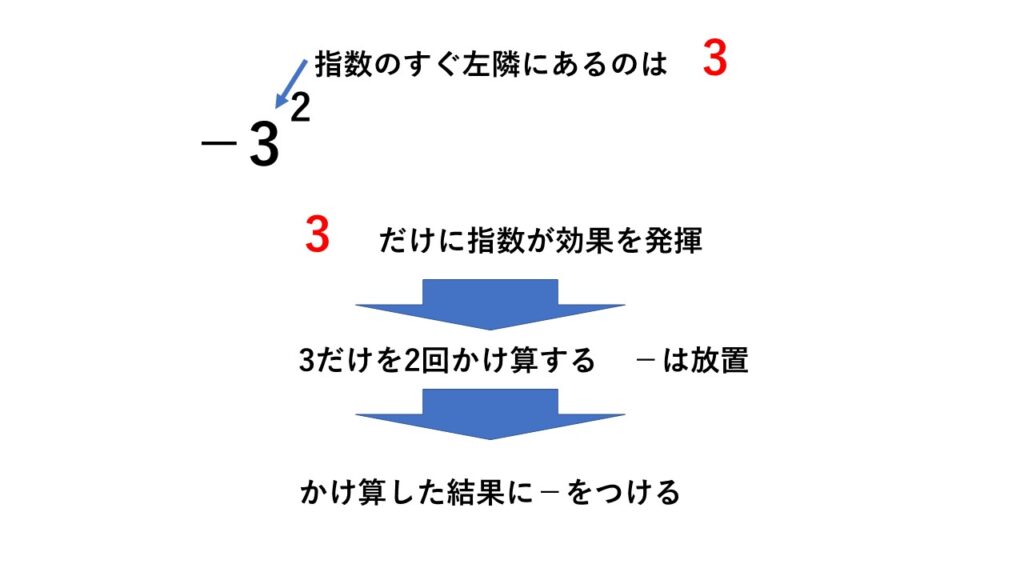
一方 $-3^2$ は $3$ を2回かけ算することを表し
$-3^2=-(3\times3)$ で $-9$ となります。
この2つの違い、そういうこととして覚えるしかないのですが、
「指数はそのすぐ左隣にあるものについて効果を発揮する」
と考えると良いでしょう。
●$-3^2$ をもう少し詳しく●
$-3^2$ は $-(+3)^2$ ということです。
さらに厳密に書くと$-1\times(+3)^2$ です。
正の数を表す$+$は省略して書くことができました。その省略したものが$-3^2$ です。
指数はそのすぐ左隣にあるものに効果を発揮するから、 ） に効果を発揮します。
つまり $(+3)$ に効果を発揮する。
結果として$(+3)\times(+3)=9$ となり、それに$-1$をかけ算して$-9$となるわけです。
指数はそのすぐ左隣にあるものについて効果を発揮する
テストによく出る指数の計算
以下に指数計算の具体例としていくつか挙げておきます。どれも間違えやすい計算だったり、迷いやすい問題です。
$2\times3^2=2\times9=18$
←指数がある部分を最優先で計算。
$3^2=3\times3=9$
$2^3\times3^2=8\times9=72$
←指数がある部分を最優先で計算。
$2\times(-3)^2=2\times9=18$
←指数の2はすぐ左隣にあるもの、この場合 ）に効果を発揮。$(-3)\times(-3)=9$
$2\times(-3^2)=2\times(-9)=-18$
←指数の2はすぐ左隣にあるものに効果を発揮。この場合3のみに働く。
$10-(-3)^2=10-9=1$
←指数が効果を発揮するのは$(-3)$に対してのみ。その左にある$-$はいったん放置しておく。
$10+(-3)^2=10+9=19$
←指数が効果を発揮するのは$(-3)$に対してのみ。その左にある$+$はいったん放置しておく。
$2^3\times(-2)^3=8\times(-8)=-64$
←$2$と$-2$は別々の数値なので別々に計算する。
$(-2)^3=(-2)\times(-2)\times(-2)=-8$
$(\dfrac{2}{3})^2$$=\dfrac{2}{3}\times\dfrac{2}{3}=\dfrac{2\times2}{3\times3}=\dfrac{4}{9}$
←指数の2はすぐ左隣にあるもの ） に効果を発揮する。（かっこ）の中がひとまとまり。
$+(\dfrac{2^2}{3})=\dfrac{4}{3}$
←この場合、指数は分子の2だけに効果を発揮する。
$-(\dfrac{2^2}{3})=-\dfrac{4}{3}$
←この場合、指数は分子の2だけに効果を発揮する。指数を最優先で計算する。$-$はいったん放置しておく。
指数計算の規則性
ここから先は上記の内容をしっかり理解してから読み進めてください。
次に少しレベルを上げて指数計算の特徴を見ていきます。
絶対に覚えないといけないといった内容ではありませんが、知っておくと複雑な計算をするときに役立ちます。
基本例題1
次の計算結果を、累乗の指数を使って表せ。
$\begin{align}(1)&\:\;2^3\times2^2\quad&(2)&\:\;3^2\times3^1\\(3)&\:\;5^2\times5\quad&(4)&\:\;2^2\times2\times2^3\end{align}$
考え方
通常、特に指示がない限り累乗の指数で表す必要はありませんが、この問題については累乗の指数で答えてください。
問題と計算結果に気付いてほしい点があります。
一通り答えを自力で出してから解答に進みましょう。
解答
$\begin{align}(1)\:\;&2^3\times2^2=2\times2\times2\times2\times2\\=&\;2^5\end{align}$
$\begin{align}(2)\:\;&3^2\times3^1=3\times3\times3\\=&\;3^3\end{align}$
$\begin{align}(3)\:\;&5^2\times5=5\times5\times5\\=&\;5^3\end{align}$
$\begin{align}(4)\:\;&2^2\times2\times2^3=2\times2\times2\times2\times2\times2\\=&\;2^6\end{align}$
指数と解答にある法則は？
改めて問題と解答を並べます。指数に注目してください。
$\begin{align}2^3&\times2^2&＝&\;2^5&\\3^2&\times3^1&=&\:3^3&\\5^2&\times5&=&\:5^3&\end{align}$
$2^2\times2\times2^3=2^6$
例えば
$2^3\times2^2$では$3$乗と$2$乗があります。
その解答は$2^5$で$5$乗があります。
指数に注目すると$3$と$2$をたして$5$となっています。
他の問題も同様に指数に注目すると、それぞれ足したものが解答の指数と一致しています。
このように指数があるかけ算では、指数を足したものがその計算結果の指数となります。
$X^a\times X^b=X^{(a+b)}$
ただし底が同じときに限ります。そのため例えば、
$2^3\times3^2$のように底が異なるときは地道に計算するしかありません。
この関係はわり算のときにも成り立ちます。
ただしかけ算のときには指数を足したのに対し、わり算では指数を引きます。
$2^3\div 2^2=2$
これだけでは全く説明になってないのでもう少し詳しく見てみましょう。
なぜわり算のときは指数を引くのか？
わり算は分数で表すことができました。すると
$2^3\div 2^2=\dfrac{2^3}{2^2}\quad$となります。これを一度指数がない形に置き換えます。
$\dfrac{2\times2\times2}{2\times2}\quad$これ、約分できますね。すると$2$です。
$2^3\div 2^2=2^1$を指数について注目すると、$3-2$の結果が答えの指数$1$と一致しています。
別の例も見て確認しましょう。
$3^2\div 3^1=\dfrac{3\times3}{3}=3^1$
$2^5\div 2^3=\dfrac{2\times2\times2\times2\times2}{2\times2\times2}=2^2$
確かに指数部分に注目すると引き算した形になっています。
$X^a\div X^b=X^{(a-b)}$
ただし$\;a>b$
$a>b$とは$a$の方が$b$よりも大きい数ということです。
なお$b>a$の場合、$X$の指数部分が負の数となるため中学では扱いません。
例えば
$2^3\div2^4$
のように、割る数にある指数の方が割られる数にある指数よりも大きいものは中学では扱いません。
わり算の場合も底が同じときに限ります。そのため例えば、
$2^3\div3^2$のように底が異なるときは地道に計算するしかありません。