このページではおうぎ形の導入から始め、定期テストなどでよく出題される基本問題の解き方までを解説します。
おうぎ形とはどんな図形か
おうぎ形とは
円の2つの半径と弧で囲まれた図形
のことをいいます。
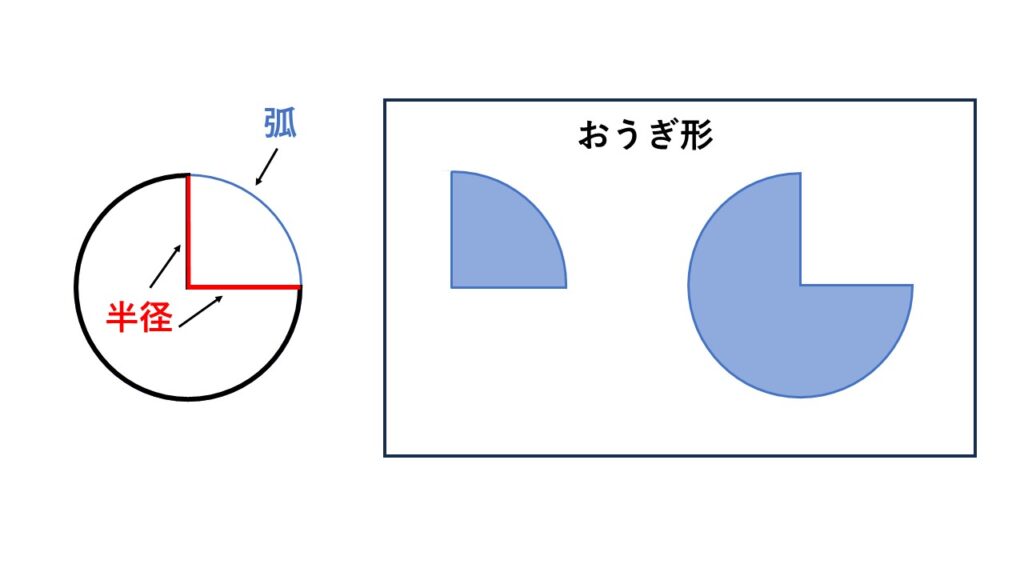
2つの半径で円を切り取ると、おうぎ形が2つできます。
おうぎ形は円の一部分と考えましょう。
おうぎ形は円の一部分。すると当然中心があります。
その中心をアルファベットOを使って、点Oと表します。
円周上に点A、Bがあるとき、点Oから点A、Bをそれぞれ結んだ線分が、おうぎ形の半径となります。
また、点Aから点Bへ円周上に沿った部分（図の青い線）のことを弧といいます。
弧$AB$や$\stackrel{\Large\frown}{AB}$と表します。
円周上の点A、Bを結ぶ線分のことを弦といい、
弦$AB$と表します。
ただ、弦$AB$は結局線分ABのことなので、
単にABと表しても間違いではありません。
おうぎ形の面積と弧の長さ 公式
おうぎ形の面積＝半径×半径×$3.14$×$\dfrac{中心角}{360}$
おうぎ形の弧の長さ＝直径×$3.14$×$\dfrac{中心角}{360}$
おうぎ形の面積や弧の長さは、中心角の大きさに比例する
おうぎ形は円の一部と書きましたが、中心角が$360$°に満たないものがおうぎ形といえます。
ということは、
おうぎ形は中心角に注目して考える
ことになります。
円の面積＝半径×半径×$3.14$ と学びました。
そして半円の面積を求める時は、円の面積を$\dfrac{1}{2}$倍して求めたはずです。（半円はおうぎ形です）
この$\dfrac{1}{2}$倍が中心角のことを表しています。
つまり円の中心角を$\dfrac{180}{360}$と考え、結果$\dfrac{1}{2}$となり円の面積を$\dfrac{1}{2}$倍するという流れ。
おうぎ形の弧の長さについても同様です。
円周の長さ＝直径×$3.14$ と学びました。
中心角の大きさにより円周（弧の長さ）が変わってくるので、
おうぎ形の弧の長さ＝直径×$3.14$×$\dfrac{中心角}{360}$ となります。
おうぎ形の面積、弧の長さを求める練習
ここまでのことを踏まえ、おうぎ形の面積や弧の長さを求める練習をします。
おうぎ形の問題自体は決して難しくないので、テストでは必ず解けるようにしましょう。
これ以降、円周率3.14は$π$としていきます。
基本例題
半径$6$㎝、中心角が$120$°のおうぎ形の面積と弧の長さを求めよ。
考え方
おうぎ形の面積＝半径×半径×$\pi$×$\dfrac{中心角}{360}$
おうぎ形の弧の長さ＝直径×$\pi$×$\dfrac{中心角}{360}$ の式をそのまま使います。
直径は$2\times$（半径）です。
解答
面積＝$6\times6\times\pi\times\dfrac{120}{360}$
$=36\pi\times\dfrac{1}{3}$
$=12\pi$（$cm^2$）
弧の長さ＝$2\times6\times\pi\times\dfrac{120}{360}$
$=12\pi\times\dfrac{1}{3}$
$=4\pi$（$cm$）
式をそのまま使うだけだから難しいことはありませんね。
類題で練習して解き方を覚えてしまいましょう。
類題1
(1)半径$8$㎝、中心角$45$°のおうぎ形の面積と弧の長さを求めよ。
(2)半径$6$㎝、中心角$60$°のおうぎ形の面積と弧の長さを求めよ。
(3)半径$6$㎝、中心角$150$°のおうぎ形の面積と弧の長さを求めよ。
(4)半径$9$㎝、中心角$160$°のおうぎ形の面積と弧の長さを求めよ。
(5)半径$6$㎝、中心角$270$°のおうぎ形の面積と弧の長さを求めよ。
解答はこのページの最後にあります。
次におうぎ形の中心角を求める練習をします。
といっても解き方自体は特に変わりません。
おうぎ形の中心角を求める
おうぎ形の中心角を求める問題もテストではよく出題されます。
この問題もしっかり解けるようにしておきましょう。
基本例題
(1)半径$8$㎝、弧の長さ$4\pi$㎝のおうぎ形の中心角を求めよ。
(2)半径$3$㎝、面積$3\pi$$㎝^2$のおうぎ形の中心角を求めよ。
考え方
おうぎ形の面積＝半径×半径×$\pi$×$\dfrac{中心角}{360}$
おうぎ形の弧の長さ＝直径×$\pi$×$\dfrac{中心角}{360}$
の式にあてはめ、求める中心角を$x$として計算を進めます。
解答
求める中心角を$x$とする
(1) おうぎ形の弧の長さ＝直径×$\pi$×$\dfrac{中心角}{360}$ より
$4\pi=2\times8\times\pi\times\dfrac{x}{360}$
$4\pi=\dfrac{16}{360}\pi$$x$
両辺$\pi$で割って
$4=\dfrac{16}{360}x$
両辺360倍して
$1440=16x$
$x=90$
よって求める中心角は$90$°
(2) おうぎ形の面積＝半径×半径×$\pi$×$\dfrac{中心角}{360}$ より
$3\pi=3\times3\times\pi\times\dfrac{x}{360}$
$3\pi=\dfrac{9}{360}\pi$$x$
$1080=9x$
$x=120$
よって求める中心角は$120$°
おうぎ形は円の一部ということを踏まえれば、特に難しいことはありません。
面積を求める式や弧の長さを求める式も、暗記するのではなく円の一部と考えれば、すぐにわかると思います。
それでは類題で解き方を覚えてしまいましょう。
類題2
(1)半径$9$㎝、弧の長さ$2\pi$㎝のおうぎ形の中心角を求めよ。
(2)半径$4$㎝、弧の長さ$3\pi$㎝のおうぎ形の中心角を求めよ。
(3)半径$10$㎝、面積$20\pi$㎝$^2$のおうぎ形の中心角を求めよ。
(4)半径$5$㎝、面積$10\pi$㎝$^2$のおうぎ形の中心角を求めよ。
弧の長さが与えられているのか、面積が与えられているのかには注意しましょう。
おうぎ形の面積を求める式 練習問題
ここまでのまとめとして、次の問題を使って実力をつけていきましょう。
【練習問題】
$1$辺$10$㎝正方形の中にある斜線部分の面積を求めよ。
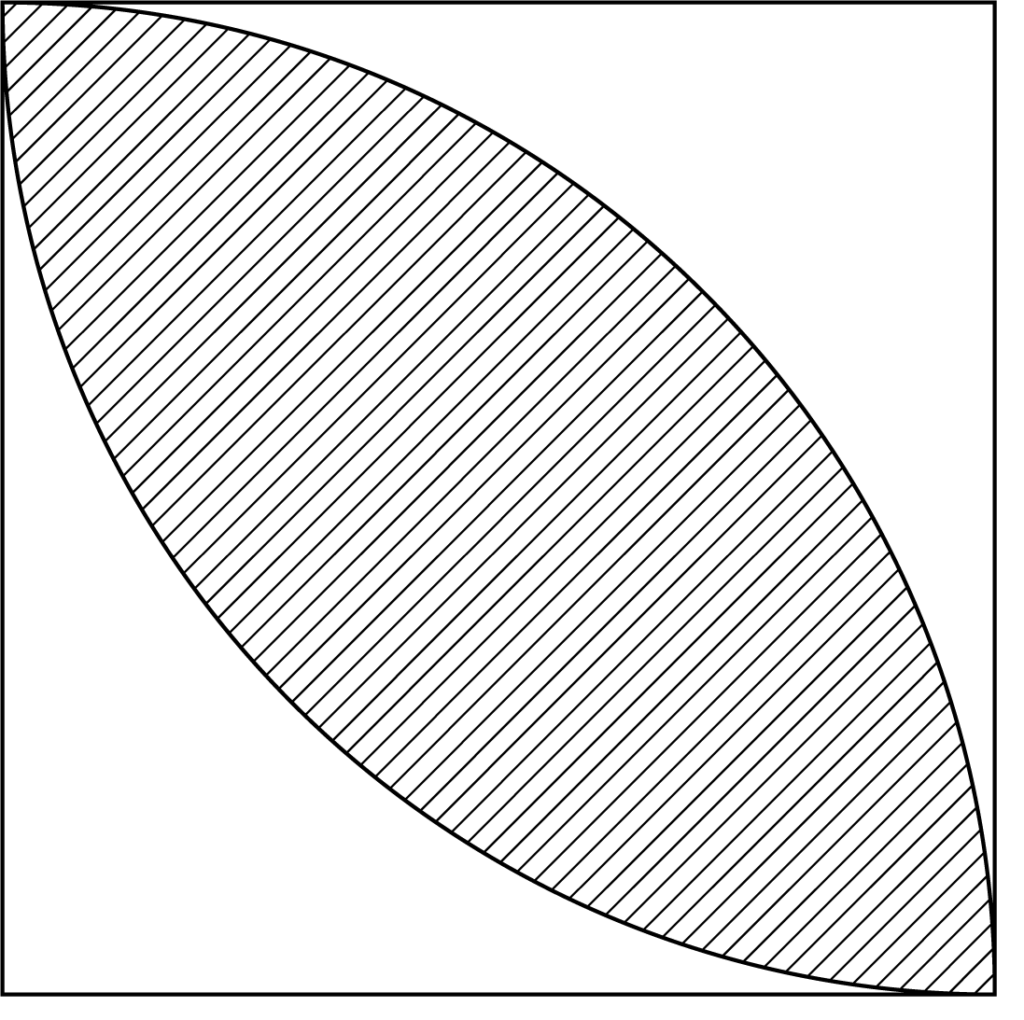
教科書にも掲載されるような、おうぎ形の面積を求める式を使う代表的な問題です。
まずはしっかり考えてください。
直接斜線部分の面積を求めようとしても式を作れないので、少し視点の切り替えが必要になります。
解答は動画で。
1つの図の中にたくさんの線が含まれると、なかなか特定の図形（この問題の場合はおうぎ形）に気づけないものです。
ただここで挙げた練習問題は基本中の基本なので、問題と解き方をそのまま覚えてしまっても良いでしょう。理解できたら動画で紹介した方法の他に別の解き方はないか考えてみてください。
この問題の解き方を踏まえた上で、もう少し複雑な面積を求める問題も入試などでは出題されます。
類題解答 式をそのままあてはめるだけなので結果だけ掲載します。
類題1
(1)面積$8\pi$（$cm^2$） 弧の長さ$2\pi$（$cm$）
(2)面積$6\pi$（$cm^2$） 弧の長さ$2\pi$（$cm$）
(3)面積$15\pi$（$cm^2$） 弧の長さ$5\pi$（$cm$）
(4)面積$36\pi$（$cm^2$） 弧の長さ$8\pi$（$cm$）
(5)面積$27\pi$（$cm^2$） 弧の長さ$9\pi$（$cm$）
類題2
(1)$40$° (2)$135$° (3)$72$° (4)$144$°