濃度の考え方の超基本

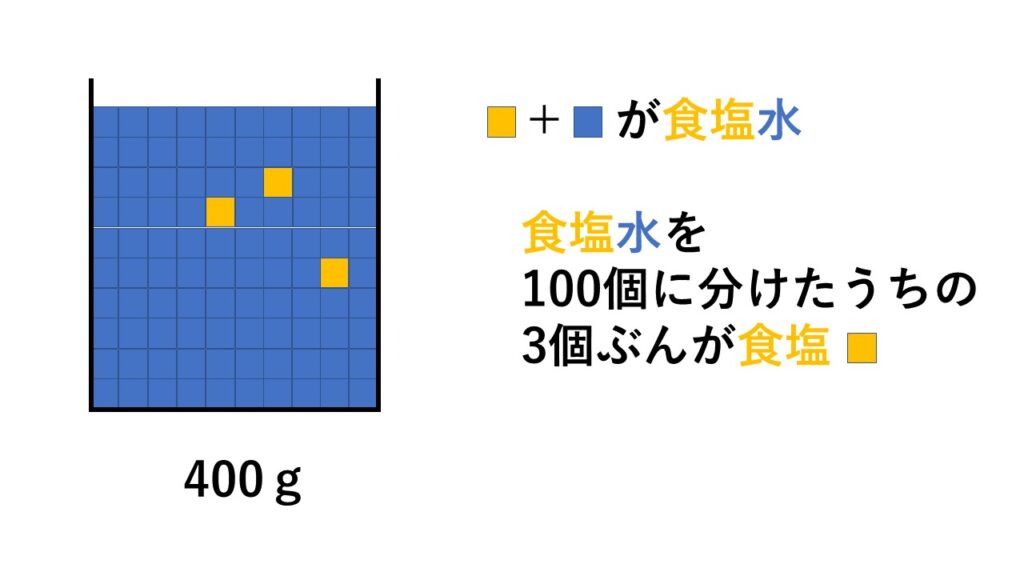
濃度の問題を考えるための大前提

濃度とはざっくり言うと、「どれくらい溶けているか」ということです。 だから「食塩水の濃度」といったら、「その水にはどれくらい食塩が溶けているか」ということになります。

ところで「100個に分けたうちの3個ぶん」とは
100分の3のことで、
100分の3は0.03のことで、
0.03は3％でした。
つまり見かけはちがうけど、

$\dfrac{3}{100}$と$0.03$と$3$%は同じ意味で

「100個に分けたうちの3個ぶん」です。

すると「400を100個に分けたうちの3個ぶんはいくつですか？」
といわれたら
$400\times\dfrac{3}{100}$
の計算をすることになります。

「分ける」からまず「わり算」。
$400\div100$
次にそれが「3個ぶん」あるから「かけ算」をする。
$400\div100\times3$
わり算は分数に直してかけ算にできるから、
$400\times\dfrac{1}{100}\times3$　となり　$400\times\dfrac{3}{100}$
よって、12と求まります。

濃度の考え方はこれがもとになっています。
この大前提をふまえ、食塩水の濃度(％)を考えます。

食塩水の濃度と食塩の量

いいですか？　ここでとても大事なことを書きます。

食塩水とは食塩と水を混ぜた液体のことです

そんなの当たり前だ、分かりきってる。ふざけるなっ!!　と思った人ほど要注意。
濃度の問題では応用問題になればなるほど、この極めて当たり前のことが出てこなくなります。

超基本例題1　400ｇの食塩水に12ｇの食塩が入っている時、この食塩水の濃度は何％ですか。

考え方　食塩水の濃度を求める計算は、
（食塩の量）$\div$（食塩水の量）$\times100$

解答　$12\div400\times100$

$=\dfrac{12}{400}\times100=\dfrac{3}{100}\times100$

$=3$

よって　$3$%

●濃度3％の食塩水の意味●

上記の問題では濃度3％と出ました。3％とは「100個に分けたうちの3個ぶん」でしたね。
ということは、
「食塩水400ｇを100個に分けたうちの3個ぶん食塩が溶けている」
という意味になります。

$400\times\dfrac{3}{100}=12$　で確かに問題文の通り、12ｇの食塩が溶けていると数値で出てきました。
ということは、「400ｇのうち388ｇが水」ということもわかります。
当たり前のことを繰り返しますが、食塩と水を混ぜた液体が食塩水ですからね。
12ｇ+388ｇで400ｇですからね。

超基本例題2　水100ｇに食塩が3ｇ溶けています。この食塩水の濃度は何％ですか。

考え方　はぁ？　100ｇに3g、簡単じゃねぇか、3%だろ!!　と思ったそこの君、大間違いです。
このように考えた人は、上記のとても大事なことを鼻で笑った人かもしれません。
100ｇは水の量。当然食塩水は100ｇよりも重くなります。
食塩水の濃度＝（食塩の量）$\div$（食塩水の量）$\times100$

解答　$3\div(100+3)\times100=3\div103\times100$
$=300\div103$
$=2.912621$

103が何なのかわからない人は、とても大事なことをよ～く読んでください。

●食塩水の濃度から食塩の量を求める●

食塩水の濃度＝（食塩の量）$\div$（食塩水の量）$\times100$
この関係式を使うと、濃度から食塩の量を求めることができます。

超基本例題3　濃度7％の食塩水200ｇの中に含まれる食塩の量は何ｇですか。

考え方　上記関係式をそのまま当てはめます。

解答　$7=(食塩の量)\div200\times100$

$7=\dfrac{食塩の量}{200}\times100$

$7\times200=(食塩の量)\times100$

$0.07\times200=14$　より
食塩の量は14ｇある。

補足　食塩水の量と濃度がわかっていると、そこに含まれる食塩の量を求めることができます。
そのために上記の関係式を使っていきます。
そこで解答の

$0.07\times200=食塩の量$　に注目。

これは結局のところ、
濃度に食塩水の量をかければ食塩の量が求まる
ということ。

等式の性質を考えればなんてことないのですが、このことを覚えておくだけでも濃度の問題を解くのがだいぶラクになってきます。

（食塩の量）＝（濃度）×（食塩水の量）　で求まる