二等辺三角形の性質

二等辺三角形の定義と定理

定義とは、決めごと・約束事の意味でした。よって

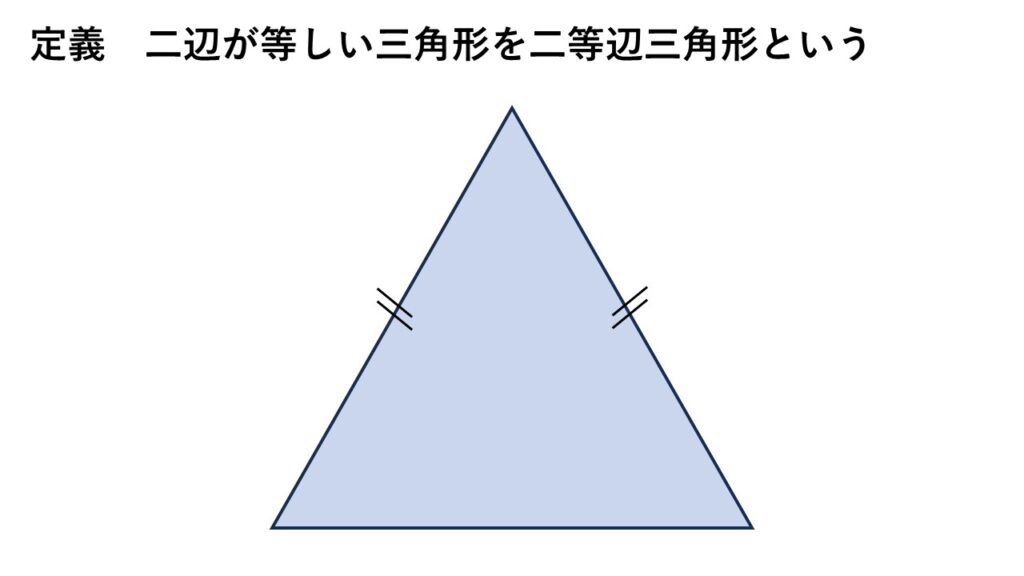
二等辺三角形の定義
二辺の長さが等しい三角形

となります。

もう少し日常的な言葉使いに翻訳すると、
「二辺の長さが等しい三角形のことを二等辺三角形ということに決めましょう」
となります。

定理とは性質のことで、その正しさが証明されているものでした。
二等辺三角形には覚えておくべき重要な定理があります。

この2つの定理はしっかり覚えておきましょう。

ところで定理は、その性質の正しさが証明されているものと書きました。
ということで、この2つの定理についてその正しさを証明していきます。
定理もそうですが、その証明もしっかりおさえておきましょう。
自力で証明できるようにしてください。

二等辺三角形の底角は等しいことの証明

基本例題


図のような$AB=AC$である二等辺三角形の底角$∠ABC$と$∠ACB$は等しくなることを証明せよ。

考え方
仮定：$AB=AC$　　結論：$∠ABC=∠ACB$
基本例題の図だけで考えても先に進まないので少し工夫をします。
「角の大きさが等しい」ということは「重ねた時にピッタリ重なる」ということですね。
で、「ピッタリ重なる」ということは「合同」ということ。

つまり$△ABC$を$∠ABC$と$∠ACB$が重なるように折り曲げると、折り目を境に2つの三角形ができる。
この「2つの三角形が合同だ」ということを証明すれば、対応する角も等しくなる。
ということで結果的に底角が等しいということを証明したことになります。

これをふまえ証明を進めます。
なお図形の端と端が重なるように折り曲げるということは、折り目はちょうど真ん中にきます。

証明

底辺$BC$の中点を$M$とし、頂点$A$と$M$を結ぶ
$△ABM$と$△ACM$において
仮定より
$\begin{align}AB&=AC&①\\BM&=CM&②\end{align}$
$AM$は共通なので$AM=AM$　③

①②③より3組の辺がそれぞれ等しいので
$△ABM≡△ACM$
対応する角は等しいので
$∠ABM＝∠ACM$
よって二等辺三角形の底角は等しいといえる
証明終わり

二等辺三角形の頂角の二等分線は底辺を垂直に二等分することの証明

基本例題


図のような$AB=AC$である二等辺三角形で、頂角の二等分線は底辺を垂直に二等分することを証明せよ。

考え方
仮定：$AB=AC$　　結論：$∠AMB=∠AMC=90°$　$BM=CM$
ここでも三角形の合同を証明していきます。
ただここで悩ましいのが
$∠AMB=∠AMC=90°$
であることをどうやって表すか？
単に$∠AMB=∠AMC$を示すだけなら三角形の合同を証明するだけで良いのですが、具体的に角度が$90$°であることを示すにはもう少し手の込んだ証明が必要になります。

そこで注目するのが直線の角度について。
直線は角度でいうと$180$°です。このことを使って$∠AMB=∠AMC=90°$を示します。

なお、$BM=CM$は結論であるため、三角形の合同を証明する際にこれは使えません。
よって「点$M$は$BC$の中点なのかどうかわかっていない」という体で証明しなければなりません。

証明

$△ABM$と$△ACM$において
仮定より
$\begin{align}AB&=AC&①\\∠BAM&=∠CAM&②\end{align}$
$AM$は共通なので$AM=AM$　③

①②③より2組の辺とその間の角がそれぞれ等しいので
$△ABM≡△ACM$

長い証明でしたね。まぁもう少しコンパクトに証明することもできますが、ここは説明も兼ねていたので1つ1つかみ砕いた形で証明を進めました。
定義や定理、証明を暗記するのではなく、筋道立てて考えて、理解するようにしましょう。

$90°$であることの示し方
直線は$180°$であることを使い、大きさの等しい2つの角を合わせたものが$180°$となっていることを示す。

逆　反例

• 逆　　仮定と結論を入れかえたもの
• 反例　あることがらが成り立たないことの例

唐突に「逆」「反例」と書きましたが、理屈で物事を考える時に「逆」を考えることはとても大切です。
例として「3つの辺が全て同じ長さの三角形ならば、正三角形である。」を考えます。
仮定は「3つの辺が全て同じ長さの三角形」
結論は「正三角形である」　です。

この仮定と結論を入れかえた「逆」は
「正三角形ならば、3つの辺が全て同じ長さ（の三角形）である。」
です。
そして逆を考えたら必ず、正しいか正しくないかを考えます。
で、この逆は正しいです。

別の例として「$1+1$ならば$2$である」を考えます。
仮定は「$1+1$」
結論は「$2$である」　です。
この仮定と結論を入れかえた「逆」は
「$2$ならば、$1+1$である。」です。

さて、これは正しいでしょうか？

一見正しい様に感じます。確かに$2=1+1$になりますから。
ただ$2$となるのは$1+1$のときだけではありませんよね？
$3-1$や$2\times1$など、無限に考えられます。
よって「$2$ならば、$1+1$である。」は正しくない、といえます。
このように「逆」は必ずしも正しいとは言い切れません。
この正しくないものの具体例が反例です。（上記では$3-1$や$2\times1$）

これは数学の証明のときに限ったことでなく、日常生活の中でもそういえます。

「テスト前ならば勉強している」

仮定：テスト前
結論：勉強する

逆：勉強しているならばテスト前だ

逆は正しいでしょうか？　というと、正しくないですよね？
テスト前でも勉強しない人は勉強しないです。
それにテスト前じゃないのにこのサイトを観ているということは、テスト前じゃないのに勉強していることになります。

「イケメンならばモテる男である」

仮定：イケメン
結論：モテる男である

逆：モテる男ならばイケメンである

逆は正しいでしょうか？

二等辺三角形になるための条件

「逆」について学んだところで再び二等辺三角形に話を戻します。

この二等辺三角形になるための条件も重要なので覚えておきましょう。
これは二等辺三角形の定理の逆を考えています。
二等辺三角形の定理の逆は正しいといえます。ではどうして正しいといえるのか？

2つの辺が等しいと二等辺三角形となる理由

もっともこれは二等辺三角形の定義なので証明するまでもありません。

2つの角が等しいと二等辺三角形となる理由

このことは三角形の合同を使って次のように説明できます。

$△ABC$で$∠B=∠C$ならば$AB=AC$の二等辺三角形となっていることを証明します。

仮定：$∠B=∠C$
結論：$AB=AC$

（この時点では$BM$と$CM$等しいかどうかはわかりません）

頂角の二等分線が底辺を垂直に二等分すると二等辺三角形になる理由

これも三角形の合同を証明すると説明できます。

頂角の二等分線が底辺を垂直に二等分する様子を図に表します。
これは図を見た瞬間に証明できてほしい内容です。

仮定：$∠BAM=∠CAM$　$∠AMB=∠AMC$
結論：$AB=AC$

数学では図形を単に図形として見るのではなく、図形を理論立てて見る姿勢が求められます。
ここまで証明ばかりでしたが、理論的に考えるための基本が詰まっています。
何度も繰り返し学習するようにしてください。

正三角形の定義と定理

二等辺三角形と合わせて、正三角形についても覚えておきましょう。

正三角形の定義
3つの辺の長さが等しい三角形

正三角形の定理
3つの角の大きさは等しい（それぞれ60°となっている）

もっとも、3つの角のうちの2つが60°なら（この時点で二等辺三角形となるのは確実）、残りの角も60°になりますよね。

正三角形は二等辺三角形の特別な状態のものと考えてください。
そのため正三角形は二等辺三角形の性質がそのまま当てはまります。