
相似な図形の面積比は相似比の2乗に等しくなる
相似の考え方を発展させると、図形を考える際の様々な計算を楽にできるようになります。
もっとも相似比をしっかり理解しているという前提はありますが・・・。
このページではなぜ相似比の2乗は面積比と等しいのかについてじっくり解説します。
正方形の面積比と相似比の関係
冒頭にも書いた通り、
相似な図形の面積比は相似比の2乗に等しくなります。
これはどんな図形にもいえます。
具体例として最も考えやすい正方形で見てみましょう。
1辺が$1cm,2cm,3cm,4cm$の正方形があります。
相似比は$1:2:3:4$ですね。
そして面積はそれぞれ$1cm^2,4cm^2,9cm^2,16cm^2$なので
面積比は$1:4:9:16$です。
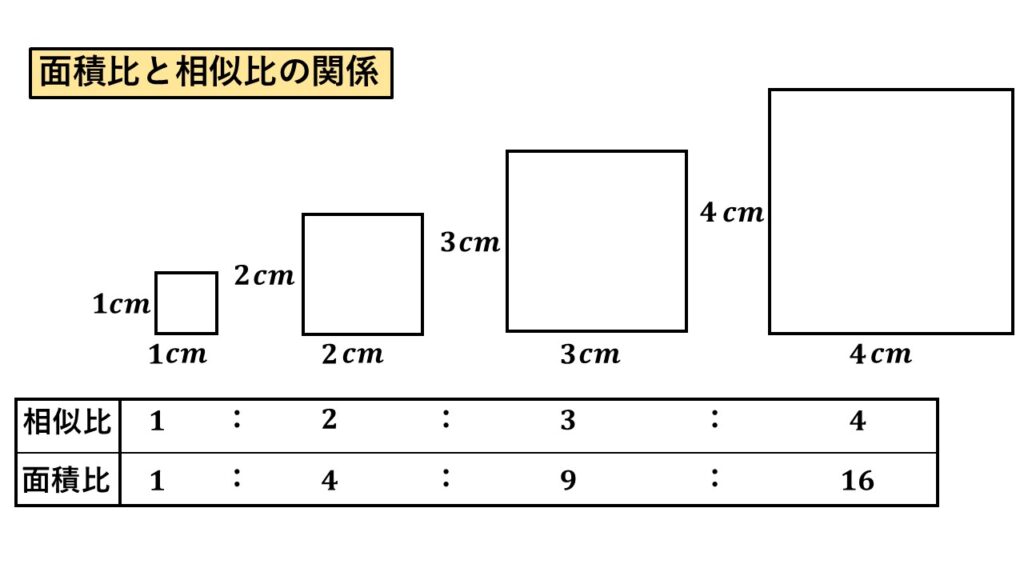
確かに面積比は相似比の2乗になってます。
でもこの書き方では$1cm,2cm,3cm,4cm$のときだけを説明しているに過ぎません。
他の大きさの正方形でも成り立つ、つまりどんな正方形についても一般的に成り立つことを説明するには、文字を使って説明する必要があります。
ということでもう少し本格的に見ていきます。
なお、以下の内容は色々と文字が出てきて説明自体も長く、レベルも少しUPしています。
基本の理解を優先したい人は下記の「相似比と面積比の基本例題」まで飛んでください。
なぜ面積比は相似比の2乗に等しくなるのか
説明するための前提知識
例えば1辺の長さを文字$k$で表すとします。(文字の種類は何でも良い)
そこに相似比$1:2$の正方形があった場合、
$1k:2k\quad$
として表すと、$1:2$の関係の正方形全てを表したことになります。
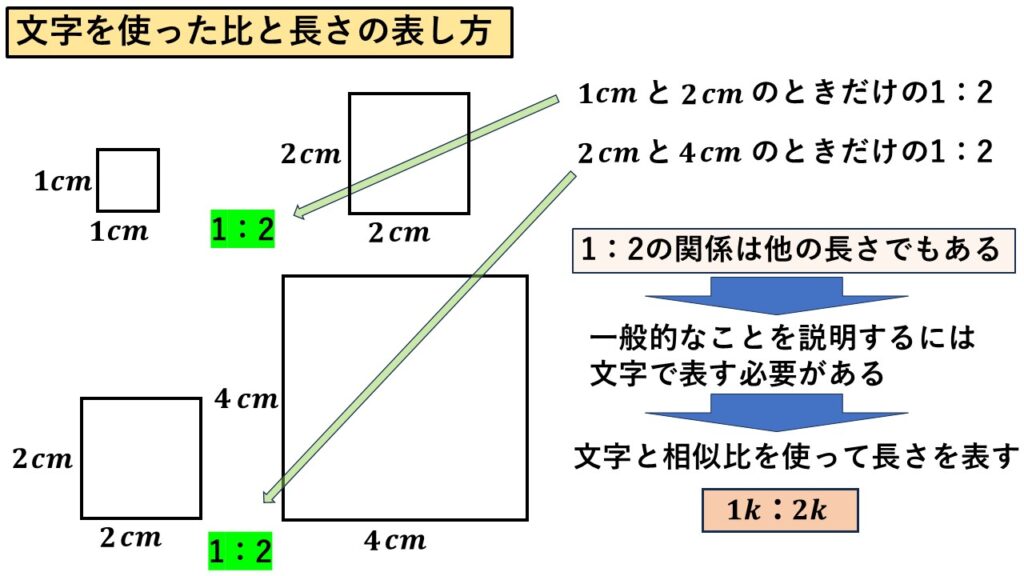
もちろん$k$には適当な数値を当てはめて良いので、
$k=1$なら1辺$1cm$と$2cm$の正方形を表しているし、
$k=2$なら1辺$2cm$と$4cm$の正方形を表していることになります。
もし相似比$3:5$の正方形全てを表したいなら
$3k:5k$ とします。
比は、長さを基に数値として表してますよね。
でも比は、長さを表しているわけではありません。
そのため図形の長さを比と絡めて説明するときは、比の状態のままではなく、長さを表した状態にしないと説明が進まなくなります。
そのため$1k:2k$のように長さ$k$と比を使って表すようにします。
そしてこの表し方は正方形に限らず、どんな図形にも当てはまります。
長くなりましたがここまでが前提知識。
このことを踏まえて面積比は相似比の2乗に等しくなることの説明に戻ります。
面積比は相似比の2乗に等しいことの説明
比も$1:2$としてしまうと$1:2$のときだけの説明になってしまいます。
そのため比も文字を使って$m:n$とします。
これでどんな比の関係でも説明したことになります。
相似比を$m:n$とすると
相似な2つの正方形の1辺はそれぞれ$km\quad kn$とおける
それぞれの正方形の面積は
$\begin{align}km\times km&=k^2m^2\quad&①\\kn\times kn&=k^2n^2\quad&②\end{align}$
となる

①②より面積比は
$k^2m^2:k^2n^2=m^2:n^2\quad③$
←$k^2$は共通しているので割れる
③は相似比の2乗になっている
したがって面積比は相似比の2乗の関係にある
やってることは面積を文字で表して比を確認しただけなので至って単純です。
でも文字で表すと読むのもウンザリするほど難解に感じますね。
繰り返しますが、
面積比は相似比の2乗に等しくなる
これが最優先事項として覚えておきたいものです。
理由についてはある程度余裕が出てきたときに改めて確認するようにしてください。
ところで次のような疑問を持った人もいると思います。
「面積比は相似比の2乗に等しくなることは解った。一般的なことを説明するために文字を使うことも解った。
でもどんな図形にもいえると冒頭に書いてあったけど、今説明にあったのは正方形だけだよな、えぇ?
これじゃ全ての図形について説明したことになってないだろうがっ! どういうことだっっ!!あぁっ!!」

そう疑問を持ったキミは鋭い!!
そう、確かに上記では正方形について確認しただけだから、正方形の場合のみの説明になってます。
でも結論をいうと、やっぱり全ての図形に対して面積比は相似比の2乗に等しくなることがいえるのです。
ならばどうして全ての図形に対していえるのか?
このことを完璧に証明するのはかなりハードなので、簡単な理屈を三角形をもとに紹介します。
なぜ面積比と相似比の関係が全ての図形に対していえるのか
三角形について
三角形が説明の基礎になるので、まず相似比$m:n$の三角形で確認します。
底辺を$k$とすると、底辺の長さはそれぞれ$km$、$kn$と表せます。
同様に高さを$h$とすると、それぞれ$hm$、$hn$と表せます。
このとき面積はそれぞれ
$\dfrac{1}{2}hkm^2,\:\dfrac{1}{2}hkn^2\:$となるため、
面積比は$m^2:n^2$となります。
これを踏まえ多角形の話に移ります。

多角形について
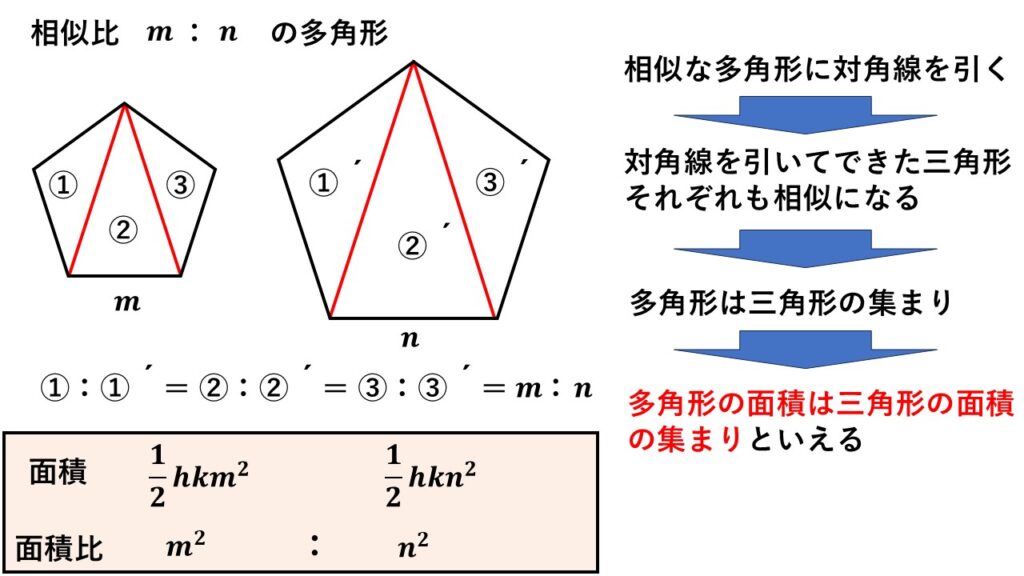
多角形は対角線を引くことで三角形に分けることができます。
言い方を変えると、多角形は複数の三角形が集まってできた図形と解釈できます。
ということは、
相似比$m:n$の2つの多角形があったとき、
対角線を引いてできる三角形もそれぞれ相似となり、対応する三角形の相似比も$m:n$となる
ことがいえます。
さらに多角形は三角形の集まりなので、その面積も三角形の面積を足したものと考えられ、計算上$\dfrac{1}{2}hkm^2$と$\dfrac{1}{2}hkn^2$として表せます。
これより面積比は
$m^2:n^2\:$となるわけです。
円について
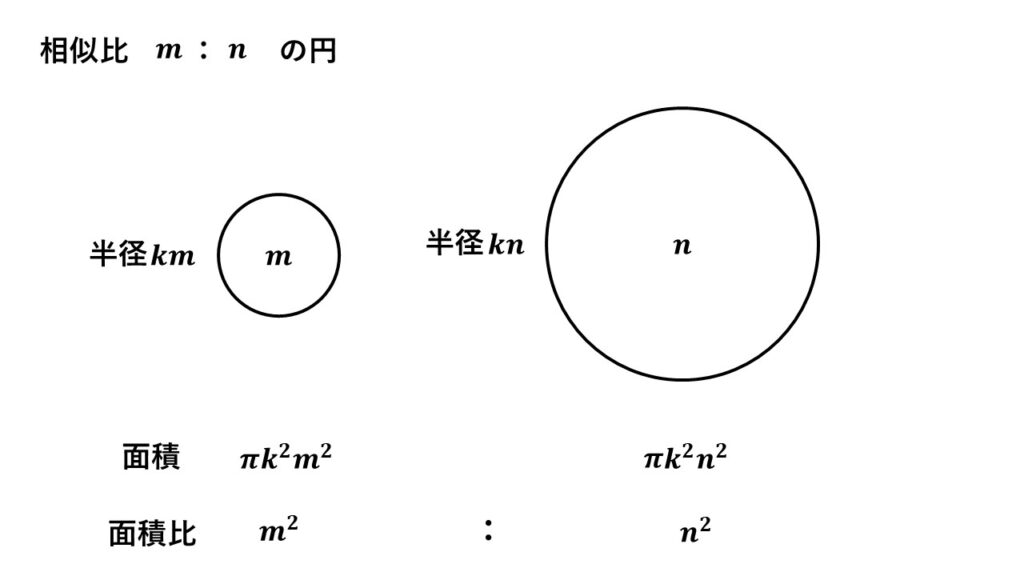
円も同様に説明できます。
$k$を半径とすると相似比$m:n$の円の半径はそれぞれ
$km,kn$とおけます。
すると面積はそれぞれ
$\pi k^2m^2$と$\pi k^2n^2$となり
やはり面積比は
$m^2:n^2$となります。
このように文字を使った計算式で説明すると、理屈上どんな図形に対しても相似比と面積比の関係をいえるわけです。
ここまで三角形、多角形、円と解説しましたが、名もないような図形でも同様です。
例えば相似なソーセージ。
これ、図形の名前はたぶんないと思いますが、この形も面積を求めることができます。
するとやはり結果的に相似比の2乗が面積比となります。

名もない図形の面積については中学数学の範囲を大きく超えるのでここでは割愛します。ただ、この世にある最高に性能の良い顕微鏡で見てようやく判るくらいのものすごーーーーーーーーーく小さい三角形がたくさん集まると、限りなくソーセージの形に近くなっていきます。
相似比と面積比の基本例題
基本例題1
2つの相似な図形で相似比が$2:3$のとき、周の長さの比と面積の比を求めよ。
考え方
周の長さとはその図形の周りの長さ、輪郭の長さのこと。
相似比は長さをもとに比で表したのもなので、周の長さを考えたところで相似比が変わることはありません。
解答
周の長さの比 $2:3\quad$面積比$4:9$
基本例題2
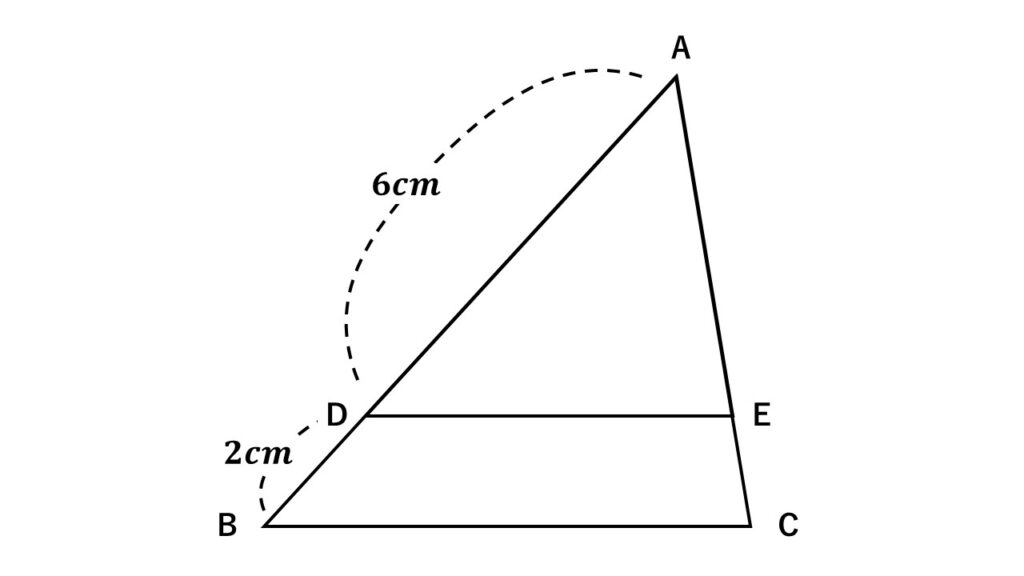
図は$DE//BC$である。
$(1)\:\triangle ADE$と$\triangle ABC$の面積比を求めよ。
$(2)\:\triangle ADE$の面積が$27cm^2$のとき、$\triangle ABC$の面積を求めよ。
$(3)\:$四角形$DBCE$の面積を求めよ。
考え方
$(1)\:\triangle ADE$と$\triangle ABC$は相似です。相似比を確認しましょう。
$(2)\:$面積比は相似比の2乗であることを比例式で表しましょう。
$(3)\:\triangle ABC$の面積から$\triangle ADE$の面積を引けば四角形$DBCE$の面積が求まります。
解答
$(1)\:\triangle ADE\backsim\triangle ABC$で
$\quad AD=6cm,AB=6+2=8cm$より
相似比は$3:4$
よって面積比は$9:16$
$(2)\:\triangle ABC$の面積を$x$とする
$\quad(1)$の結果より
$\begin{align}\quad9:16&=27:x\\9x&=432\\x&=48\end{align}$
よって$\triangle ABC$の面積は$48cm^2$
$(3)\:48-27=21$より四角形$DBCE$の面積は$21cm^2$
$(3)$別解
四角形$DBCE$の面積を$y$とする
$\quad\triangle ADE$と$\triangle ABC$の面積比が$9:16$より
$\triangle ABC$と四角形$DBCE$の面積比は
$\quad16:(16-9)$より$16:7$
これより
$\begin{align}\quad16:7&=48:y\\16y&=336\\y&=21\end{align}$
解説
基本例題1はノーヒントで正答できないと、ちょっともう・・・、やばいです。
基本例題2の$(1)$と$(2)$も絶対正答できないといけません。
$(3)$は2つの三角形の面積を求めてから引き算して四角形の面積を求めました。
別解ではまず四角形の面積比を表して、そこから比例式の関係にもっていきました。
基本例題2では解答の進め方が解きやすいですが、別解の解き方も理解しておきましょう。
ところで、$(2)$は$(3)$を解くためのヒントになっていましたが、それに気づいた人も多いと思います。
少しレベルの上がった定期テストや高校入試では、図と$\triangle ADE$の面積があるだけで、いきなり四角形の面積を求めさせる出題もあり得ます。
この基本例題2で解き方の流れを理解しましょう。
なお、そこからさらに発展させて、点$C$から$AB$までの距離を求めさせる出題もできます。
入試では「点$C$から$AB$までの距離を求めさせる」ことが本当の出題の意図だったりもします。
$\triangle ABC$の$AB$を三角形の底辺とみなし、面積が分かっていれば距離つまり高さを求められますね。
1つ1つ順を追って解いていけばどうということはありませんが、図と$\triangle ADE$の面積$27cm^2$が与えられていきなり「点$C$から$AB$までの距離を求めよ」と出題されたら、さすがに難易度爆上がりです。
でも入試ではそのようなことも考えらます。
基本例題2を何度も確認して解き方の流れを理解しておきましょう。
