一次関数の式を求める問題　パターン別解法

一次関数の式を求める問題は中学数学の中でも特に重要度が高く、定期テストや高校入試でも必ず出題されます。
その一次関数の式を求める問題にはいくつかの出題パターンがあります。
ということは、出題パターンを覚えてしまえばテストの得点源にもなるということ。
ここでは一次関数の式の求め方をパターン別に紹介し、解き方を徹底して身につけていきます。

一次関数の式を求める大前提

一次関数の式を求める問題のほとんどは『一次関数の式を求めよ』と書かれています。そのため、

必ず　$y=ax+b$　と置いてから解き始めること。

これは全ての問題パターンの大前提。
問題文中に手がかりがあるのでそれをもとに$a$や$b$の数値を求め、その値を当てはめて式を答えます。
それでは実際に問題を通して理解していきましょう。

パターン1　変化の割合とグラフが通る点がある

変化の割合とグラフが通る点が与えられているパターンは、一次関数の式を求める問題全ての土台になっています。
とにかく解き方を覚えてください。

基本例題1
変化の割合が$3$で、点$(2,7)$を通る一次関数の式を求めよ。

考え方
これは最も初歩的なパターンの問題です。絶対にできるようにしておきましょう。
「一次関数の式を求めよ」とあるので必ず、
$y=ax+b$　と置いてから解答を進めます。
変化の割合が$3$なので$a=3$
$(2,7)$を通るので$x=2$　$y=7$　を代入し$b$の値を求めます。

解答
求める一次関数を　$y=ax+b$　とする
$\begin{align}7&=3\times2+b\\7&=6+b\\b&=1\end{align}$
よって　$y=3x+1$

補足
一次関数では変化の割合と傾きは同じことを表しています。
そのため
『傾きが$3$で、点$(2,7)$を通る一次関数の式を求めよ』
と出題されても解き方は同じです。

基本例題2
グラフが$y=4x-2$に並行で、点$(2,3)$を通る一次関数の式を求めよ。

考え方
この問題も「変化の割合とグラフが通る点がある」パターンの問題です。
「平行」がこの問題のポイント。
グラフが平行ということは、グラフの傾きが同じということ。
つまり変化の割合が同じ値であるということ。
よって基本例題1と解き方は同じです。

解答
求める一次関数を　$y=ax+b$　とする
求める一次関数のグラフが$y=4x-2$に並行なので変化の割合は$4$
そして点$(2,3)$を通るから
$3=4\times2+b$
$3=8+b$
$b=-5$
よって　$y=4x-5$

パターン2　切片とグラフが通る点がある

このパターンも解き方はパターン1とほぼ同じです。

基本例題3
グラフの切片が$-2$で点$(4,3)$を通る一次関数の式を求めよ。

考え方
切片がわかっているので、$y=ax+b$の$b$に切片の値を代入して求めます。

解答
求める一次関数を　$y=ax+b$　とする。
点$(4,3)$を通るから
$3=a\times4+b$

$5=4a$
$a=\dfrac{5}{4}$
よって　$y=\dfrac{5}{4}x-2$

解説
基本例題を3つ扱いましたが、全ての基本がこの3問に詰まっています。
$y=ax+b$と置いたら$a$や$b$を求めて当てはめる。
この解き方の流れをしっかり覚えておきましょう。

パターン3　条件から変化の割合を算出して一次関数の式を求める

ここからはひと手間加えてから一次関数の式を求める問題を扱います。
「$y=ax+b$と置いたら$a$や$b$を求める」ことをふまえ、問題を見ていきましょう。

基本例題4
$x$が$3$増加すると$y$は$4$減少し、$x=-3$のとき$y=2$となる。このときの一次関数の式を求めよ。

考え方
$y=ax+b$　と置いて進めていくことに変わりはありません。
ただ変化の割合も切片も問題に書いてないので、そのまま数値を代入して解くことができません。
ここで注目するのが『$x$が$3$増加すると$y$は$4$減少し』のところ。
これが変化の割合を示しています。
$変化の割合=\dfrac{yの増加量}{xの増加量}$
この関係式を使って変化の割合を求め、$y=ax+b$に当てはめます。
すると切片も求められます。

解答
求める一次関数を　$y=ax+b$　とする。

パターン4　グラフの通る点が2点与えられている

基本例題5
座標平面上の$2$点$(-1,4)$と$(2,-2)$を通る一次関数の式を求めよ。

考え方
$y=ax+b$と置いたうえで$a$と$b$を求めます。
$(-1,4)$を通るときと、$(2,-2)$を通るときそれぞれについて式を作ります。
すると式が$2$つ作れるので、連立方程式として解くとで$a$と$b$が求められます。
あとは$y=ax+b$に当てはめれば求められます。

解答
求める一次関数を$y=ax+b$とする。
点$(-1,4)$を通るので
$4=-a+b$　①
点$(2,-2)$を通るので
$-2=2a+b$　②
①②を連立方程式として解くと
$\begin{cases}\begin{align}4=-a+b　&①\\-2=2a+b　&②\end{align}\end{cases}$
①－②より
$6=-3a$
$a=-2$
$a=-2$を①へ代入
$4=2+b$
$b=2$
よって求める一次関数は
$y=-2x+2$

解説
2点が与えられたパターンの問題でも冒頭に書いた通り、$y=ax+b$と置いて$a$と$b$を求めます。
$a$と$b$を求めるために連立方程式を作ったというわけです。
とにかく一次関数の式を求める問題では、$a$と$b$を求めるために色々と策を講じると覚えておきましょう。

ところでこの2点が与えられたパターンの問題は別の解き方もあります。
別解は以下のようになります。

別解

求める一次関数を$y=ax+b$とする。
2点$(-1,4)$と$(2,-2)$を通ることより変化の割合を求められる。

$変化の割合＝\dfrac{yの増加量}{xの増加量}$より

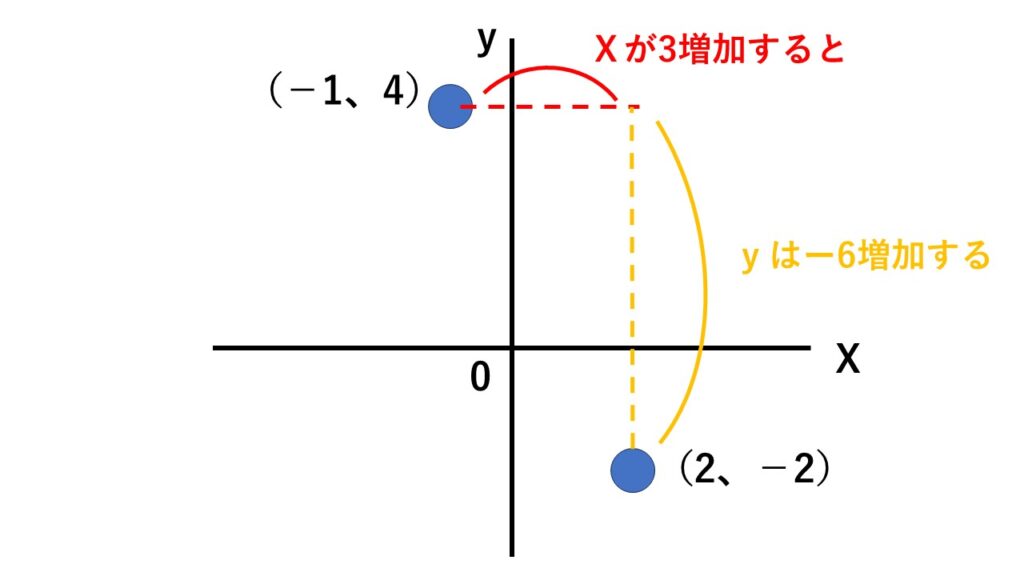
$\begin{align}変化の割合=\dfrac{-2-4}{2-(-1)}\\=\dfrac{-6}{3}=-2\end{align}$
よって$y=-2x+b$

これが$(-1,4)$を通るから
$\begin{align}4&=-2\times(-1)+b\\4&=2+b\\b&=2\end{align}$

←$x=2,y=-2$を代入しても良い

よって求める一次関数は
$y=-2x+2$

解説
2点を通ることから変化の割合がわかります。
変化の割合がわかれば後は$b$を求めるだけ。
$b$を求めるために、通る点のどちらかを使えば良い。
という流れです。
連立方程式を使う方法、別解の方法、どちらの方法も解き方の流れを理解しましょう。
変化の割合を求められれば、パターン1と同じ解き方になることを確認してください。