
一次関数$y=ax+b$のグラフは
$a>0$のとき右上がりの直線
$a<0$のとき右下がりの直線
として表せる
いきなりPOINTから入りましたが、とても重要な事柄です。一次関数のグラフを考えるときは$a$の値に注目します。
なぜ$a$(変化の割合)に注目していくのか、まずはそこから理解していきましょう。
『一次関数のグラフ』と言われるといかにも難しそうな感じがしますが、その特徴さえ知ってしまえば何ら難しいことはありません。
冒頭のPOINTは重要なので後でまた載せますが、ひとまず一次関数のグラフは直線になるということをおさえておいてください。
一次関数のグラフの特徴
一次関数のグラフは$a$の値が正か負かによって、グラフが伸びていく方向が変わります。
ということで$a$が正の値のときの例として$2$を、負の値のときの例として$-2$を見ていきます。
$y=2x-3$の特徴
変化の割合が$2$、つまり$a$の値が$0$より大きい($a>0$)ことに注目してください。
$x$に適当に値を代入すると、それに対応する$y$の値は以下の表のようになります。
| $x$ | ・・・ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | ・・・ |
| $y$ | ・・・ | $-9$ | $-7$ | $-5$ | $-3$ | $-1$ | $1$ | $3$ | ・・・ |
当然ですが、変化の割合が示す通り$x$の値が$1$ずつ大きくなると、$y$の値は$2$ずつ大きくなります。
この関係を座標平面上に表していきます。
$(-3,-9) 、(-2,-7) 、(-1,-5) 、(0,-3) 、(1,-1)、 (2,1) 、(3,3)$がグラフの通る点です。
点が座標平面上にズラッと並びましたが、一直線上に並んでいることがわかります。そして右上がりに点が並んでいることがわかります。

この点の並びと変化の割合の意味を関連付けて理解してください。
すると$a>0$のときは右上がりのグラフになるのは当然なわけです。
※ 直線は非常にたくさんの点が集まってできたものです。例では$x$の値を整数のときだけで計算しましたが、小数まで含めてより細かく見ていくと、点の集まりが直線になっているとわかります。
$y=-2x+3$の特徴
変化の割合が$0$より小さい($a<0$)であることに注目してください。
| $x$ | ・・・ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | ・・・ |
| $y$ | ・・・ | $9$ | $7$ | $5$ | $3$ | $1$ | $-1$ | $-3$ | ・・・ |
「$x$の値が$1$ずつ大きくなると$y$の値は$-2$ずつ大きくなる($2$ずつ小さくなる)」ことがわかります。
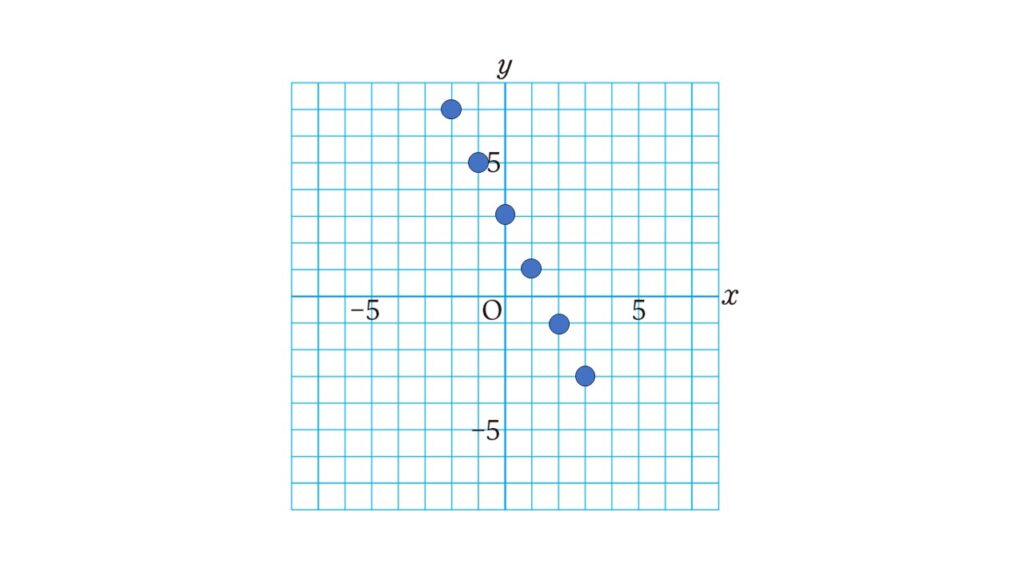
$(-3,9) 、(-2,7) 、(-1,5) 、(0,3) 、(1,1)、 (2,-1) 、(3,-3)$がグラフの通る点です。
右下がりに点が並んでいることがわかります。
$a>0$のときは右上がりのグラフ
$a<0$のときは右下がりのグラフ
と、なんの脈略もなく言われると意味不明かもしれません。でも$x$に数値を代入して$y$の値を求め、その結果を座標平面上に点にして表していると考えれば、決して難しいことをいっているわけではありません。

一次関数$y=ax+b$のグラフは
$a>0$のとき右上がりの直線
$a<0$のとき右下がりの直線
として表せる
一次関数のグラフの特徴を知ったら、実際にグラフをかけるようにしましょう。
一次関数のグラフのかき方
超基本パターン

一次関数のグラフ かき方の手順 超基本パターン
- グラフが通る点を適当に2か所計算で求める
- 求めた2点をまっすぐな線で結ぶ
これが一次関数のグラフをかく手順です。この手順が全ての超基本になります。たった2つです。
2つだからもう覚えましたよね。
早速かいてみましょう。
基本例題1
一次関数$y=3x-1$のグラフをかけ。
考え方
①グラフが通る点を適当に求めます。
$x$に何でも良いので数値を代入し、そのときの$y$の値を求めます。
$x$はまぁ小さい数値の方が良いですよね、計算しやすくて。
それを2か所分求めます。
ここでは$x=-1$と$x=1$のときを計算してみます。
②2点をまっすぐな線で結んで終わり。
解答
$x=-1$のとき
$y=3\times(-1)-1=-4$
$x=1$のとき
$y=3\times1-1=2$
これより$(-1,-4)$と$(1,2)$を通るのでグラフは図のようになる。

どうです? 計算ミスさえしなければどうということは無いですよね。
まずは超基本となる2点を求めて線で結ぶ方法を理解しましょう。
ところで超基本と何度も強調してますが、「超基本じゃない方法があるのか!!」と考えた人もいると思います。
で、実際超基本じゃないパターンはあります。
ということで次に基本パターンのかき方を見ていきます。基本パターンはちょっとだけラクできます。
基本パターン
一次関数$y=ax+b$の$b$のことを切片といいました。
切片は$x=0$のときの$y$の値、つまりグラフが通る$y$軸上の点を示しています。
ということは、切片$b$を見れば計算するまでもなくグラフが通る点の1つがわかるのです。
そのため、通る点を1つ計算で求め、それを切片とまっすぐな線で結べば完了。
計算が1回で済むからラクですね、少しだけど。

一次関数のグラフ かき方の手順 基本パターン
- グラフが通る点を適当に1か所計算で求める
- 切片とグラフが通る点をまっすぐな線で結ぶ
基本パターンもしっかり理解しておきましょう。
ただ、基本パターンも結局のところ超基本パターンと同じことをやっています。
もう一度同じ例題を使ってグラフをかいてみます。
基本例題1-2
一次関数$y=3x-1$のグラフをかけ。
解答
$x=3$のとき
$y=3\times3-1=8$
これより$(3,8)$を通る
また切片が$-1$なので
$(0,-1)$を通る
よってグラフは図のようになる

ラクですよね。ラクだから楽しいでしょ?
何だったらもうちょっとラクしたいですよね?
ということで、もうちょっとラク(横着)できるグラフのかき方があります。
横着パターンも学んでおきましょう。
横着パターン
横着パターンでは変化の割合の性質に着目します。
$\dfrac{yの増加量}{xの増加量}$
つまり、$x$が$1$増えると$y$がいくつ増えるか、を読み取り、グラフが通る点に印をつけていきます。
ということで変化の割合に不安がある人は、冒頭に紹介したページで確認してくださいね。
例えば、変化の割合が$2$とあったら、
$x$が$1$増えると$y$は$2$増える ということでした。
変化の割合が$-2$とあったら、
$x$が$1$増えると$y$は$-2$増える($2$減る)ということでした。
いいですか? 大切なことなので繰り返しますが、この関係を使ってグラフをかきます。

一次関数のグラフ かき方の手順 横着パターン
- 切片に印をつける
- 変化の割合に注目し、印をつける
- 2つの印をまっすぐな線で結ぶ
横着パターンでは計算しません。式を見ただけでグラフが通る点を判断します。
さあ、ここで頭を働かせてください。
切片はグラフが通る点だということは既に紹介した通り。
変化の割合も結局のところ、グラフが通る点を示しているわけです。
つまり、横着パターンも行きつくところは超基本パターンと同じで、グラフが通る点を2か所求めることになります。
ということでここまでを簡単にまとめると、
超基本パターンの理屈は必ず理解してください。これがグラフをかく大前提です。
これを理解すると基本パターンでのかき方の意味が理解できる。
基本パターンを理解してから横着する。
ということになります。
いきなり横着するのはダメです。ちょっと努力してから横着しましょう。
それでは横着パターンを使ってグラフをかいてみます。
基本例題1-3
一次関数$y=3x-1$のグラフをかけ。
考え方
切片が$-1$なので$(0,-1)$を通ります。
そして変化の割合$3$に注目します。
$\dfrac{yの増加量}{xの増加量}$が$3$。もう少し細かく書くと
$\dfrac{yの増加量}{xの増加量}=3=\dfrac{3}{1}$
$x$が$1$増えると$y$が$3$増える点をグラフが通る、ということ。
つまり切片から数えて、右へ$1$、上へ$3$進んだ点がグラフの通る点になります。

解答
$(0,-1)$と$(1,2)$をまっすぐな線で結ぶ。

一次関数のグラフ 分数を含むタイプ
ここから先は、超基本パターン、基本パターン、横着パターンをしっかり理解したら読んでください。
初めに書いておきますが、分数を含む一次関数でも超基本パターンの考え方を使えば、必ずグラフをかくことができます。ただ分数を含むと計算が少し面倒。
ということで分数を含む一次関数のグラフを、横着パターンでかいてみましょう。
基本例題2
一次関数$y=\dfrac{2}{3}x-2$のグラフをかけ。
考え方
変化の割合が分数でも既に紹介した書き方と同じです。
切片が$-2$なので$(0,-2)$を通ります。
そして変化の割合に注目します。
$\dfrac{yの増加量}{xの増加量}$が$\dfrac{2}{3}$です。
つまり、今ある点から見て、$x$が$3$増えら$y$が$2$増える点をグラフが通ることを表しています。

解答
$(0,-2)$と$(3,0)$を通るグラフになる。

補足
分数を含む一次関数のグラフを難しく感じている中学生が多いようです。
座標に分数にあたる目盛りがないことが理由でしょう。
ただ、変化の割合の性質に注目すれば計算することなくグラフが通る点が求まるので、1か所だけ通る点がわかれば横着できます。
切片が整数ならば計算するまでもなく、通る点が1つわかります。
ただ切片が分数や小数の場合は、計算しないと通る点がわかりません。
見た目や直感でグラフが通る点を判断して印をつけたら、正確なグラフになりません。
例えば$y=\dfrac{1}{3}x-\dfrac{11}{3}$のグラフをかくとき、切片が分数なので、座標平面上に正確に通る点の印をつけることはできません。

切片が分数や小数で表されているときは、残念ながら横着パターンでグラフをかくことはできません。
超基本パターン、つまり通ると確実にわかる2点を地道に計算で求め、その2点をまっすぐな線で結んでいきます。

