方程式の文章題 過不足

方程式の過不足問題もテストでよく出題されます。ここでは過不足問題の考え方を超基本から徹底して攻略していきます。それではまずウォーミングアップとして超基本の確認から。

余る時と不足する時の式

超基本から徹底するので簡単すぎると甘く見るのではなく、新鮮な気持ちで受け入れてください。

超基本例題1　みかんを5人に3個ずつ配ると2個余る。みかんは何個ありますか。

ぶっちゃけ簡単ですよね？　小学生でもわかるって思いますよね。確かにそうです。小学生が学ぶ問題です。でもこの簡単すぎることが、方程式の文章題になるとなぜか難しく思えてしまうのです。

答えは　$3\times5+2=17$　で$17$個です。
1人あたりの個数に人数をかけて余りを足すと、みかん全部の個数が出ます。

超基本例題2　みかんを6人に3個ずつ配ると1個不足する。みかんは何個ありますか。

これも簡単だと思います。でもやっぱり方程式の文章題になると難しく思えてしまいます。

答えは　$3\times6-1=17$　で$17$個です。
1人あたりの個数に人数をかけて不足分を引くと、みかん全部の個数が出ます。

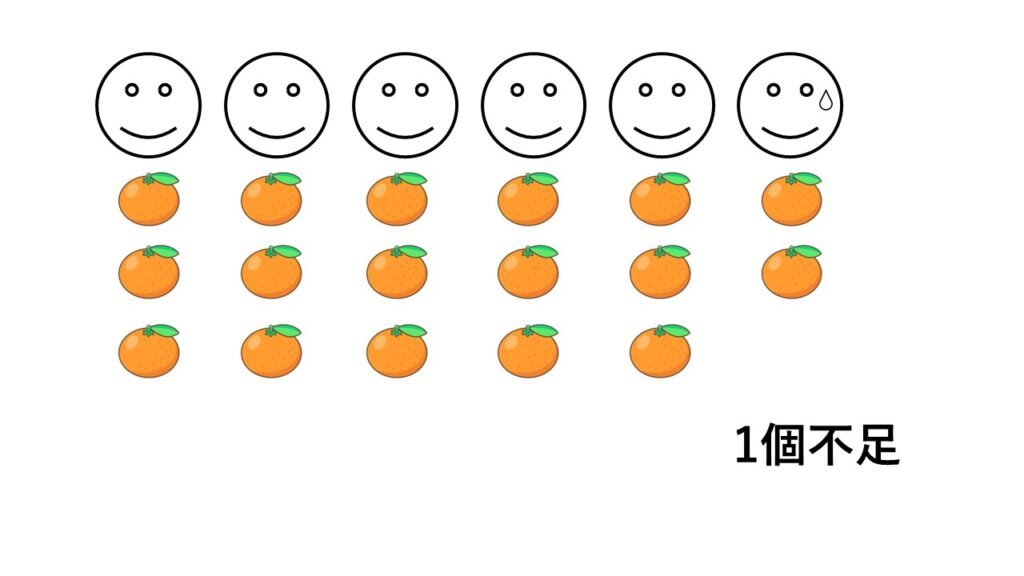
超基本例題3　21個のみかんを1人に3個ずつ配ると、何人に配れますか。

これも大丈夫ですよね。
みかんの総数を1人あたりの個数で割れば人数がわかります。
答えは　$21\div3=7$　で$7$人です。

超基本例題4　22個のみかんを1人に3個ずつ配ると、何人に配れますか。

答えは　$22\div3=7$あまり$1$　でやはり$7$人です。

通常は7人と答えて正解なのですが、次のような解釈もできてきます。
ややこしい話ですが付いてきてくださいよ。

「1人3個」をきっかり守るのなら確かに7人です。
でも「不足しても良いからとりあえず最大限の人数に配る」ということなら8人といえます。
つまり7人は3個ずつだけど、1人は1個という解釈。
すると8人目の人は「2個不足している状態」といえます。

ならばもし、あらかじめ2個不足するということがわかっていたら、もともとある個数に不足分の2個を足して、その数を1人分の個数で割ると人数のみがガツンと求められます。

超基本例題を4つ載せましたが、これらの考え方が方程式の過不足の問題では重要になってきます。
特に超基本例題4は、このページの最後に紹介する解答方法で大切な考え方になるので、頭の片隅にちょこっと置いておいてください。

それではこれらをふまえ本題に入っていきます。

みかんを配る時の過不足　基本例題

方程式の文章題を解く手順を確認しておきます。

1. ふつう求めるものを$x$とする
2. 数量関係に注意して方程式を作る
3. 作った方程式を解く
4. 求めた解が正しいか確かめる

基本例題　みかん愛好家にみかんを配るのに、1人に5個ずつ配ると4個余り、1人に7個ずつ配ると6個不足します。みかん愛好家は何人いますか。

考え方　過不足の問題を難しく感じてしまう原因に「わからない事柄が2つある」ということがあります。
この例題でいうと「みかんの個数」と「みかん愛好家の人数」の2つがわかりません。
わからない事柄が2つあるから、何を式として表せばよいのかが見えにくくなってしまうのです。

ここで冒頭の超基本例題1と2を振り返ってください。
「5人に3個ずつ配ると余るor不足する時のみかんの個数」を考える問題でした。
みかんの個数を表す式を作りましたよね。
それと同じく、この基本例題でもみかんの個数を表す式を作っていきます。

そのためにはみかん愛好家の人数がわからないと式を作れません。
ただ、この問題の求めるものはみかん愛好家の人数。
ならば、その求める「みかん愛好家の人数」を$x$として式を作れば良い、ということになります。

1人に5個ずつ配ると4個余るからみかんの個数は
$5x+4$　個と表せる。

1人に7個ずつ配ると6個不足するからみかんの個数は
$7x-6$　個と表せる。

これより
$5x+4=7x-6$

$5x-7x=-6-4$

$-2x=-10$

$x=5$

よって、みかん愛好家は5人いる

補足　みかん愛好家が5人とわかれば、みかんの個数もわかります。
$5\times5+4=29$　もしくは
$7\times5-6=29$　で29個と求まります。

●目のつけどころ●

数値としての手がかりがない事柄を式にすれば、上手く方程式を作れることがあります。

この基本例題では、
みかんの個数　か　みかん愛好家の人数　
になりますが、解答ではみかんの個数を表す式を作って方程式を立てました。

多少複雑になりますが、みかん愛好家の人数を表す式を作る方法もあります。
ただこの方法の場合、求めるものを$x$とすると式を作れません。
だってそうですよね。みかん愛好家の人数の式を作るのにそれを$x$としたら、式を作ろうにも作れません。つまり
「方程式の文章題を解く手順①　ふつう求めるものを$x$とする」に反してしまいます。
なので「みかん愛好家の人数を表す式を作る方法」では、また別のことを$x$としなければなりません。

ならば何を$x$とするか？

ということで、みかんの総数を$x$とし、みかん愛好家の人数を表す式を作って解いてみます。
なお上記解答とは別の方法なので、あえて文字を$x$ではなく$m$としていきます。

人数を式で表す解き方

では改めて問題から。

基本例題　みかん愛好家にみかんを配るのに、1人に5個ずつ配ると4個余り、1人に7個ずつ配ると6個不足します。みかん愛好家は何人いますか。

1人に5個ずつ配ると4個余るから
みかんの総数から4を引いた数を5で割ると
割り切れて、なおかつ人数を表せるので、
愛好家の人数は
$\dfrac{m-4}{5}$　･･･①となる。

1人に7個ずつ配ると6個不足するから
みかんの総数に6を足した数を7で割ると
割り切れて、なおかつ人数を表せるので、
愛好家の人数は
$\dfrac{m+6}{7}$　･･･②となる。

したがって
$\dfrac{m-4}{5}=\dfrac{m+6}{7}$

$7(m-4)=5(m+6)$

$7m-28=5m+30$

$7m-5m=30+28$

$2m=58$

$m=29$

これよりみかんの総数は29個とわかった。
よって$m=29$を①に代入して
$\dfrac{29-4}{5}$＝$\dfrac{25}{5}$　となり
みかん愛好家は5人いる。

●①と②の式ができる理由●

式①と②は人数を表す式でした。
この人数の式を作る時に厄介なのが「余りや不足の扱い方」です。
この余りや不足の扱い方について補足します。

【①の式ができる理由】
みかんの総数を1人あたりに配る個数で割ると、何人に配れるかがわかります。
例えば
「20個のみかんを1人5個ずつ配ったら余ることなく全員に配れた。人は何人いますか」
といわれたら、
$20\div5=4$　（人）と出ますよね。では、

「23個のみかんを1人5個ずつ配ると何人に配れますか」
といわれたらどう考えるか。
$23\div5=4$あまり$3$
となり4人に配れて3個余ることがわかります。

ここで注意しなければならないのが、
単純に23個のみかんを分けて人数を求めることだけを考えるなら
$23\div5=4$あまり$3$　（または$4.6$）
を計算すれば良いのです。すると4人とわかりますから。
ただ方程式として考える時は工夫が必要になります。
方程式は等しい数量関係を＝で結ばないと解けません。


基本例題の別解では、みかんの個数自体が何個かわかりません。なので$m$としたわけです。
しかしここで困った事態が起こります。
$m\div5=$としたところで、これはこれ以上計算しようがないので商も余りも表現できないのです。
つまり方程式を作れないのです。

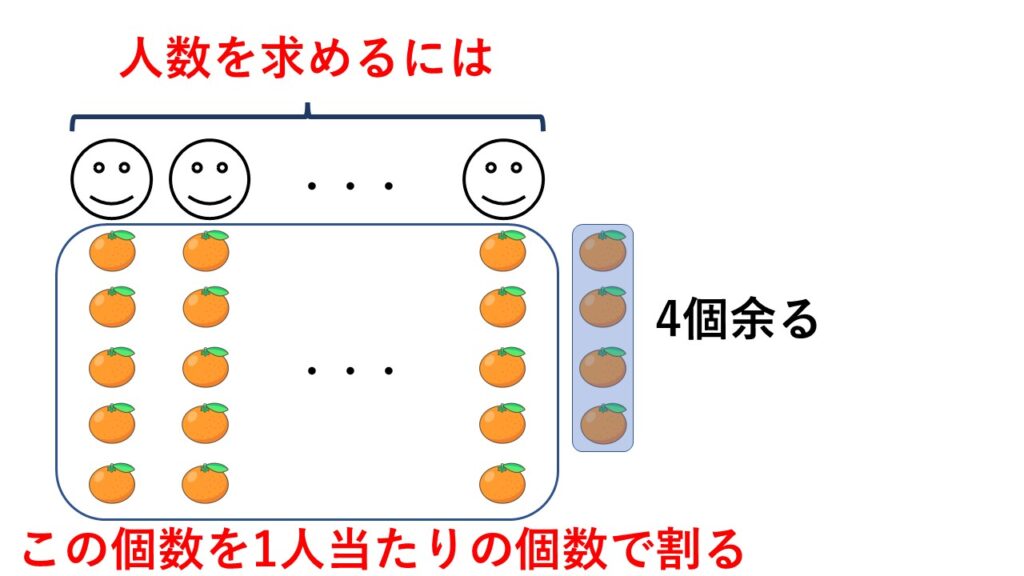
そこで余りに注目します。
もしあらかじめ余りの個数がわかっていたら、みかんの総数から余りの分を先に引いて、引いた数を1人あたりの個数で割れば、人数のみが数値として出ます。
$(23-3)\div5=4$　という感じで。
いいですか。人数を表す式を作るのが別解の解き方だから、余りが出ない人数のみを表す式が必要なのです。

この考え方を使ったのが別解の①の式です。
つまりみかんの総数$m$からあまりの分4を先に引いて、1人あたりの個数で割ったものが①の式です。

【②の式ができる理由】

②式では、最後の1人は7個もらえないので、単純に$m$個を1人分の7で割ることができません。
ここで人数を表す式づくりの工夫が必要になります。つまり
みかんの個数を1人分の7で割った時に、人数のみが数値として出てくるようにする工夫。
その工夫とは超基本例題4で紹介した事柄でズバリ、
最後の1人も7個もらえたと仮定して式を作ります。

実際は最後の1人は1個しかもらえていないですよね。6個不足することが問題文からわかっています。
それを7個もらえていたとみなして考えます。

ということは、みかんの総数$m$個に不足分の6個を加えて$(m+6)$個あるとみなして式を作ります。
そうすることで全員が7個もらえていると考えることができます。

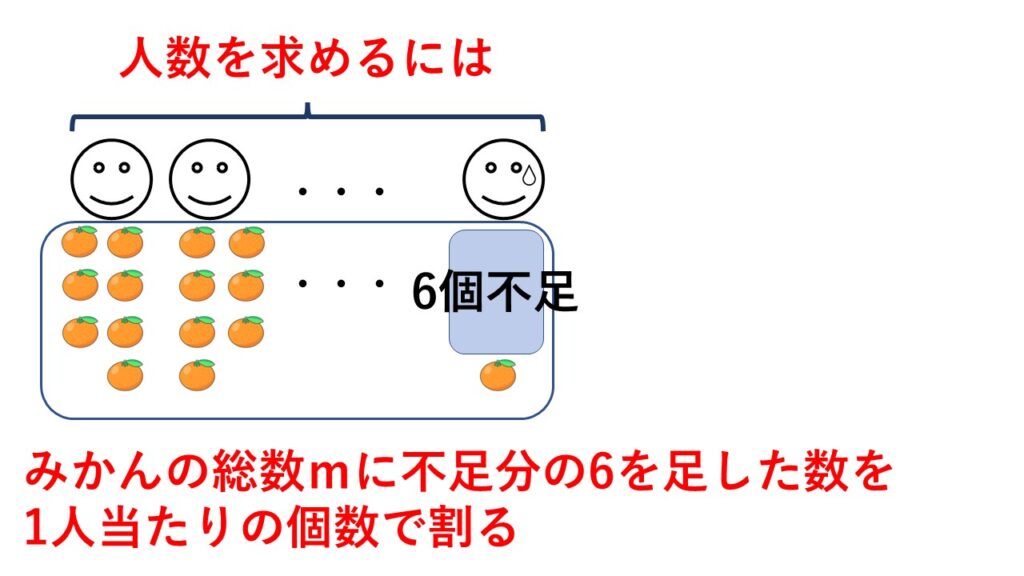
すると　$\dfrac{m+6}{7}$　の式ができ、人数のみが数値として出てきます。

参考
②式の別表現として、
$\dfrac{m-1}{7}+1$　も作れます。

すると方程式
$\dfrac{m-4}{5}＝\dfrac{m-1}{7}+1$
も成り立ちます。

なぜこの方程式でも解けるのか、上のイラストを参考に考えてみてください。