$y=ax^2$のグラフの変化の割合は$x$の区間に注目

$y=ax^2$のグラフの変化の割合は考え方が少し複雑になるので、多くの中学生が一度は悩む分野のようです。
ここでは$y=ax^2$のグラフの変化の割合について基本中の基本から徹底して解説し、理屈で考える力を身につけていきます。

$y=ax^2$のグラフの変化の割合

一次関数で学んだ変化の割合とはざっくりいうと「$x$が1増えたときに$y$はいくつ増えるか」ということで、「グラフの増え方の目安」を表していました。
$x$の範囲によってグラフがどのように増減するのかを数値で考えるのが変化の割合です。

これから学ぶ$y=ax^2$のグラフの変化の割合も同様に「グラフの増え方の目安」を表しています。
そして変化の割合を求める式として、$変化の割合=\dfrac{yの増加量}{xの増加量}$を計算するのも同様です。

ただ一次関数のときとは大きく違う点があります。
では何が一次関数のときと違うのか？

放物線のグラフの変化のしかたを考えたい

変化の割合という用語自体は中2で学んだ一次関数で扱いました。
ということで、変化の割合を完全に忘れてしまっている人はまずこちらを復習してください。

このページでは変化の割合について大まかなことは覚えているのを前提で進めていきます。

一次関数$y=ax+b$では$a$の値がそのまま変化の割合を表していました。
でも関数$y=ax^2$では$a$の値がそのまま変化の割合を表しているということではありません。
そのことを$y=x^2$のグラフを例として理解していきましょう。

いいですか？
重要なので繰り返しますが、

$x$の範囲（区間）によってグラフがどのように増減するのかを考えるのが変化の割合

ですからね。
これから$変化の割合=\dfrac{yの増加量}{xの増加量}$の計算を夢に出てくる位たくさんやるので覚悟してください。

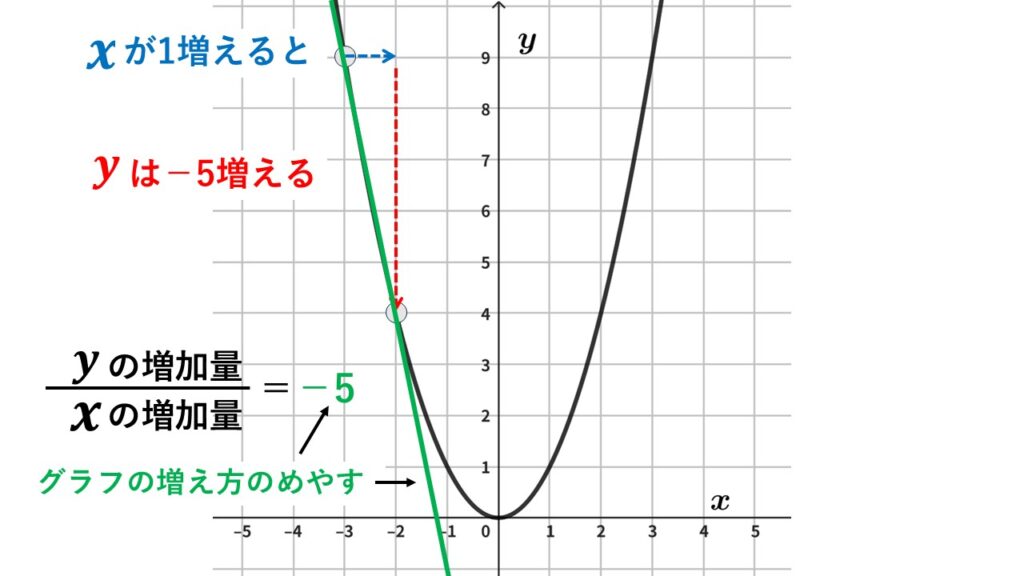
$x$が$-3$から$-2$まで$1$増えたときの変化の割合

$x$が$-3$から$-2$まで$1$増えたとき、$x$の増加量は$-2-(-3)=1$、
$y$の増加量は$(-2)^2-(-3)^2=-5$です。

これより$変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-5}{1}=-5$です。

変化の割合が負の値のとき、その区間では減っていくグラフになります。

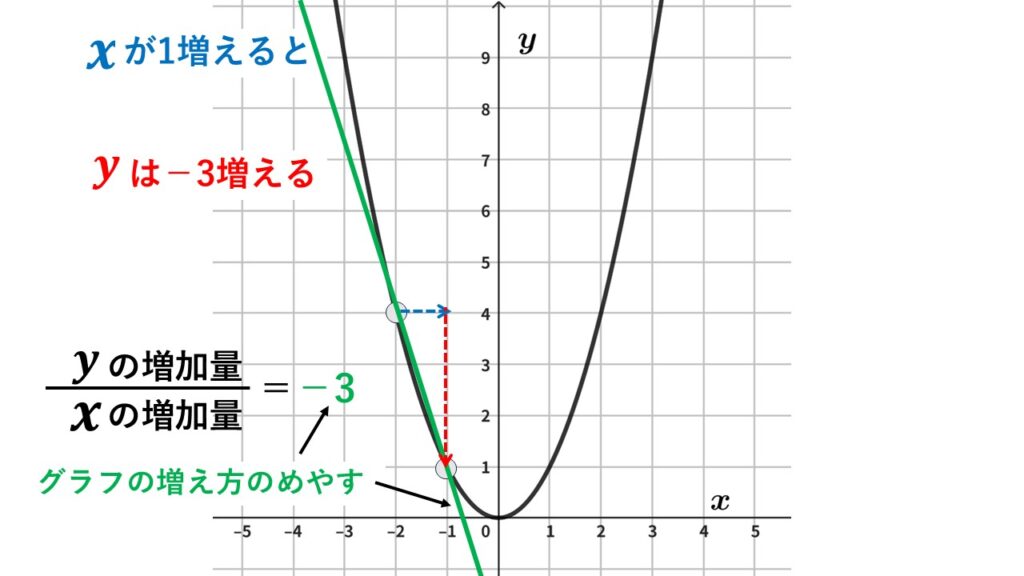
$x$が$-2$から$-1$まで$1$増えたときの変化の割合

$x$の増加量は$-1-(-2)=1$です。
$y$の増加量は$(-1)^2-(-2)^2=-3$です。

これより$変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-3}{1}=-3$です。

ここで変化の割合の値に注目してください。
一次関数の変化の割合は常に一定の値を取り、それが$y=ax+b$の$a$のことでした。
でも今求めた$y=ax^2$のグラフの2つの変化の割合は一定ではなく、異なる値となりましたね。

これが一次関数の変化の割合と大きく違うところで最大のポイント。
$y=ax^2$のグラフの変化の割合は$x$の区間によって変化します。
言い方を変えれば、

$y=ax^2$のグラフは$x$の区間によって増え方や減り方が変化します。

グラフを見れば増え方や減り方が変化しているのはわかるだろ!!　と思うかもしれませんが、それはあくまで見た目の話。
グラフの増え方や減り方を数値で説明しているものが変化の割合ということです。

上のグラフでは緑の直線で表したものが変化の割合です。改めて確認してください。
$x$が$-3$から$-2$まで$1$増えたときの変化の割合は$-5$なので、その区間では結構急激に減っていることがわかります。
$x$が$-2$から$-1$まで$1$増えたときの変化の割合は$-3$なので、その区間ではいくらか緩やかな減り方になっているということがわかります。

もう少し変化の割合を求めてみましょう。
上記に習って変化の割合を実際に計算して求めてみてください。

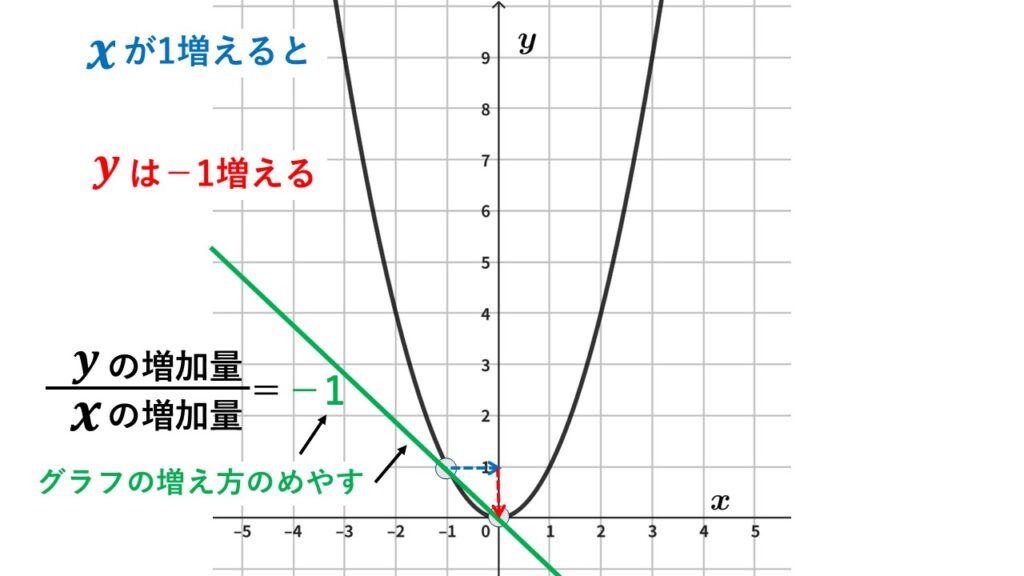
$x$が$-1$から$0$まで$1$増えたときの変化の割合は$-1$

$x$が$-3$から$-2$まで$1$増えたときに比べて、変化のしかたがかなり緩くなっているのがわかります。

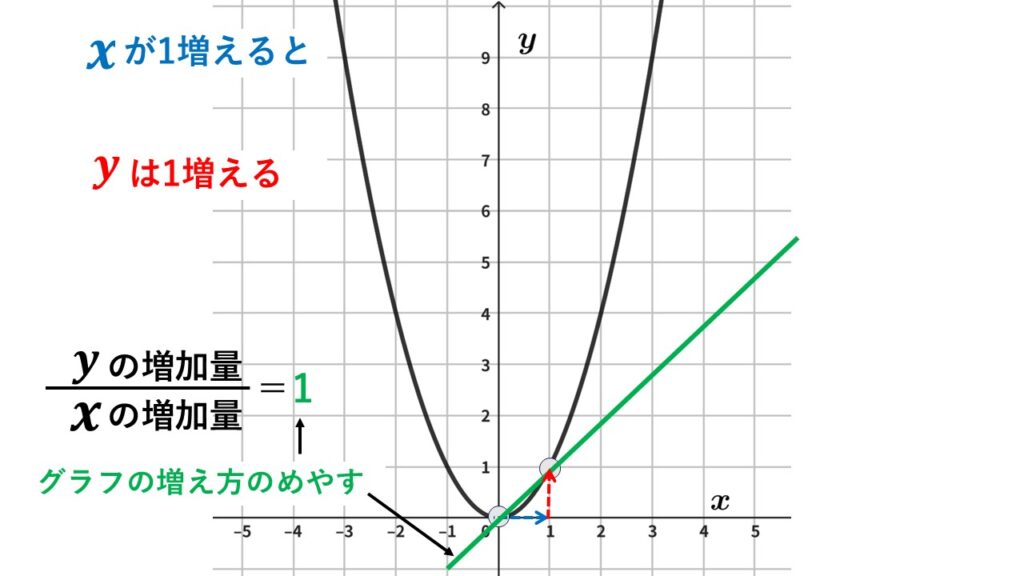
$x$が$0$から$1$まで$1$増えたときの変化の割合は$1$

変化の割合が正の値になったということは、この区間では$y=x^2$は増加しているということを表します。

グラフを見れば原点（放物線の頂点）で負から正に変わっているのは明らかですが、計算でグラフの増減の様子を示すことに大きな意味があります。

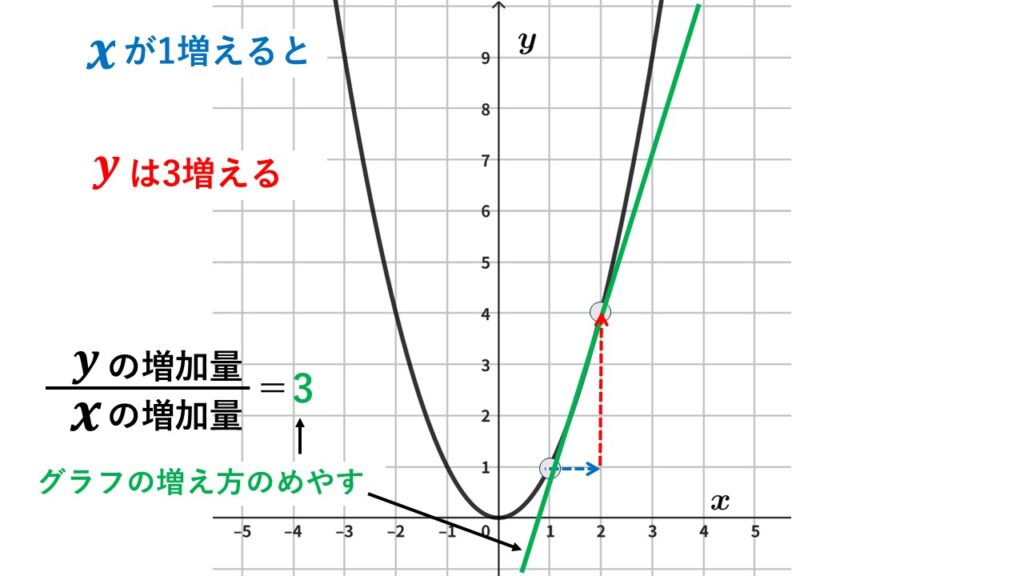
$x$が$1$から$2$まで$1$増えたときの変化の割合は$3$
増加していることがわかり、なおかつやや緩やかな増え方だとわかります。
$x$が$2$から$3$まで$1$増えたときの変化の割合は$5$
この区間では急激な増え方だとわかります。

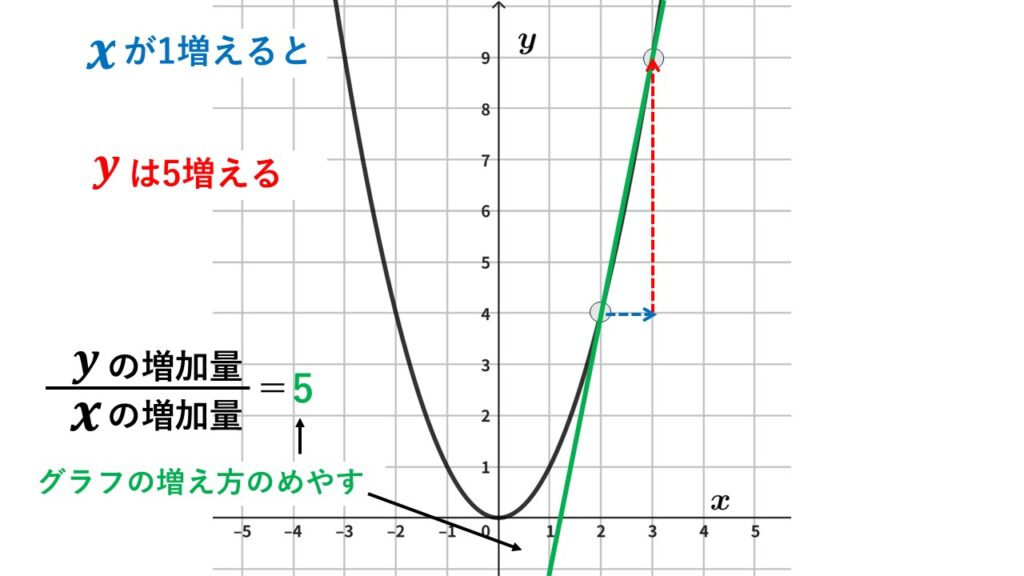
$y=ax^2$のグラフの変化の割合

1. $y=ax^2$のグラフの変化の割合は$x$の区間によって変化する
2. $y=ax^2$のグラフでは変化の割合を$a$としてはいけない
3. 変化の割合が正の値ならその$x$の区間では増加している
   変化の割合が負の値ならその$x$の区間では減少している
4. 変化の割合の絶対値が大きいと変化の仕方も大きくなっている

$x$の区間を広げたときの変化の割合

ここまでは$x$が1増加したときの変化の割合を考えました。
でも$x$の増加量が2や3というように、別の値で考えるときもあります。
ということで引き続き$y=x^2$を使って、$x$の増加量が1以外の場合で変化の割合を考えてみます。

$x$が$-3$から$0$まで$3$増えたときの変化の割合

$x$の増加量は$0-(-3)$より$3$
$y$の増加量は$0-9$より$-9$
変化の割合は$-3$です。

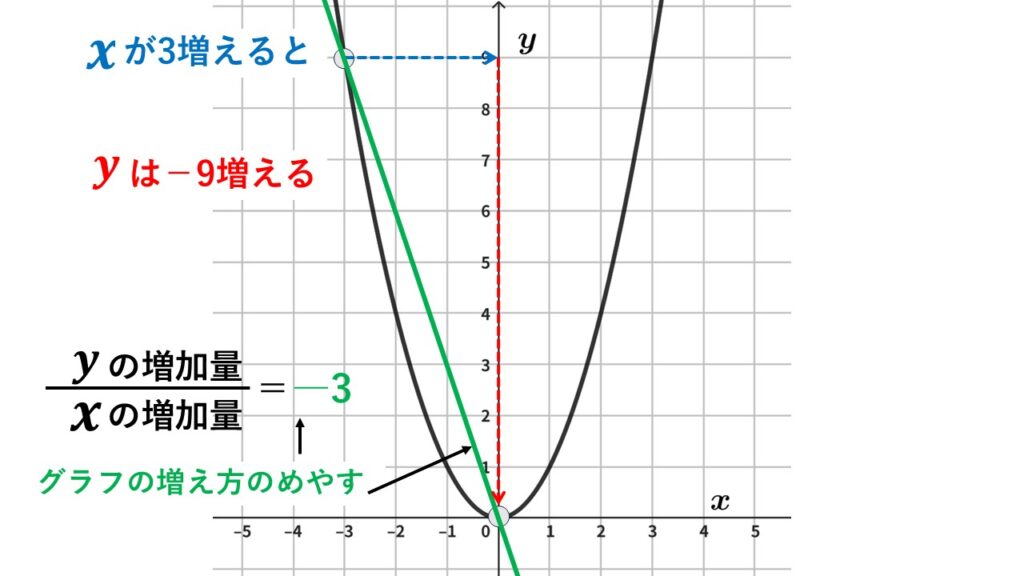
ここで1つ理解を深めてください。
変化の割合とは「$x$が1増えたときに$y$はいくつ増えるか」で「グラフの増え方の目安」と冒頭に書きました。
$-3\leqq x\leqq0$の範囲で考えたときの変化の割合が$-3$
これを別の言い方にすると

$-3\leqq x\leqq0$の範囲で考えたら$y$は$-9$増えるけど、
この範囲で$x$が1増えるとみなすと$y$は$-3$増えたことになってる

ということになります。ということはつまり

$-3\leqq x\leqq0$の範囲での平均の$y$の増え方は$-3$

と考えることができます。
もう少し例を見ていきます。

$x$が$-2$から$0$まで$2$増えたときの変化の割合

$x$の増加量は$0-(-2)$より$2$
$y$の増加量は$0-4$より$-4$
変化の割合は$-2$です。

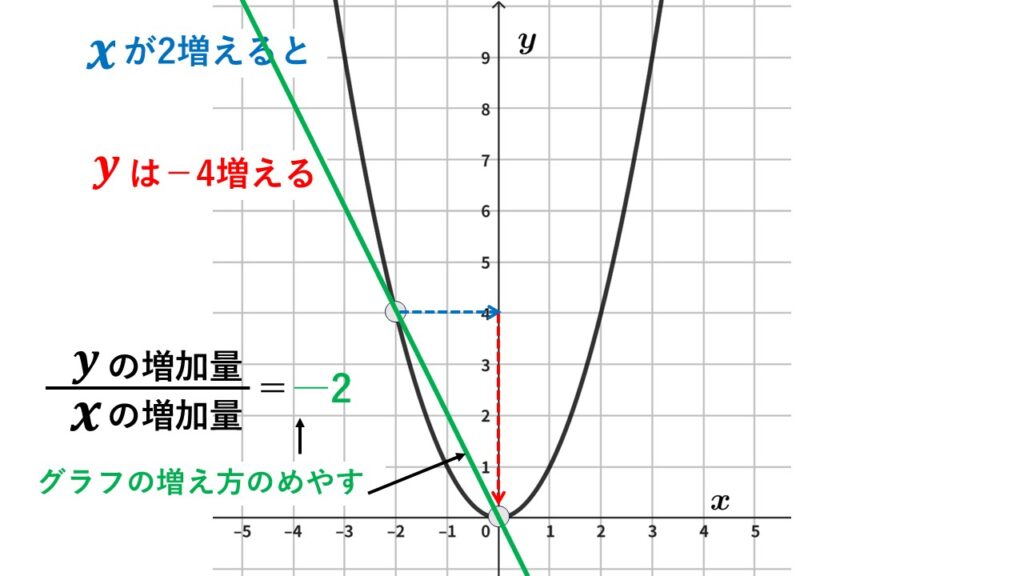
$-2\leqq x\leqq0$の範囲での$y$の増え方は$-4$だけど、
この区間での平均的な$y$の増え方は、
$x$が$1$増えるごとに$y$は$-2$増えている

ということですからね。

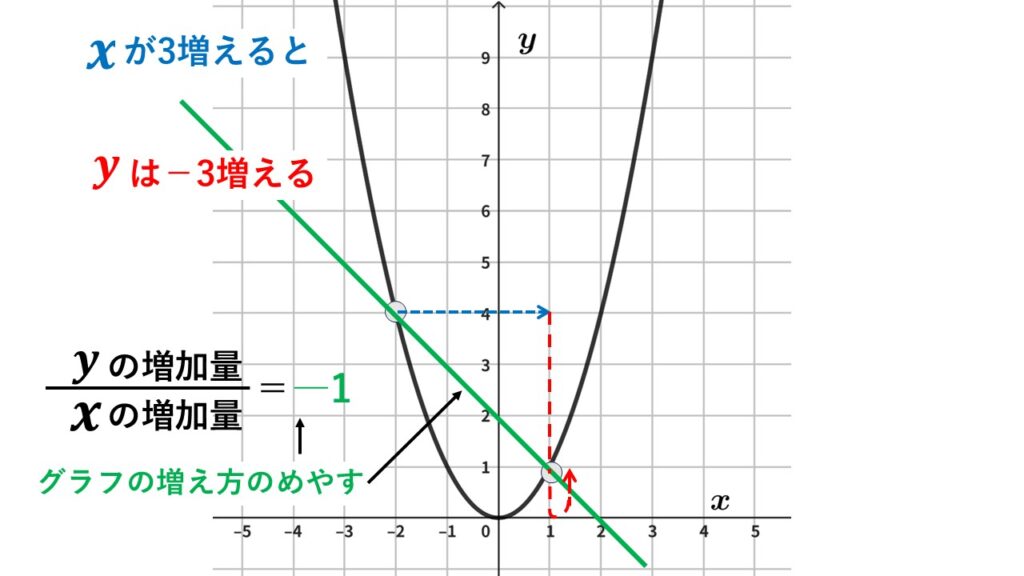
$x$が$-2$から$1$まで$3$増えたときの変化の割合

$x$の増加量は$1-(-2)$より$3$
$y$の増加量は$1-4$より$-3$
変化の割合は$-1$です。

$y$の増加量に注意!!
$y$は$4$から減り続けいったん$0$になります。
でもそこから折り返して最終的に$+1$となりました。
ということで$-2\leqq x\leqq1$における$y$の増加量は$-3$となります。

するとこの区間での平均的な$y$の増え方は
$x$が$1$増えるごとに$y$は$-1$増えている
ということになります。

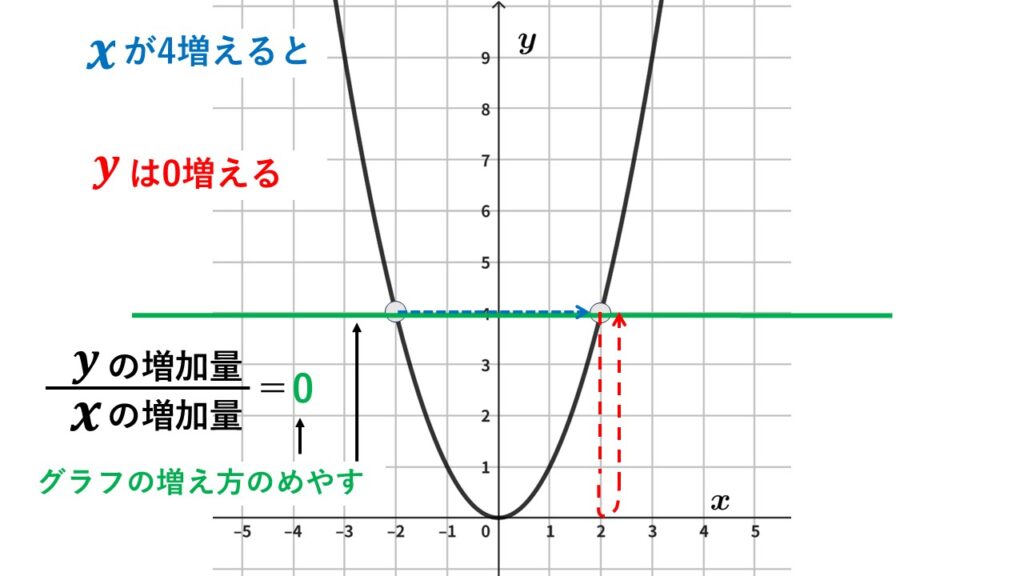
$x$が$-2$から$2$まで$4$増えたときの変化の割合

$x$の増加量は$2-(-2)$より$4$
$y$の増加量は$4-4$より$0$
変化の割合は$0$です。

$y$は$4$から減り続け、$x=0$のときにいったん$y=0$になりますが、そこから折り返して最終的に$+4$となりました。よって変化の割合は$0$。
$x$を細かく区切れば$y$は増減しますが、この区間を平均してみると$y$は変化していないと解釈できます。

$x$が$-2$から$3$まで$5$増えたときの変化の割合

$x$の増加量は$3-(-2)$より$5$
$y$の増加量は$9-4$より$5$
変化の割合は$1$です。

$y$は$4$から減り続け、$x=0$のときにいったん$y=0$になりますが、そこから折り返して最終的に$+5$となりました。そして変化の割合は$+1$。

つまりこの区間を平均してみると$y$は増えていると解釈できます。

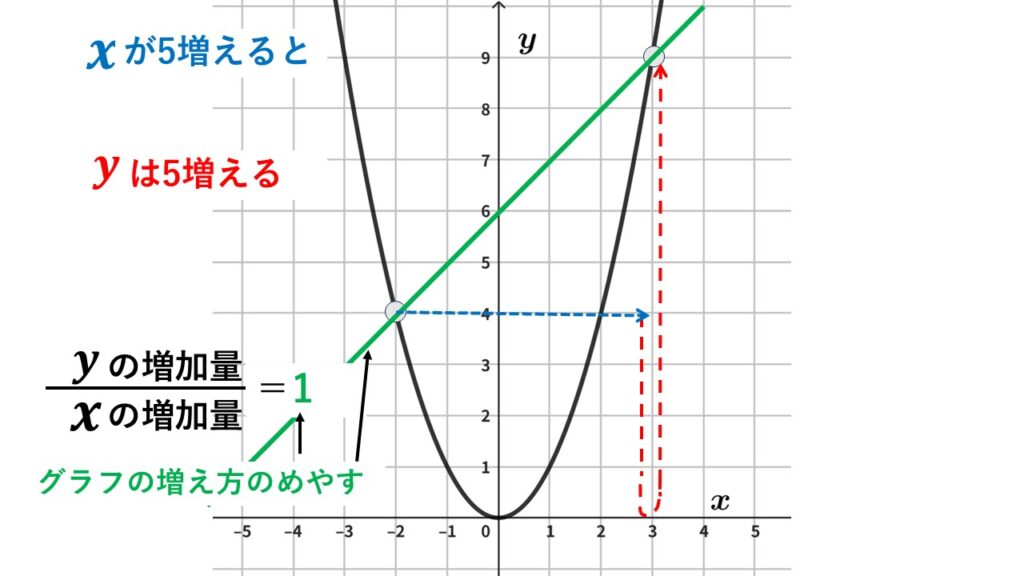
$x$の範囲を広げて考えたときの変化の割合は、$y$の平均の増え方を表している

ずいぶん長くなりましたが、ここまでとても重要なことがいくつも出てきました。
いったんここまでの内容をまとめておきます。

ここまでのまとめと基本例題

$y=ax^2$のグラフの変化の割合の意味

• $変化の割合=\dfrac{yの増加量}{xの増加量}$で計算する
• $y=ax^2$の$a$が変化の割合ということではない
• 変化の割合はグラフの増え方の目安となる
• $x$の区間によって変化の割合が変わる
• $x$の区間における平均の増え方を示している
• 変化の割合が$0$とは、その$x$の区間において$y$の増減が$0$と解釈できる
• 変化の割合は直線の傾きとして表せる

主なところは以上です。
これらは暗記するのではなく、問題を解きながら理解していくようにしましょう。
ということで変化の割合を求め方を基本例題でしっかり確認しましょう。

基本例題1
関数$y=2x^2$について、$x$の値が次のように変化するときの変化の割合を求めよ。
$(1)\:$$-2$から$-1$まで
$(2)\:$$1$から$4$まで
$(3)\:$$-2$から$1$まで

基本例題2
関数$y=-x^2$について、$x$の値が次のように変化するときの変化の割合を求めよ。
$(1)\:$$-2$から$-1$まで
$(2)\:$$1$から$4$まで
$(3)\:$$-2$から$1$まで

考え方
$変化の割合=\dfrac{yの増加量}{xの増加量}$を計算します。
$x$の増加量は$x$の変化後の値から変化前の値を引けば求まります。
$y$の変化量も同様に変化後の値から変化前の値を引きます。
慣れるまではグラフをかいて考えても良いですが、最終的には計算だけで求められるようにしましょう。

基本例題1　解答
$(1)\:x$の増加量は$(-1)-(-2)$より$1$
$\quad y$の増加量は$2-8$より$-6$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-6}{1}=-6$

$(2)\:x$の増加量は$4-1$より$3$
$\quad y$の増加量は$32-2$より$30$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{30}{3}=10$

$(3)\:x$の増加量は$1-(-2)$より$3$
$\quad y$の増加量は$2-8$より$-6$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-6}{3}=-2$

基本例題2　解答
$(1)\:x$の増加量は$(-1)-(-2)$より$1$
$\quad y$の増加量は$-(-1)^2-\{-(-2)^2\}=-1+4$より$3$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{3}{1}=3$

$(2)\:x$の増加量は$4-1$より$3$
$\quad y$の増加量は$-4^2-(-1^2)=-16+1$より$-15$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{-15}{3}=-5$

$(3)\:x$の増加量は$1-(-2)$より$3$
$\quad y$の増加量は$-1^2-\{-(-2)^2\}=-1+4$より$3$
$\quad 変化の割合=\dfrac{yの増加量}{xの増加量}=\dfrac{3}{3}=1$

ここまで変化の割合の計算お疲れ様です。ぶっちゃけ面倒だったと思います。
ところで基本例題合計6問。全て解き終わるまでにどの位時間がかかりましたか？
ある程度計算に慣れている人でもたぶん1～2分はかかったと思います。
計算を苦手にしている人はおそらく1分位でペン回しを始めたかもしれません。

でも、10秒程度でこれら6問全てを解答できるとしたら・・・。

そんな方法あるのか!?　と気になりますよね？
それがあるんです!!
1問につき1秒ちょっとで解答できる方法があるんです!!

学校ではあんまり教えてくれない、でも知っておくとものすげ～横着できる裏技。
このページの最後に、$y=ax^2$の変化の割合を一瞬で求めてしまう方法を紹介します。
これを覚えたらペン回しする暇さえなくなります。

$y=ax^2$の変化の割合を一瞬で求める裏技

$y=ax^2$の変化の割合を求めるときは、問題文に必ず$x$が変化する範囲が書かれています。
それと$a$の値を使って一瞬で求めます。

基本例題3
関数$y=5x^2$について、$x$の値が$1$から$3$まで変化するときの変化の割合を求めよ。

考え方

1. $x$の値が変化する始まりの値と終わりの値を足し算する
2. 足し算した結果に$x^2$の係数をかけ算する

この手順で解きます。

解答
$1+3=4\:$より$\:5\times4=20$
変化の割合は$20$

補足
基本例題1、2も裏技を使えば一瞬です。改めて確認してみてください。

これまで散々　$変化の割合=\dfrac{yの増加量}{xの増加量}$　で求めることを強調してきました。
強調してきたので当然これは重要な考え方で、この方法で解けるようにするのは必須です。

ただ早く求める方法があるならそれを使って解いた方が断然お得です。
ということでテストでこのような問題が出たら、裏技を使って解くようにしましょう。
明らかに簡単だし、計算ミスの危険も格段に下がります。早く解き終わった分、存分にペン回しもできると思います。

ただ$変化の割合=\dfrac{yの増加量}{xの増加量}$　で求めることを理解したうえで裏技を使うように!!

$y=ax^2$の変化の割合を一瞬で求める裏技

1. $x$の値が変化する始まりの値と終わりの値を足し算する
2. 足し算した結果に$x^2$の係数をかけ算する

なぜ裏技を使えるのか

なぜ一瞬で求まる裏技を使えるのかというと、変化の割合を求める式で説明できます。
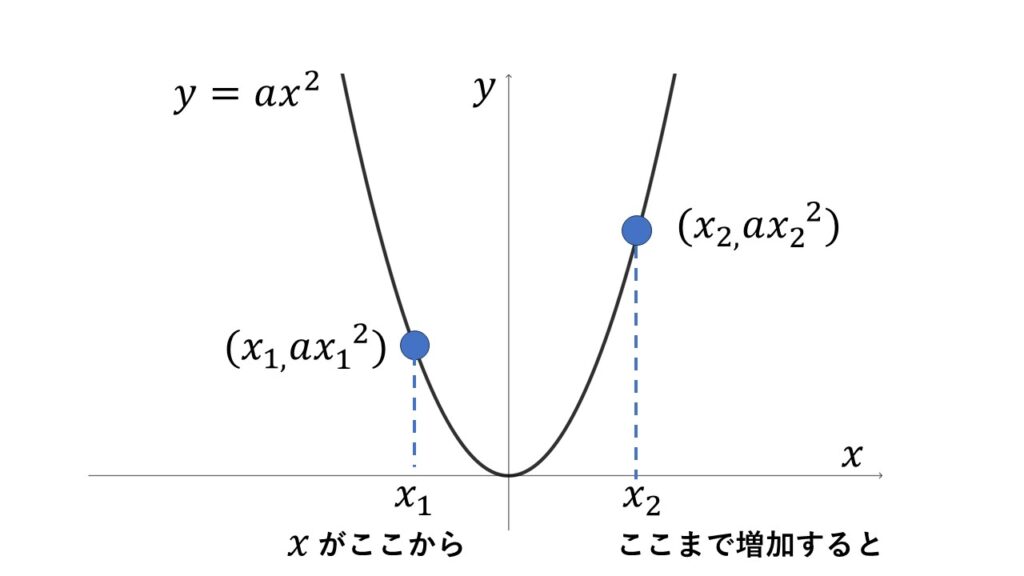
関数$\:y=ax^2\:$について、$x$が$x_{1}$から$x_{2}$まで増加したときの変化の割合を考えます。

※　具体的な数値で説明するとそのときの値だけの説明になってしまうので、$x_{1}$から$x_{2}$として説明します。
文字だらけの式になってしまいますが、この表記にも慣れてください。

$x_{1}$のとき$y$の値は$a{x_{1}}^2$
$x_{2}$のとき$y$の値は$a{x_{2}}^2$

よって
$x$の増加量は$x_2-x_1$
$y$の増加量は$a{x_2}^2-a{x_{1}}^2$

これより変化の割合は
$\begin{align}&\dfrac{a{x_{2}}^2-a{x_{1}}^2}{x_2-x_1}=\dfrac{a({x_{2}}^2-{x_{1}}^2)}{x_2-x_1}\\\\=&\dfrac{a(x_{2}+x_{1})(x_{2}-x_{1})}{x_2-x_1}\\\\=&a(x_2+x_1)\end{align}$

結果として
$x$の値が変化する始まりの値$(x_1)$と終わりの値$(x_2)$を足し、それに$a$をかけていることになりますね。

とても重要な内容なので念を押しておきますが、
変化の割合を求める式はしっかり理解し、そのうえで裏技を使うようにしましょう。