中学3年間の数学で最も重要度の高いものが$y=ax^2$のグラフです。
高校入試に直結する内容で、$y=ax^2$のグラフをかけるようにするために中1から数学を学んできた、といっても過言ではありません。
そのため$y=ax^2$のグラフは基礎の基礎からじっくり理解することが大切です。
ということでこのページでは、グラフのかき方とその特徴を詳しく解説していきます。
$y=ax^2$のグラフのかき方
まずはグラフのかき方を覚えてしまってください。
といっても、通る点を求めて線でつなぐだけなので特に難しいわけではありませんが・・・。
ただ、頂点$(0\:,\:0)$付近は特に丸みを持たせることに注意してください。
$y=ax^2$のグラフのかき方
- グラフが通る点を10か所くらい求める
- 求めた点をなめらかな曲線でつなぐ
グラフをかく手順としては上記の2点で、決して難しいものではありません。
ただグラフとして確認しておきたい点はたくさんあります。
では基本中の基本、$y=x^2$のグラフを上記の手順に沿ってかいてみましょう。
$y=x^2$のグラフ
①グラフが通る点を10か所くらい求める
実際に$y=x^2$の$x$に適当に数値を代入して、対応する$y$の値を求めます。
$x$が$0\leqq x\leqq9$の範囲では図のようになります。
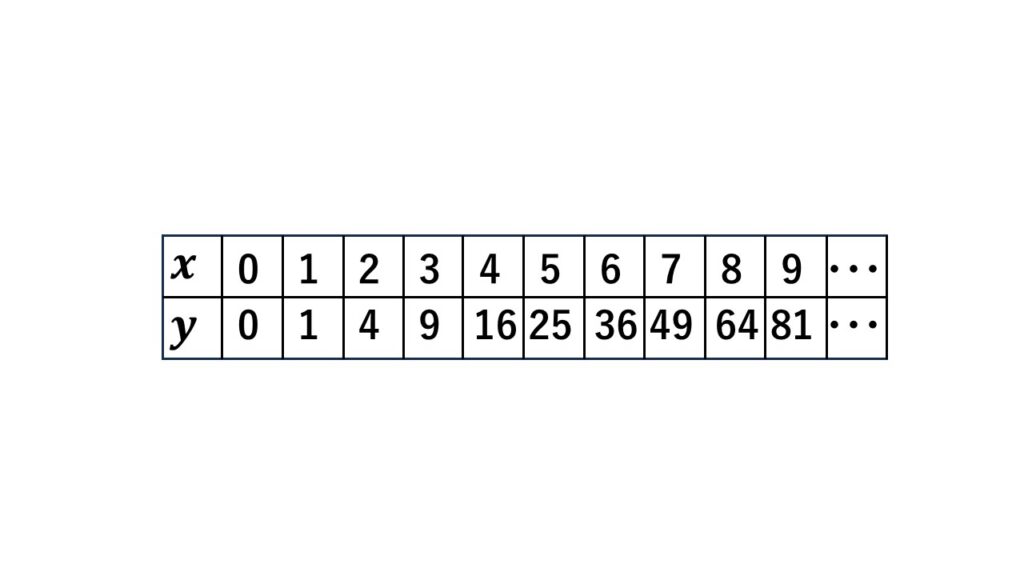
ここで1つ気づいてください。
計算上当然の結果なのですが、$x$の値が増えるにつれ、$y$の値の増え方が急激になっています。
ところで$x$の値は正だけでなく負の値も取ります。
$x$が$-9\leqq x\leqq0$の範囲では図のようになります。
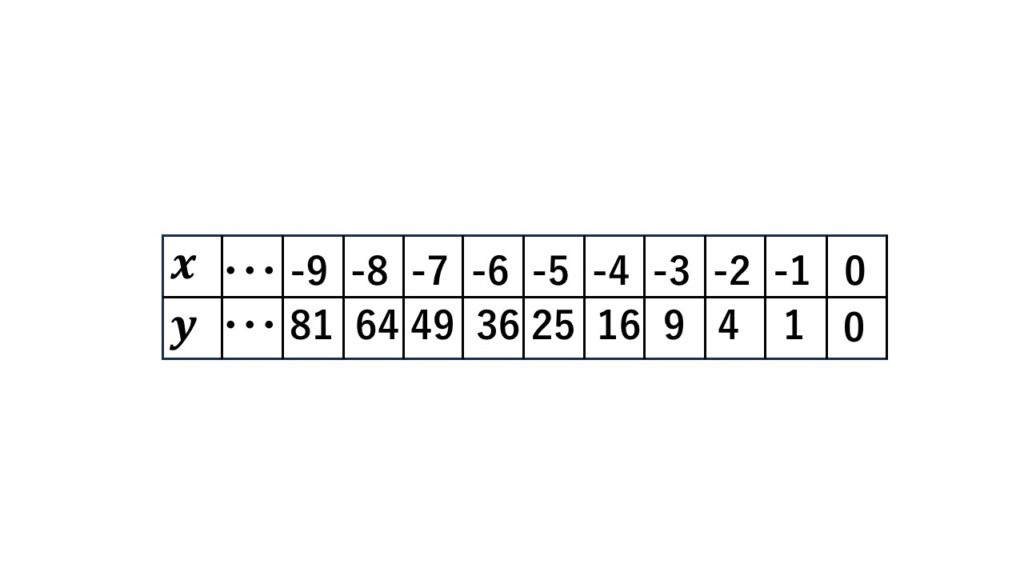
ここで1つ気づいてください。
計算上当然の結果なのですが、$x$が負の値でも$y$は正の値を取っています。
グラフが通る点はまだまだ無限にありますが、これでとりあえず$y=x^2$のグラフが通る点が求まりました。
②求めた点をなめらかな曲線でつなぐ
なめらなか曲線というところがポイント。
直線ではないのでフリーハンドで、できれば一筆書きにします。そのため、少しくらいいびつな形になってしまうのは仕方ありません。
グラフが通る点として上記では$-9\leqq x\leqq9$の範囲で通る点を求めましたが、実際はそこまで求める必要はなく、概形がわかる程度で求めれば十分です。
注意点
①なめらかな曲線になる。まっすぐな線にならないよう気をつけること。
②外側に膨らむようなグラフになる。内側に凹む形にしないこと。
③グラフの頂点はU字型。V字型には絶対にしないこと。
④変域などの条件がない限り、グラフは無限に続くようにかくこと。
ということでグラフはこのようになります。
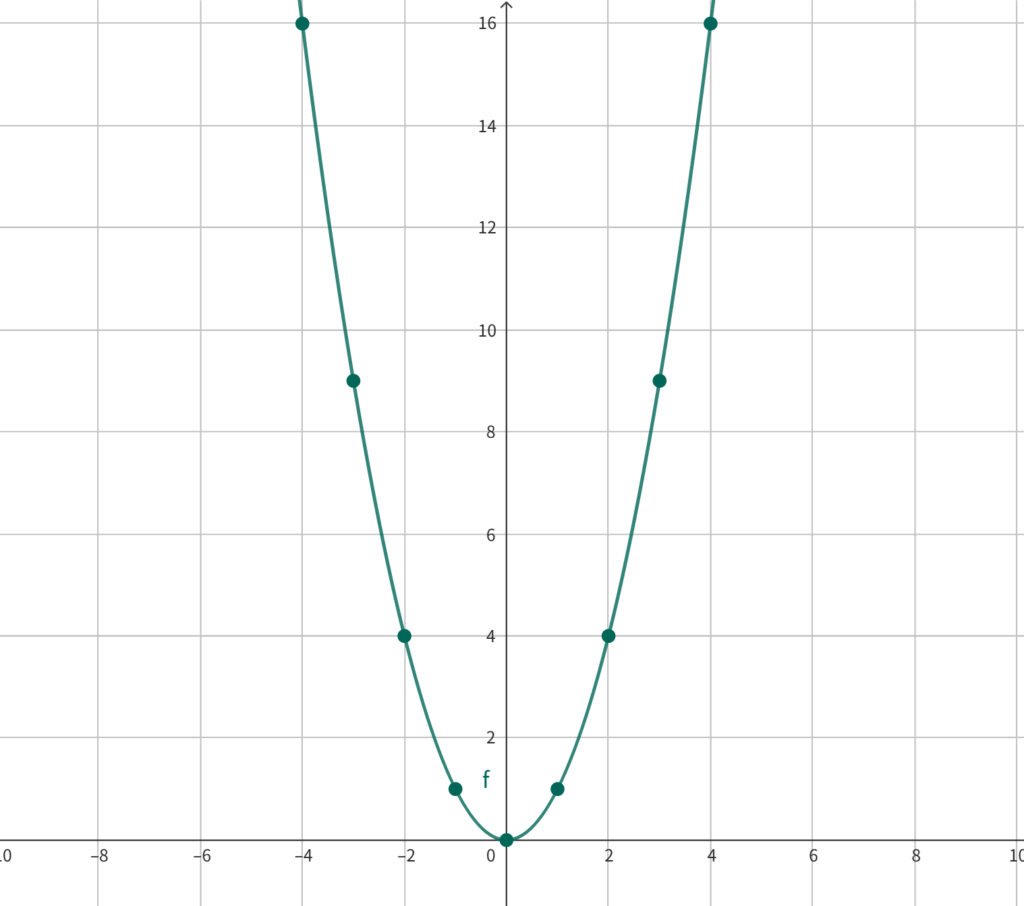
なぜ曲線なのか?
$y=ax^2$のグラフが外側に膨らむような曲線になることを証明するには、中学レベルの数学を大きく超える知識が必要になります。
そのため中学の段階では感覚的に覚えておけば良いです。
ではどうして曲線になるのか?
引き続き$y=x^2$で解説します。
$y=x^2$の通る点をより細かく小数の範囲で考えます。
$x$が負のときも考えますが、$2$乗より$y$は正の値なので表は割愛します。
通る点は表のようになります。
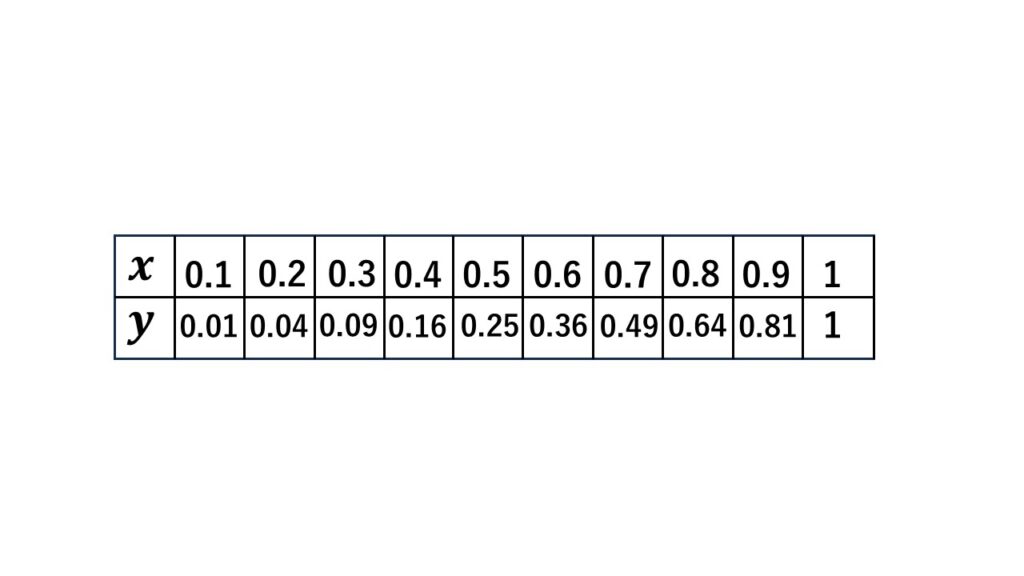
そして$-1\leqq x\leqq1$の範囲を拡大したものが次のグラフです。
青い曲線は$y=x^2$
比較するために赤で$y=x$を表しました。
中1で学んでいる通り、$y=x$は直線です。
$y=x^2$が通る点を結んでいくと直線にならないのがわかると思います。
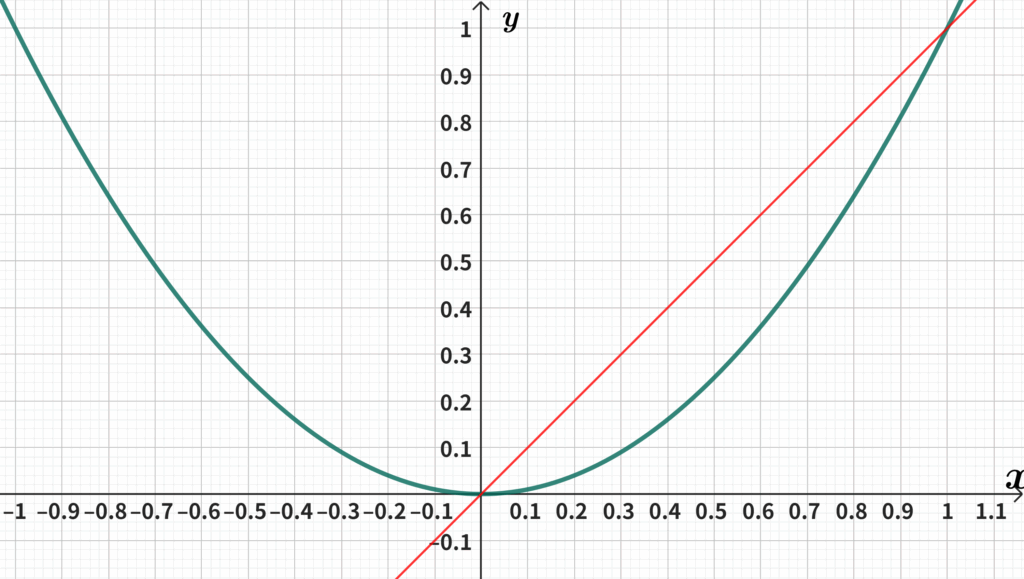
通る点を細かく見ていくと、外側に膨らむような形になっています。
さらに頂点も丸みを帯びたU字型で、V字の様にとがっていません。
ここでは$x$を小数第1位までしか考えませんでしたが、さらに細かく考えていくと、よりはっきりと曲線になることがわかります。
ここは説明の都合上$-1\leqq x\leqq1$で解説しましたが、どの区間でも同様のことがいえます。
なお、実際の問題では特に指示がない限り、$x$は整数の範囲で考えれば十分です。
一筆書きにしないといけないのか?
繰り返しますが、$y=ax^2$のグラフは必ずフリーハンドでかきます。できれば一筆書きにします。
曲線のグラフなので定規を使った時点で曲線にならなくなり、別のグラフをかいたことになってしまいます。
そのためテストでは誤答扱いになります。
一筆書きはできればで構いません。
というより慣れない段階で一筆書きなど無理です。(慣れてても難しい)
ただ一筆書きとあえて書いたのは理由があります。
一筆書きにしないとグラフがいったん途切れる、つまり連続した線になりません。
このことが厄介。
連続した線でないと途中までは$y=ax^2$のグラフで、その先は別の関数のグラフが合わさったのもと解釈される危険が生じます。
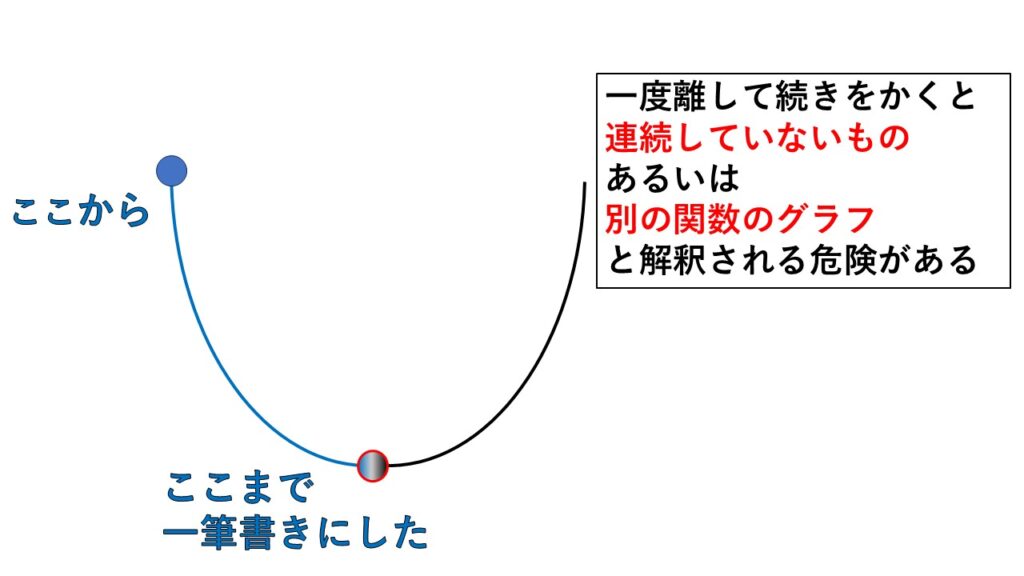
すると本来必要なものから大きく違ったことになってしまいます。
もっともこれは厳密な話なので、一筆書きについて気にしすぎる必要はありません。
ただ、いったん途切れた所から再度グラフをかくと、本来のグラフの形からどうしてもずれてしまいます。
そのずれがあまりにも大きくなるとやはりテストでは減点の対象となるので、そこは注意が必要です。
ここまでのまとめ
$y=ax^2$のグラフのかき方
・グラフが通る点を10か所くらい求める
・求めた点をなめらかな曲線で外側に膨らむようにつなぐ
・グラフの折り返し点(頂点)はU字型にする
・できれば一筆書きにする
ここまでのことをふまえ、$y=ax^2$のグラフをかく練習をしましょう。
基本例題1
次のグラフをかけ。
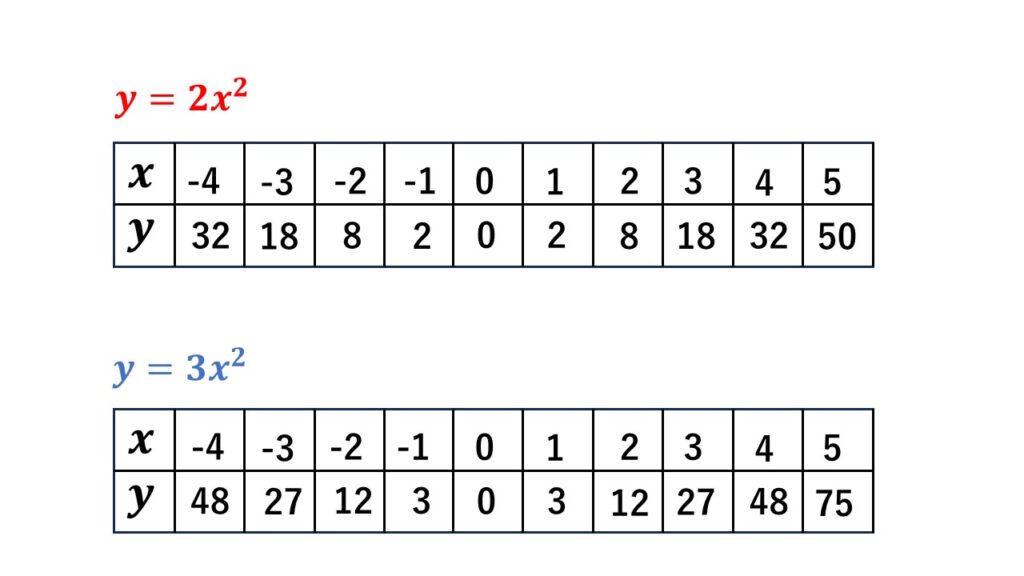
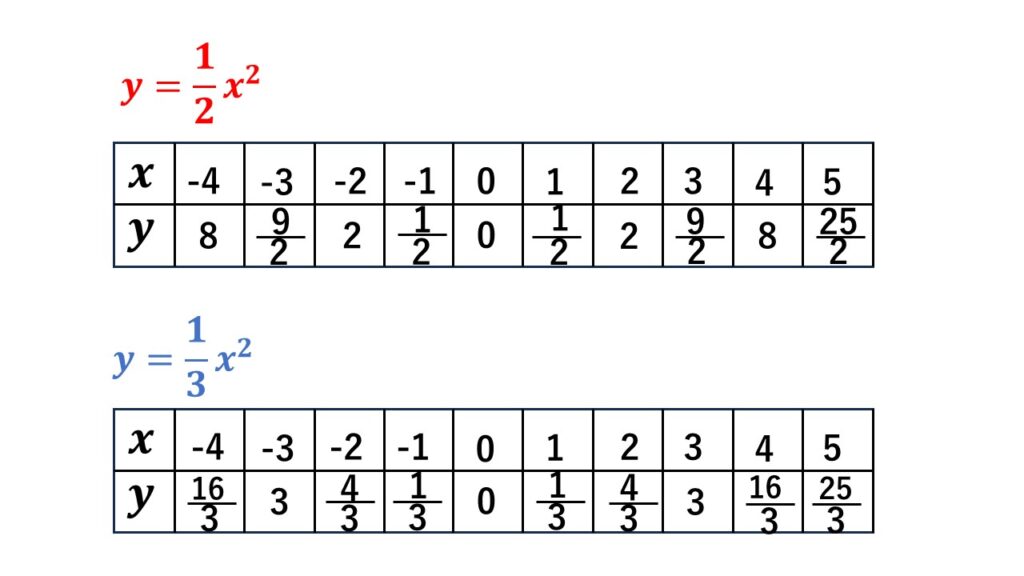
$\begin{align}(1)&\:y=2x^2&\quad&(2)\:y=3x^2\\
(3)&\:y=\dfrac{1}{2}x^2&\quad&(4)\:y=\dfrac{1}{3}x^2\end{align}$
解答
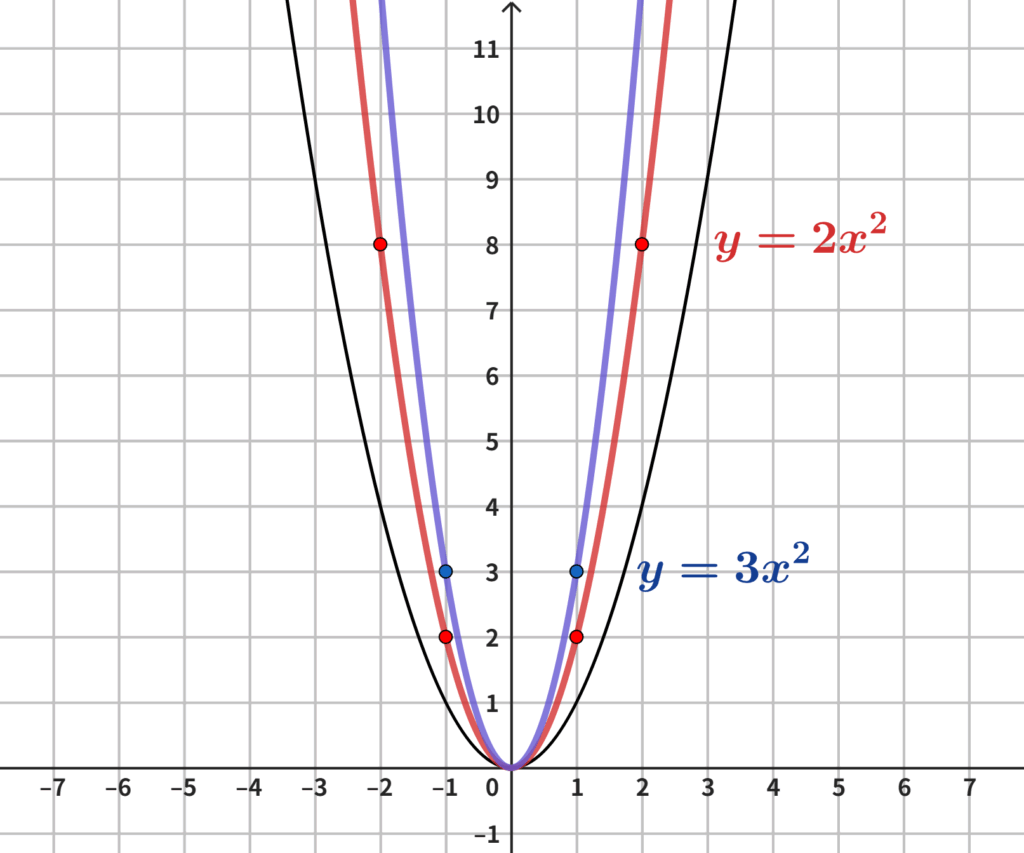
それぞれ以下のグラフとなります。
グラフが通る点を10か所位求めて、グラフのおおよその形を把握してかきます。
ただ目盛りの限界もあるので、$x$座標と$y$座標がともに整数の部分(格子点という)でグラフが通る点を明確にしてかきます。
通る点の表は解答にかく必要はありません。
なおここでは参考として、$y=x^2$のグラフを黒でかいてあります。
$y=ax^2$のグラフは$a$の値で特徴が決まる
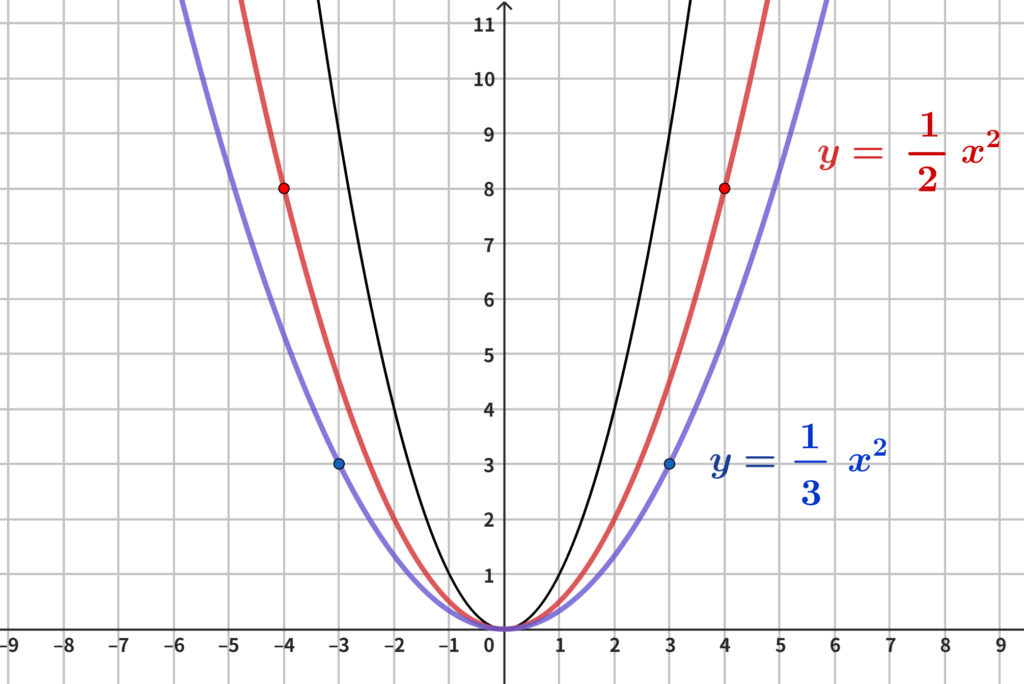
基本例題1では$y=x^2$も含め5つのグラフができました。
ここで$y=ax^2$のグラフの特徴をまとめます。
$y=ax^2$のグラフの特徴
- $a>0$ならば上に開いた形になる(下に凸となる)
- $a$の絶対値が$0$に近いほど大きく広がった形になる
- $a$の絶対値が大きいほど広がりが狭い
- 原点を通る(グラフの折り返し点なので原点が頂点となる)
- $y$軸について対称となる
改めて基本例題1のグラフで、$a$の値とグラフの形状を関連させてよ~~~~く見てください。
$a$の値が$3$よりも$2$、$2$よりの$1$、$1$よりも分数という様に、絶対値が$0$に近づくほどグラフの幅が広くなっています。
また$y$軸を対称の軸とした線対称になっています。
ということは、グラフが通る点を求める際$x$が正の範囲を求めれば、$x$が負の範囲は計算しなくてもわかりますよね。
これらの特徴はグラフをかきながら理解するようにしましょう。
ところで$a<0$のときは下に開いたグラフになります(上に凸となる)。
上記特徴をふまえもう少しグラフをかいてみましょう。
基本例題2
次のグラフをかけ。
$\begin{align}(1)&\:y=-x^2&\quad&(2)\:y=-2x^2\\
(3)&\:y=-\dfrac{1}{2}x^2&\quad&(4)\:y=-\dfrac{1}{4}x^2\end{align}$
解答
全て$a<0$なので下に開いたグラフ(上に凸)になります。
$a<0$でも$y=ax^2$のグラフの特徴がみられることを確認してください。
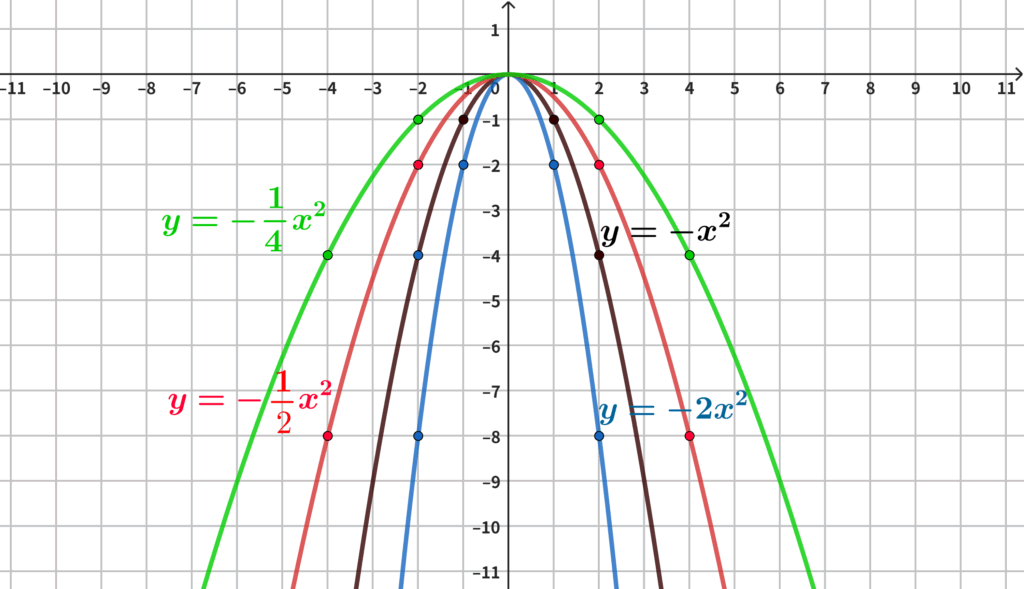
$a$の絶対値が$0$に近いほど大きく広がった形になる。
ということは言い方を変えると、
$a$の絶対値が$0$に近いほど緩やかなグラフの増減になる
とも言えます。
合わせて理解しておきましょう。
それではこのページのまとめとして練習問題にチャレンジしましょう。
$y=ax^2$のグラフの特徴を使った練習問題
練習問題
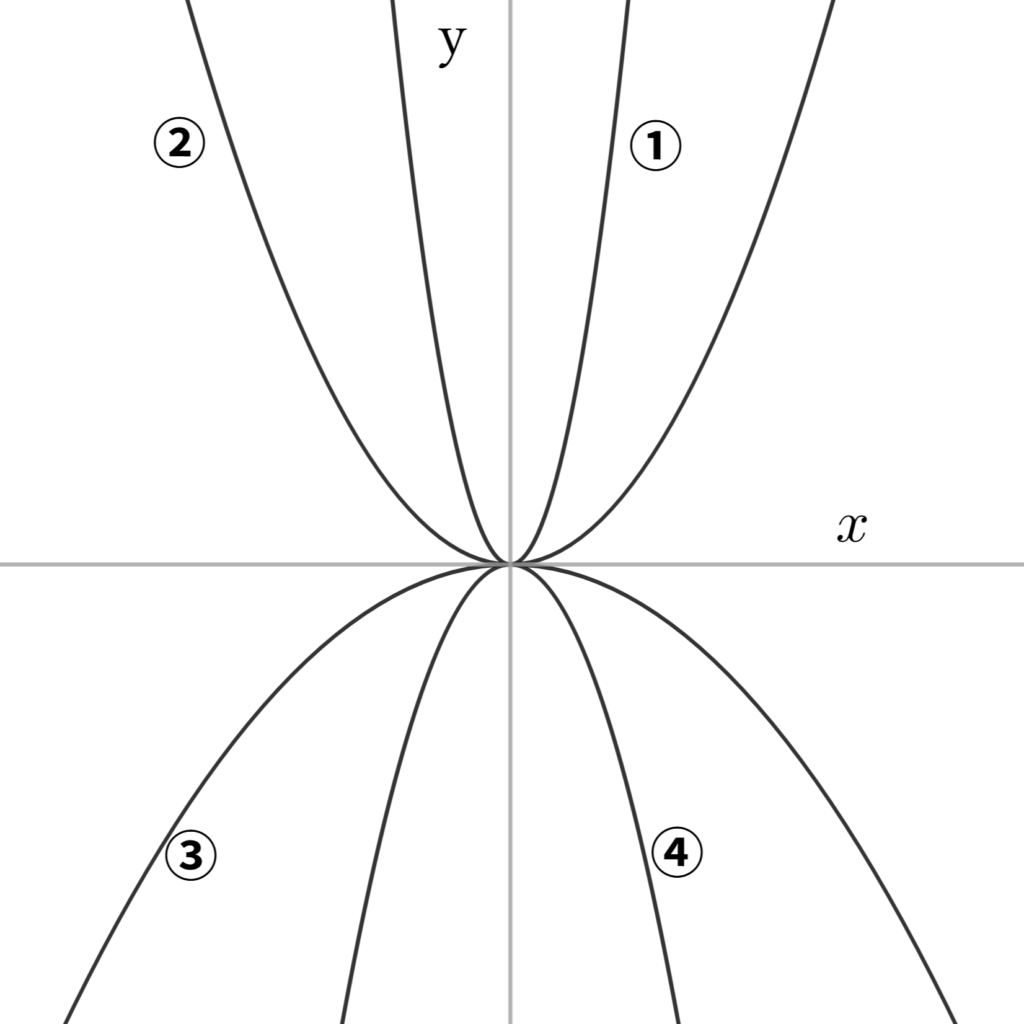
$(1)\:$次の放物線のグラフ①~④は、
関数
$\begin{align}&y=\dfrac{2}{3}x^2&\quad y=&-2x^2\\
&y=-\dfrac{2}{7}x^2&\quad y=&5x^2\end{align}$
のいずれかである。
①~④にあてはまる関数を選べ。
$(2)\:$③の放物線と$x$軸について対称な放物線の式を答えよ。
考え方
$a$が正か負か、また$a$の絶対値の大きさとグラフの形状を関連させていきます。
座標に目盛りが無くても答えられるようにしましょう。
解答
$(1)\:①\:y=5x^2\quad②\:y=\dfrac{2}{3}x^2\quad③\:y=-\dfrac{2}{7}x^2\quad④\:y=-2x^2$
$(2)\:y=\dfrac{2}{7}x^2$
