放物線のグラフと直線のグラフがつくる図形

放物線$y=ax^2$と直線$y=Ax+B$がつくる図形問題では、放物線と直線の交点を求めることが必須です。
交点を求めるためには、$y=ax^2$と$y=Ax+B$を連立方程式にして解きます。
そして求めた交点をもとに辺の長さを導きます。
交点が求まれば問題の半分が解けたも同然。後は問題の条件に沿って考えていきます。

なお、交点の座標の求め方について不安がある人は、こちらのページで復習してください。
本ページは交点の座標の求め方は既に理解していることとして解説していきます。

$x$座標に文字を代入して距離を表す

本題に入る前に基本事項の確認。

「$x$座標を$\:s\:$とおくと・・・」

というように、関数と図形の融合問題を苦手とする人は、文字を使った座標の表し方で混乱してしまうことが多いようです。
次の例題で、まず文字を使った座標の表し方に慣れておきましょう。

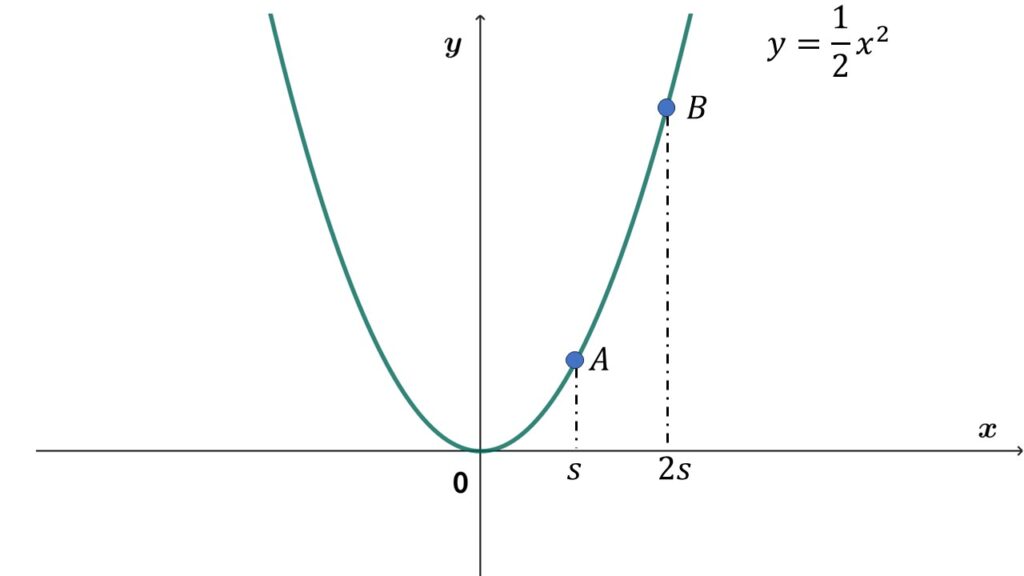
超基本例題1


関数$\:y=\dfrac{1}{2}x^2$上の点$A$の$x$座標が$s$、点$B$の$x$座標が$2s$のとき、点$A,B$の座標を$\:s\:$を使って表せ。

考え方
$y=\dfrac{1}{2}x^2\:$の$\:x\:$に、通る点の$x$座標を代入して$y$座標を求めます。
文字に文字を代入する形になります。

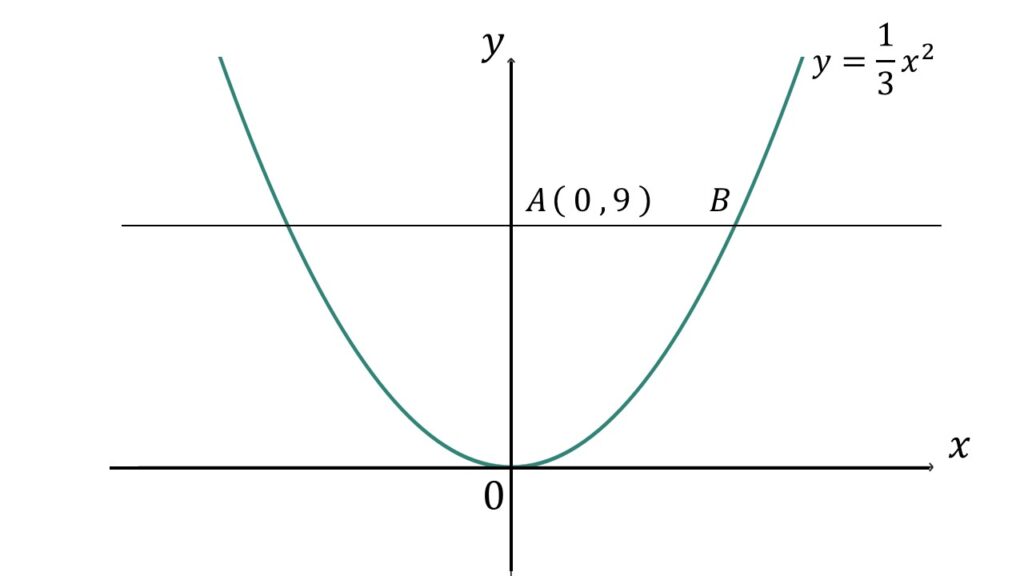
超基本例題2


$(1)\quad$図のように、点$A(0\:,\:9)$を通る$x$軸に平行な直線と、
放物線$\:y=\dfrac{1}{3}x^2$との交点を$B$とする。
このときの点$B$の座標を求めよ。なお$B$の$x$座標は正の値とする。

$(2)\quad$$AB$の長さを表せ。

考え方
$(1)\quad$$x$軸に平行な直線とあるので$B$の$y$座標は$9$とわかります。
よって$\:y=\dfrac{1}{3}x^2$に$y=9$を代入して$x$を求めます。
$(2)\quad$$AB$の長さ、つまり横の長さを求めるので$x$座標に注目します。

解答
$\begin{align}(1)\:9&=\dfrac{1}{3}x^2\\\\27&=x^2\\x&=\pm 3\sqrt3\end{align}$
$\quad B$の$x$座標は正より$x=3\sqrt3$
　よって$\quad B(3\sqrt3\:,\:9)$

$(2)\:A(0\:,\:9)\;, B(3\sqrt3\:,\:9)$より
$\quad AB=3\sqrt3-0=3\sqrt3$

解説
点の座標を求めるために与えられた$y$座標をもとに$x$座標を導く。
この考え方自体は中1のときからやっています。

横の長さを求めるときは$x$座標
縦の長さを求めるときは$y$座標
に注目します。

座標を求めた上で距離を求める。
関数と図形の融合問題ではパターン化された出題方法です。

次に超基本例題1、2の考え方を踏まえ、文字を使った長さの表し方を確認します。

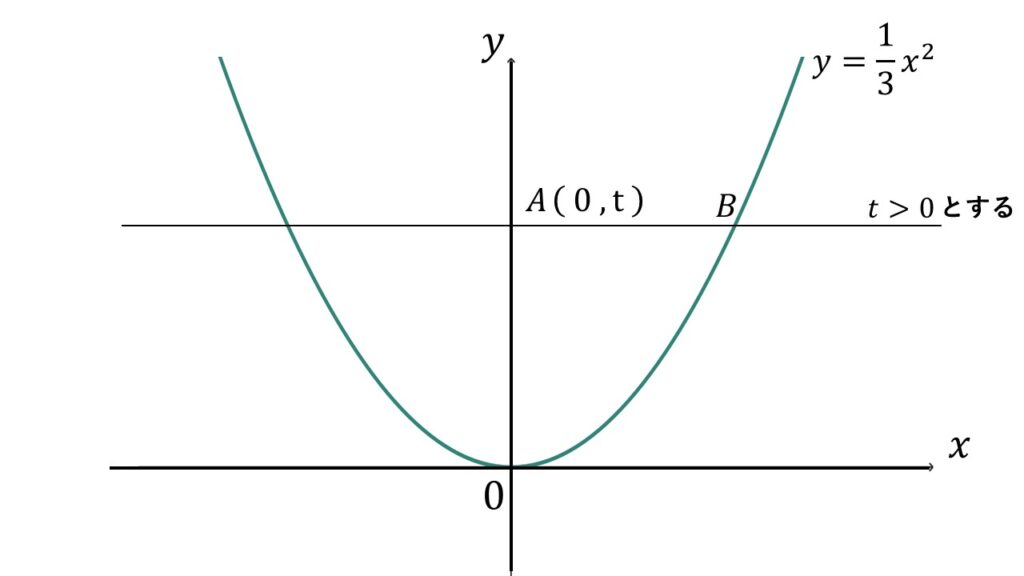
超基本例題3

$(1)\quad$図のように、点$A(0\:,\:t)$を通る$x$軸に平行な直線と、放物線$\:y=\dfrac{1}{3}x^2$との交点を$B$とする。
このときの点$B$の座標を求めよ。
なお$\:t>0$、$B$の$x$座標は正の値とする。

$(2)\quad$$AB$の長さを$t$を使って表せ。

考え方
超基本例題2と同じです。
数値ではなく$t$を代入するので文字ばっかりの結果になります。

解説
座標を求めるのに、その結果が文字ばっかりの形として答えになる。
関数の問題ではこの様なことはよくあります。
というより、
関数の問題を解く過程でいったん座標を文字で表す
ということを数学ではよく使います。

文字ばっかりの座標を見るとどこか間違えてるんじゃないかと不安になりますが、練習を重ねて慣れるようにしておきましょう。

本ページの本題を解くための準備をして、超基本例題で必要な知識を身につけました。

ここからが本題。以下は高校入試に直結する考え方を含む超重要な応用問題です。
ただ応用問題といっても、必要な考え方は上記で学んでいます。
解き方に慣れるのはもちろんのこと、出題パターンも押さえておきましょう。

放物線と直線がつくる図形

座標から放物線の式を求める

基本例題1

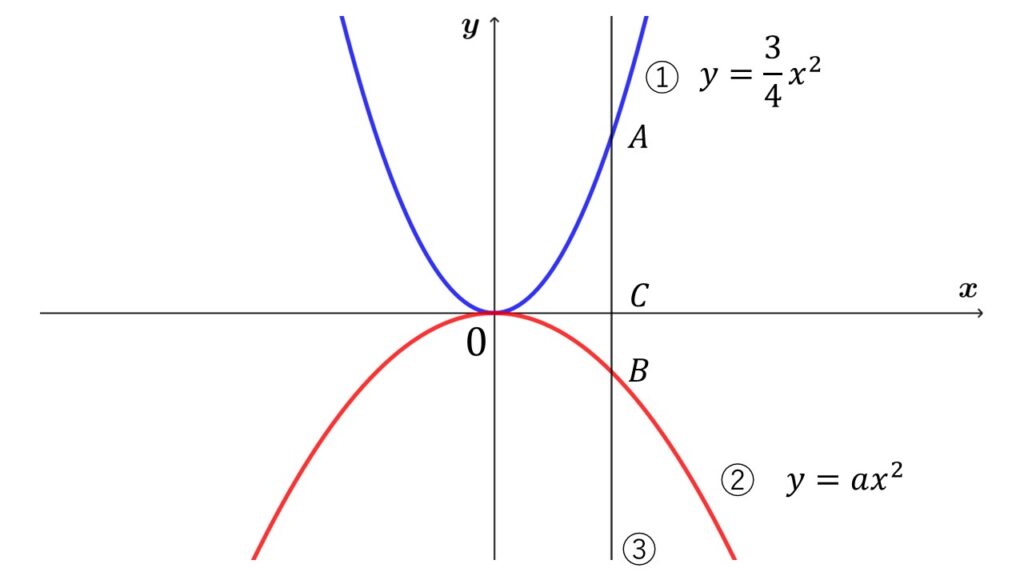
図の①は関数$y=\dfrac{3}{4}x^2$、②は関数$y=ax^2$である。また③は$y$軸に平行な直線で、①、②との交点をそれぞれ$A,B$とし、$x$軸との交点を$C$とする。
$AB=4$となるとき次の問いに答えよ。

$(1)\quad$$C$の$x$座標を$s$とするとき、点$A$、$点B$の座標を$s$を使って表せ。

$(2)\quad s=2$のとき②の式を求めよ。

考え方
$(1)\quad$③は$y$軸に平行とあるので、$A,B,C$の$x$座標は全て等しくなります。
問題文から$C$の$x$座標が$s$なので、①②の$x$に$s$を代入して求めます。

$(2)\quad$②の放物線の式を求めるには$a$の値を特定する必要があります。
そのためには$B$の座標がわからないと解けません。
そしてこの$B$の座標を求めるのがポイント。
その手がかりが$AB=4$です。もちろん$AB=4$とは$AB$の長さが$4$ということです。
ちなみに②のグラフは上に凸なので、この時点で$a<0$であることが特定できます。

入試直結の重要な問題なので、しばらく考えてから解答に進みましょう。

解答
$(1)\quad$③は$y$軸に平行な直線なので、点$A,B,C$の$x$座標はそれぞれ$s$となる。
　①、②の$x$にそれぞれ$s$を代入して
$\quad y=\dfrac{3}{4}x^2=\dfrac{3}{4}s^2\quad$

　よって$\quad A(s\:,\:\dfrac{3}{4}s^2)$

$\quad y=ax^2=as^2$
　よって$\quad B(s\:,\:as^2)$

　ここで$s=2$のときなので、
$\begin{align}\quad\dfrac{3}{4}\times2^2-a\times2^2&=4\\3-4a&=4\\-4a&=1\\a&=-\dfrac{1}{4}\end{align}$

　これより②の式は
$\quad y=-\dfrac{1}{4}x^2$

解説
$(1)$は$(2)$を解くための誘導問題になっています。
最終的には$(1)$が無くても自力で$(2)$の問題を解けるのが望ましいです。
ということで、解き方の流れをしっかり確認しておきましょう。

文字を使って座標を表すとき、$(s\:,\:t\:)$のように2種類の文字を使ってしまうと収拾がつかなくなります。
本問の場合、$x$に文字$s$を代入することで$y$座標も$s$で表すことができる、つまり1種類の文字で座標を表すことができます。そうすることで計算がスムーズに進むようになります。
$(1)$の問題を改めて見直して、座標の表し方を理解しましょう。

放物線と正方形

基本例題2

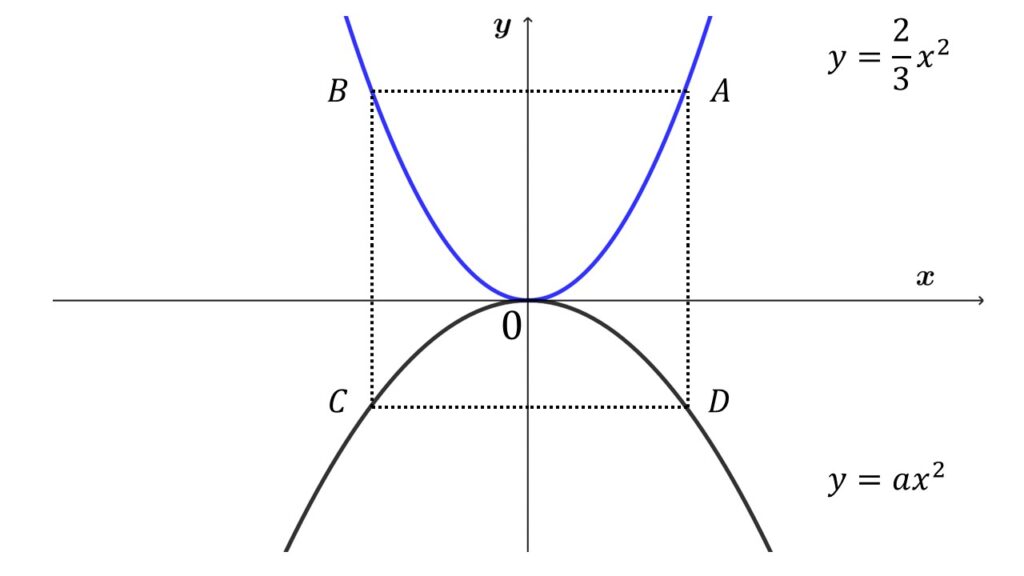
図で点$A,B$は関数$y=\dfrac{2}{3}x^2$のグラフ上の点で、点$C,D$は関数$y=ax^2$のグラフ上の点である。また、四角形$ABCD$は正方形で、辺$AB$は$x$軸に平行である。
点$A$の$x$座標が$2$のとき次の問いに答えよ。
$(1)\quad$点$A$の座標を求めよ。

$(2)\quad$辺$AD$の長さを求めよ。

$(3)\quad a$の値を求めよ。

考え方
$(1)\:$点$A$の$x$座標が$2$のときとあるので、$y=\dfrac{2}{3}x^2$の$x$に$2$を代入するだけです。
$(2)\:y=ax^2$のグラフは$y$軸を境に左右対称です。そのため$A$の座標がわかれば$B$の座標もわかります。すると$AB$の長さがわかります。あとは正方形は全ての辺の長さが等しいことに注目します。
$(3)\:$点$D$の座標を$y=ax^2\:$に代入して$a$を求めます。点$D$の座標は$(1),(2)$が求まればわかります。図から$a<0$となることに注意!!

解答
$(1)\:A$の$x$座標が$2$より
$\begin{align}\quad y&=\dfrac{2}{3}x^2\\\\&=\dfrac{2}{3}\times2^2=\dfrac{8}{3}\end{align}$
　
　よって$A(2\:,\:\dfrac{8}{3})$

$(2)\:A(2\:,\:\dfrac{8}{3})$より$\:B(-2\:,\:\dfrac{8}{3})$

　正方形の辺の長さは全て等しいので$AB=AD$
　したがって$\:AD=4$

$(3)\:AD＝4$より$D$の座標を求める

　これより$y=ax^2$に$D$の座標を代入して
$\begin{align}\quad -\dfrac{4}{3}&=a\times2^2\\\\-\dfrac{4}{3}&=4a\\\\-4&=12a\\\\a&=-\dfrac{1}{3}\end{align}$

解説
この問題の最終目標は$y=ax^2$の式を特定することです。
そのためには$y=ax^2$が通る点の座標がわからないと解けません。
そこで解法の手がかりとなるのが正方形の性質。
点$A$の座標をもとに横の長を求め、それを縦の長さに関連させて点$D$の座標を求めました。

$(1),(2)$は$y=ax^2$の式を特定するための誘導問題です。
高校入試までには誘導問題が無くても自力で$y=ax^2$を求められるようにしておきましょう。

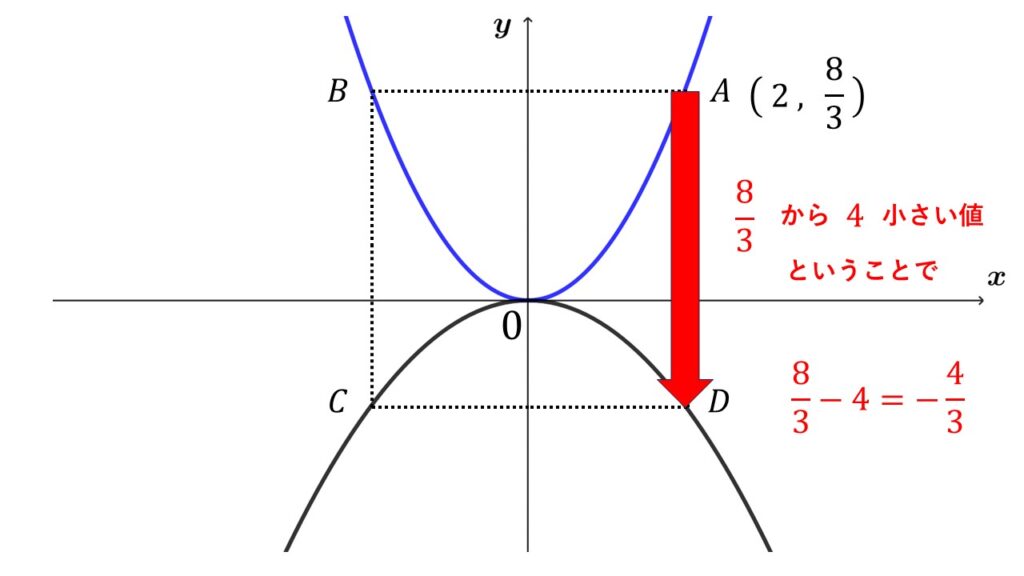
補足
上記解答は辺の長さに注目した解き方だったので
$4=y+\dfrac{8}{3}$
として計算しました。

ただ座標そのものに注目した場合、
$A$の$y$座標から$4$下がった点と考えて
$\begin{align}&\quad\dfrac{8}{3}-4\\\\&=\dfrac{8}{3}-\dfrac{12}{3}=-\dfrac{4}{3}\end{align}$
となります。
こちらの解き方の方が直接点$D$の$y$座標が求まるので符号ミスを防げます。

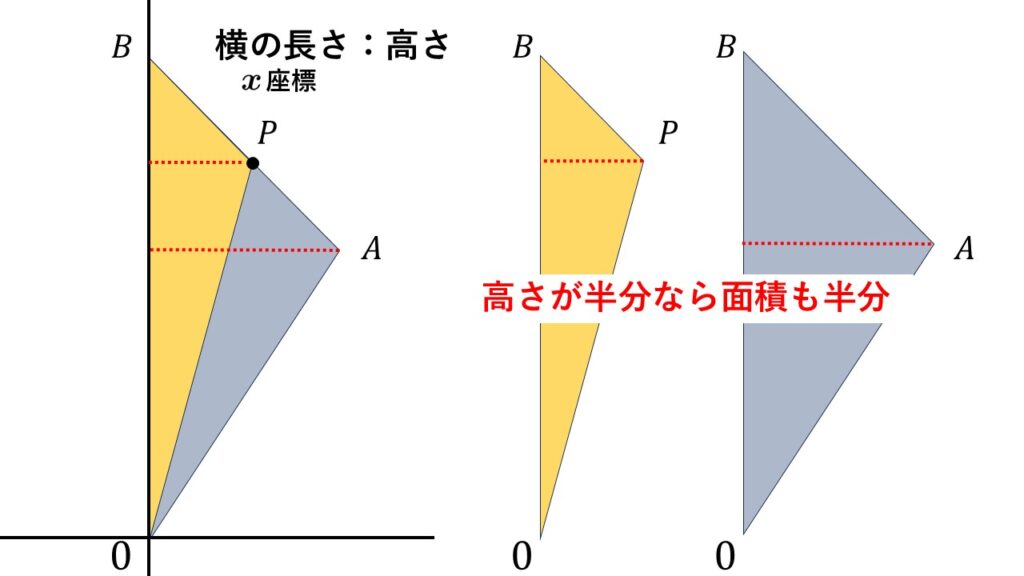
三角形の面積を半分にする点の座標

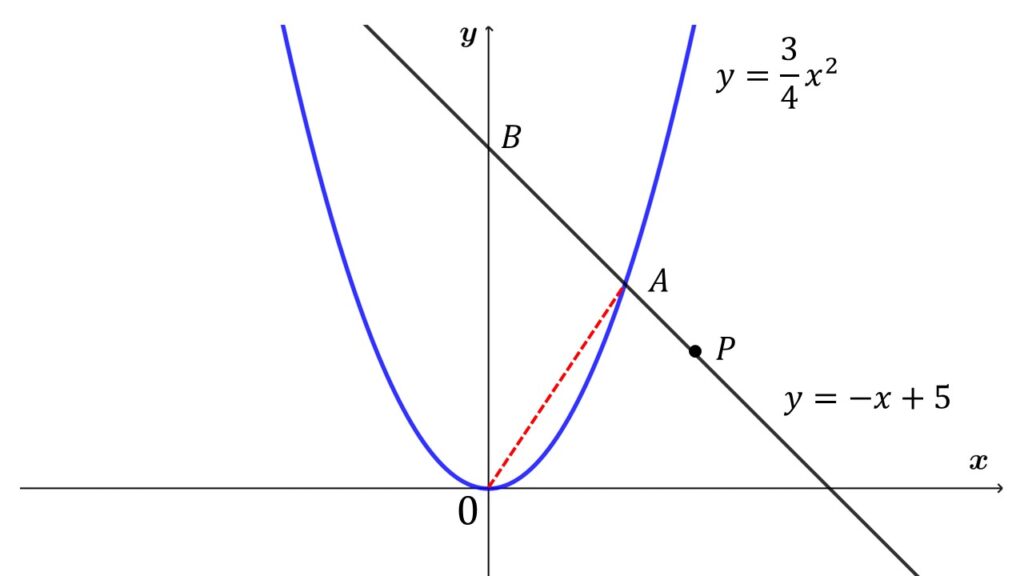
基本例題3

図のように放物線$y=\dfrac{3}{4}x^2$と直線$y=-x+5$がある。放物線と直線の交点で、$x$が正の範囲のものを$A$とし、$y=-x+5$の$y$軸との交点を$B$とする。
$(1)\:$点$A$の座標を求めよ。

$(2)\:\triangle OAB$の面積を求めよ。

$(3)\:$直線$y=-x+5$上を動く点$P$がある。
$\quad\triangle OPB$の面積が$\triangle OAB$の面積の$\dfrac{1}{2}$となるとき、点$P$の座標を求めよ。

考え方
$(1)\:$冒頭に書いた通り、交点の座標は連立方程式として求められます。
$(2)\:y$軸を底辺とみなします。つまり$\triangle OAB$の$OB$を底辺と考えます。
$(3)\:$「三角形の面積は、底辺の長さが同じなら高さに比例する」これを適用します。ならば「何を高さ」とするか？この問題の最大のポイントです。

解答
$\begin{align}(1)\quad &\begin{cases}\;y=\dfrac{3}{4}x^2\\\;y=-x+5\end{cases}\end{align}$
$\begin{align}\quad\:\dfrac{3}{4}x^2&=-x+5\\\\3x^2&=-4x+20\\\\3x^2&+4x-20=0\\\\x&=\dfrac{-4\pm\sqrt{4^2-4\times3\times(-20)}}{2\times3}\\\\x&=\dfrac{-4\pm\sqrt{16+240}}{6}\\\\x&=\dfrac{-4\pm\sqrt{256}}{6}\\\\x&=\dfrac{-4\pm16}{6}\\\\x&=\dfrac{-2\pm8}{3}\\\\x&=2\:,\:-\dfrac{10}{3}\end{align}$
$\quad A$の$x$座標は正の範囲なので$x=2$

$\quad5\times2\times\dfrac{1}{2}=5$

解説
放物線と直線がつくる図形問題では、三角形の面積を求める問題へと発展させていくパターンが半ばお約束です。
また、そこから面積を変える点の座標を求める問題へ発展させていくというのよく見られます。
基本例題ではまさにそのパターンに沿った形での出題としました。

$三角形の面積=底辺\times高さ\times\dfrac{1}{2}$

三角形の面積を考えるときはこの式をどうやって使うか考えます。
このパターンの問題では、$y$軸を三角形の底辺とみなすことがよくあります。
$y$軸が底辺ならば、高さは各点の$x$座標となります。

底辺といえば横の長さが通常でしたが、本問のように、図の見方を変えて縦の長さを底辺とすることにも慣れておきましょう。

それにどうしても慣れなかったら、自分の首を$90$°回転させて$y$軸が横になってるようにして見てください。