数学の図形問題では、補助線を引かないと解答が進まない問題も出てきます。
ただそのような問題で解答とは無関係な補助線を引いてしまったり、あるいは補助線の引き方そのものに気づけなかったりすると、たとえどんなに図形の知識が身についていたとしても残念ながら得点できないという、最悪の事態にもなってしまいます。
ならばどんな時にどんな補助線を引けば良いのか?
このページでは補助線を引くコツや補助線を引くパターンを紹介していきます。
補助線を引くコツ
補助線はある程度の見通しをつけて引くようにします。
以下の点をおさえながら補助線を引いてみると良いでしょう。
- 補助線を引くことで三角形や四角形などの簡単な図形ができる
- 補助線を対角線として考える
- 既にある直線に平行な直線を引いて同位角や錯角を考える
- 円やおうぎ形の半径や直径として考える
- 補助線を引くことである部分の長さを特定できる
- 補助線を引くことで$30°,45°,60°,90°$等の角ができる
これらが全てではありませんし、これらのように補助線を引けば必ず問題が解けるということでもありません。ただ、図形問題で解答に困ったら試してみる価値はあります。
でも1つ強調しておきたいのは、上記の事柄は暗記しないでください。
暗記するのではなく、自然と思い浮かぶようになるのが理想です。
そのためには、
単純な図形を見て何か欠けている部分はないか、
もしかけていたらどうなれば1つの図形として完成するのか
などを考えると、補助線を引くコツを身につけるトレーニングになると思います。
もっとも問題への慣れも補助線を引くひらめきの要素になります。
簡単な問題を多く解いたり、1つの問題をいろいろな解き方で考えてみることも、補助線を引くコツを身につけるには大切です。
補助線を引くにはセンスが必要なのか?
図形問題を苦手にしている人からよく、
「センスがないから補助線なんて思いつかないよ、はぁ」
なんてセリフを耳にします。
まぁ、確かに少しはセンスも必要ですがそれはごく限られた場合であって・・・。
例えば次の図を見てください。
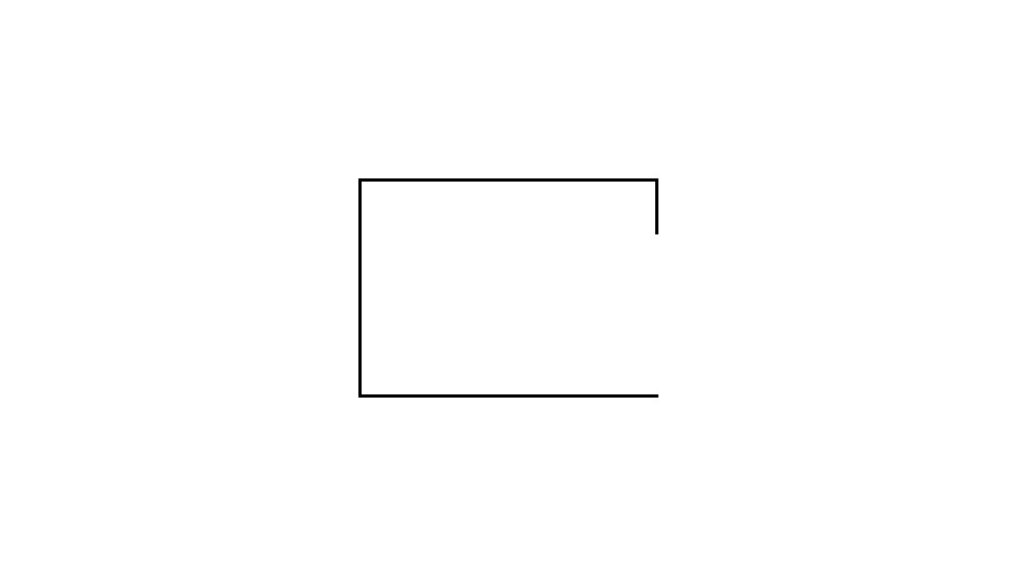
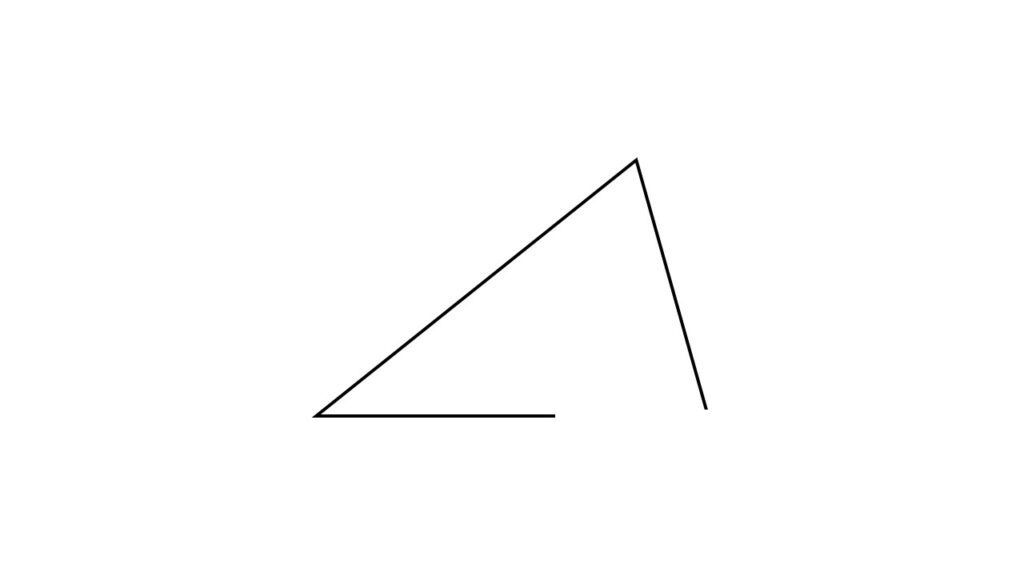
何か感じましたか?
一部の線が欠けているから四角形や三角形ではないですよね。
ただ、四角形や三角形のように感じた人は補助線を引くセンスがあると思います。
というのは、四角形や三角形ではないのに四角形や三角形みたいだと感じた時点で、頭の中では補助線を引いていることになるからです。
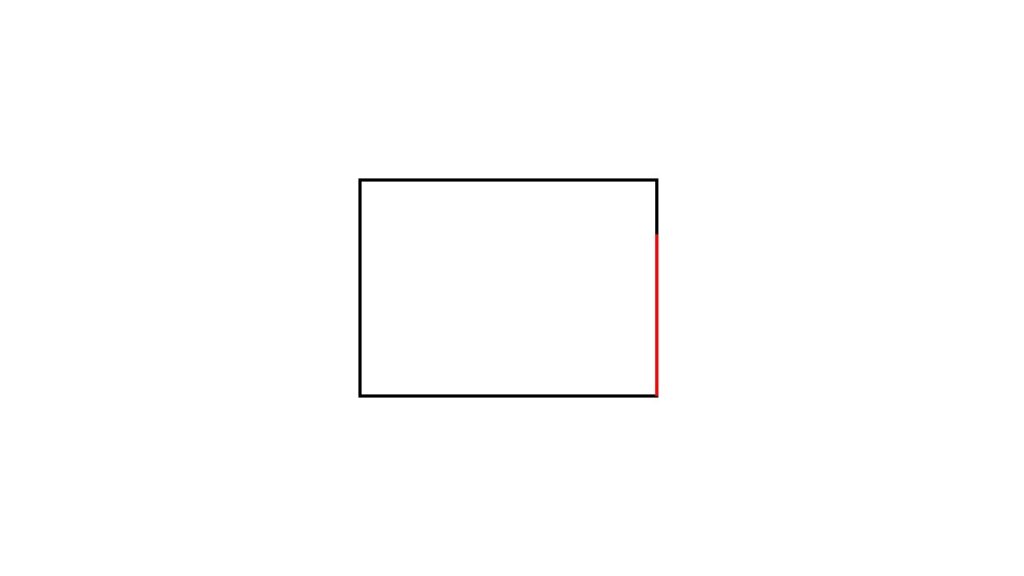
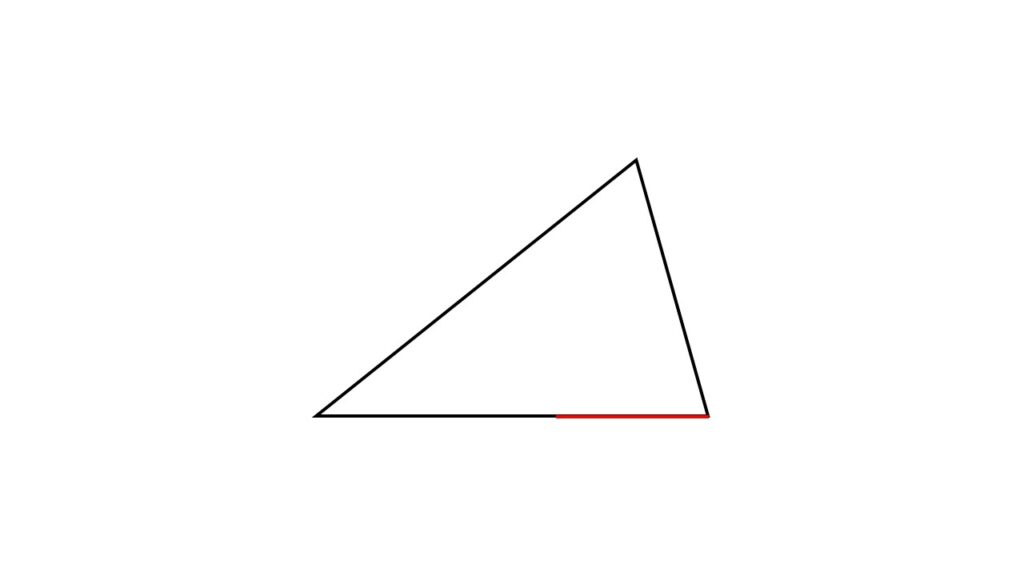
図形を完成させようとした時点でセンスがある
本来存在しないものに対し、意識的であれ無意識的であれ線を補って1つの図形として完成させている。
これって実はかなりレベルが高いことなのです。
例えばこの図。
もし補助線を引くとしたら、どこにどんな補助線を引きますか?
思いつくだけ補助線を引いてみてください。どこにどう引くのが正解だというのはありませんが、人それぞれ様々な補助線が引けると思います。

例えばパンケーキ。
友だち4人で分けて食べるとき、どんな切り方をしますか?
けんかにならないように、形はともかく、全て等しい量になるように切るものとします。
とはいえ、いくら何でもこんな切り方はしないですよね?
こんな切り方ではけんかが起きます。
パンケーキは美味しいけど友だちとは気まずくなります。
(これは色々な意味でセンスがない)

おそらくパンケーキの中心を基に、こんな感じで切り分けるはずです。

このパンケーキの例だってしっかり補助線を引いているわけです。
実際ピザカッターとかで予め線を引いてから切るでしょ?
補助線を引くことで円形のパンケーキをおうぎ形に変形させています。
その補助線を引くときって、別にセンスとかではないですよね?
切るときに料理のセンスとかは必要かもしれないけど。
補助線の日常の具体例としてパンケーキで考えてみましたが、他にも補助線を引くこと自体は日常でも普通にやってるはずなんです。普通過ぎるから気づけてないだけで。
ということで長くなりましたが、補助線を引くのにセンスが必要かどうかはあまり関係ないかと。
センスは必要ないのですが、ただ実際数学の図形問題を解いていく上で「こんな図を見たらあんな補助線を引くとうまくいく」みたいなハウツーはあります。
次によくある代表的な補助線のパターンを確認しておきましょう。
よくある代表的な補助線のパターン
冒頭に挙げた補助線を引くコツを基に、パターン化されている補助線を見ていきます。
- 補助線を引くことで三角形や四角形などの簡単な図形ができる
- 補助線を対角線として考える
- 既にある直線に平行な直線を引いて同位角や錯角を考える
- 円やおうぎ形の半径や直径として考える
- 補助線を引くことである部分の長さを特定できる
- 補助線を引くことで$30°,45°,60°,90°$等の角ができる
コツの上4つ分についてのパターンを挙げます。
残りのコツについては問題によってそれぞれ違ってくるのでパターンとしては挙げられません。都度問題を解きながら身につけてください。
補助線を引くことで三角形や四角形ができる

この形は教科書などによくある図形です。
次のように補助線を引くと良いでしょう。


補助線を引いたことで簡単な図形(三角形)ができ、角度について考えやすくなります。
補助線を対角線として考える

対角線を引くことで三角形を作ります。
五角形や六角形で対角線を引くと考えやすくなることがあります。


平行線を引いて同位角や錯角を考える

単純に平行四辺形に補助線として平行線を引くことはあまりありませんが、次のような図形で平行線を引くと効果が大きいです。


既にある平行線に、さらに平行線を引いて考えるものもよく出題されます。


円やおうぎ形の半径や直径として考える
円やおうぎ形が出題されたら、反射的に半径や直径を書き込むようにしておきましょう。

例えば図のように円周角を考えている時に



のように補助線を引いて円周角や中心角を考えます。
実際の問題ではもう少し線が引かれている状態から補助線を自分で引いていくため、複雑に見えてしまったり、補助線に気づけなかったりしてしまいます。注意が必要です。
補助線を引くことである部分の長さを特定できる
これは問題ごとに都度補助線の引き方が変わってくるので、例を挙げるときりがありません。ただ、

補助線を引くことで図のような状態がどこかにできるようにすると上手くいくことがあります。
例えばこんな感じで。


三角形の合同や三角形の相似の応用で、辺の長さや面積を求める時にこの形を使って考えます。
詳しくは他のページで都度紹介するので、ここでは「そんな引き方もあるのね」程度で軽く覚えておいてください。
隠れた条件を見つけるために補助線を引く
図形問題では、問題文や図に書かれていない隠れた条件を自分で見つけ出すことも必要になってきます。
その「隠れた条件を見つけ出す手段の1つとして補助線を引いてみる」わけです。
パンケーキの所でも書きましたが、補助線を閃くのに確かにセンスも少しは必要です。
でもそれは本当に難しい問題を解くときであって、補助線を引くパターンに照らして考えると何とか対応できるものがほとんどです。
なので逆に言えばパターンを身につければ補助線を必要とする図形問題のほとんどは解答できると。
で、パターンを身につけるにはやはり多くの問題を解いていくしかありません。
パターンを身につけたらきっと感じるはずです。
補助線はセンスだと思ってたけど練習の積み重ねなんだな、と。
