ここでは比例の中でも特に重要な「比例定数」について詳しく紹介します。
比例定数は、中2で学ぶ一次関数や中3で学ぶ関数$y=ax^2$の「変化の割合」の基本になるものです。
中1の段階では変化の割合という言葉を学びませんが、比例定数を理解しておけば変化の割合も簡単に理解できます。
ということで比例定数を徹底理解していくのは当然として、今後変化の割合を学ぶ際に少しでも理解しやすい様に少し深めに解説していきます。
比例定数の基本
比例定数とは、比例の式$y=ax$で$a$のことです。
$y=3x$という式があったら比例定数は$3$
$y=-3x$という式があったら比例定数は$-3$です。
例として、$y=3x$を使って比例定数を詳しく見ていきます。
次の表は$y=3x$の関係を表したものです。
| $x$ | ・・・ | 1 | 2 | 3 | 4 | 5 | ・・・ |
| $y$ | ・・・ | 3 | 6 | 9 | 12 | 15 | ・・・ |
比例だから$x$の値が2倍、3倍・・・となると、それに伴い$y$の値も2倍、3倍・・・となっています。
そして当たり前のことですが
$x$が1増えると、$y$は3増えています。
この当たり前のことが後々大きな意味を持ってくるので、当たり前と思わずにスゴく大切なことを学んだと思ってください。
もう1つ例として、$y=-3x$についても見てみます。
| $x$ | ・・・ | 1 | 2 | 3 | 4 | 5 | ・・・ |
| $y$ | ・・・ | -3 | -6 | -9 | -12 | -15 | ・・・ |
比例定数が負の値だとしても、$x$の値が2倍、3倍・・・となると、それに伴い$y$の値も2倍、3倍・・・となっています。そして
$x$が1増えると、$y$は3減っています。
($x$が1増えると、$y$は$-$3増えているとも言えます)
この『$x$が1増えると、$y$はいくつ増えているか』を表しているのが比例定数$a$というわけです。

比例の式 $y=ax$ の$a$のことを比例定数という。
比例定数は、$x$が1増えると$y$はいくつ増えるか(減るか)を表している
このことを覚えておくと、比例のグラフをかくときに少しラクできます。
比例定数の求め方
次に比例定数の求め方を確認します。
とは言っても何ら難しいことではない。
$y=ax$の関係が比例だから、単純に$\dfrac{y}{x}$を計算するだけです。
比例定数を求める問題は主に3つのパターンがあります。以下それぞれのパターンを見ていきます。
●パターン1 表から比例定数を求める問題●
代表的な問題として、比例の表が与えられてそこから比例定数を求めるものがあります。
| $x$ | ・・・ | 1 | 2 | 3 | 4 | 5 | ・・・ |
| $y$ | ・・・ | -3 | -6 | -9 | -12 | -15 | ・・・ |
例として、この表から比例定数を求めてみます。
比例を考える時は常に$y=ax$を頭の片隅に置いておくように。
表から$x$が$1$のとき$y$は$-3$とわかります。
なのでそれぞれ$x$と$y$に代入して
$-3=a\times1$ つまり $a=-3$と求まります。
$x=1$ $y=-3$ のときを考えましたが、表から読み取れる値ならどれでも構いません。
もし$x=4$のとき$y=-12$であることを考えたいのなら、
$-12=a\times4$
$4a=-12$
$a=-\dfrac{12}{4}$
$a=-3$ と求まり、やはり比例定数は$-3$とわかります。
●パターン2 文章だけで出題される問題●
具体的には次のような文で出題されます。
$y$は$x$に比例し、$x=4$のとき$y=8$である。このときの比例定数を求めよ。
解答は単純に、$y=ax$の$x$と$y$に問題の条件をそのまま当てはめるだけです。
$8=a\times4$
$4a=8$
$a=\dfrac{8}{4}$
$a=2$ です。
●パターン3 グラフから通る点の座標を読み取り計算する問題●
与えられたグラフから比例定数を求める問題もあります。
ただこの場合、比例の式を求める問題が多くなります。
具体的には次のように出題されます。
グラフから比例の式を求めよ。

この場合、問題は「比例の式を求めよ」ですが、比例定数を求めることになります。
グラフが通る点の座標を実際に読み取り、$y=ax$に通る点の座標を代入します。
読み取る座標は原点以外ならどこでも構いません。
このグラフでは、$(1,3)$を通ることがわかるので
$3=a\times1$
$a=3$ となり比例定数は$3$とわかります。
もちろん比例の式は$y=3x$です。
3パターンをあげましたが、比例定数の求め方は実際の所、どれも同じです。
通る点の座標を$y=ax$の$x$と$y$に代入して$a$を求める。
この流れで求めます。
通る点の座標が
表で示されているか、
文章として示されているか、
グラフで示されているか、
の違いだけです。
ここまで比例定数について解説してきましたが、次に比例定数から少し離れ比例のグラフのかき方を確認していきます。
比例のグラフのかき方
比例のグラフをかくときはグラフが通る点の座標を求めろ!!
唐突に書きましたが、比例のグラフをかくときはこの一言に尽きます。
ではどうやって通る点の座標を求めるのか?
そこに注目しながら読んでください。
●グラフのかき方 基本パターン●
比例のグラフは2つの手順でかいていきます。

比例のグラフをかく手順(基本パターン)
①グラフが通る点の座標を求める
そのために$y=ax$の$x$に適当な数値を代入して$y$の値を求める
②原点と①の点を直線で結ぶ
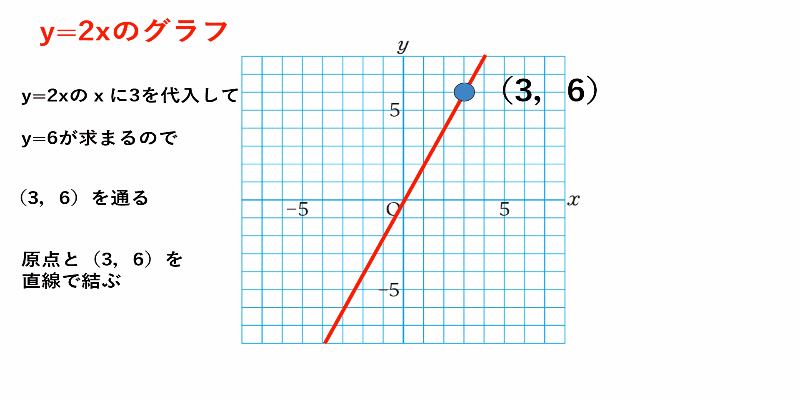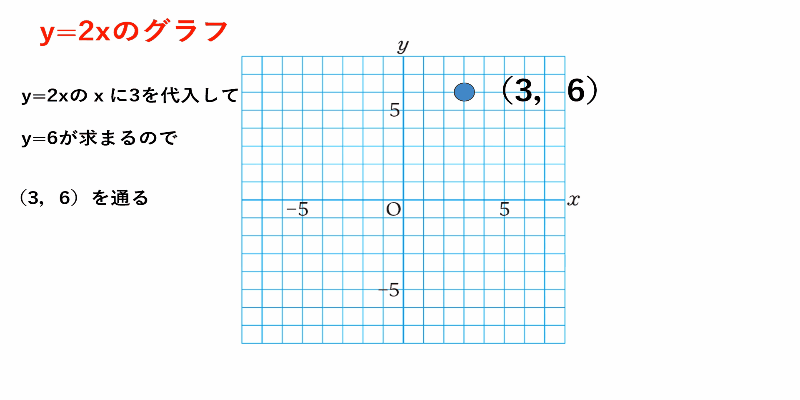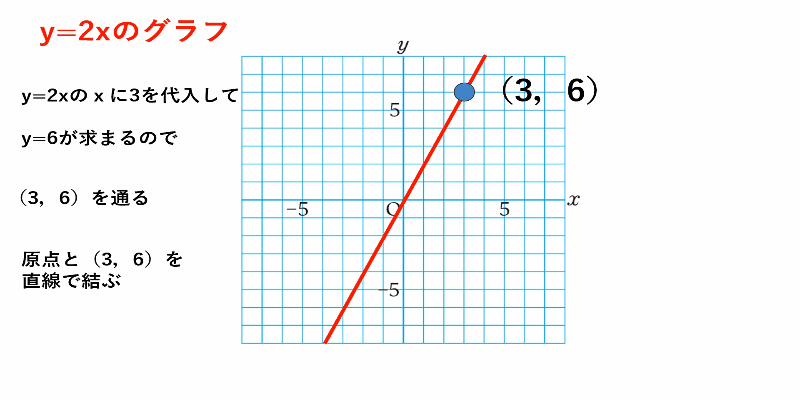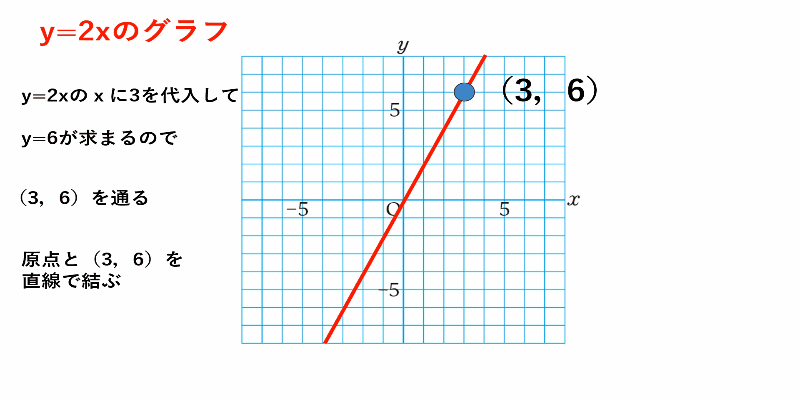
この手順をふまえ、例として$y=2x$のグラフかき方を見てみましょう。
$y=2x$のグラフ
①グラフが通る点の座標を求めるために、$x$に$3$を代入
$y=2\times3=6$
これより$(3,6)$を通ることがわかる
②原点と$(3,6)$を直線で結ぶ
例では$x=3$として計算しましたが、$x$に$1$でも$2$でも$-3$でも、適当に好きな数値を代入して通る点を求めて構いません。
このように、通る点の座標を計算で求めて原点と直線で結ぶグラフのかき方は、最も基本的な考え方なので必ずこの理屈を覚えておいてください。
ところで、グラフのかき方のサブタイトルで「基本パターン」と書きました。
「基本パターン」というからには、基本じゃないパターンがあるのか!! と思うかもしれませんが、その基本じゃないパターンはあります。
基本じゃないパターンを知っておくと、グラフをかくときにちょっとだけ横着できます。
ということで次に、ちょっとだけ横着できるパターンを見ていきます。
●グラフのかき方 横着パターン●
横着パターンで必要になってくる考え方が、このページの最初に学んだ比例定数の性質です。
重要なので改めて載せます。

比例の式 $y=ax$ の$a$のことを比例定数という。
比例定数は、$x$が1増えると$y$はいくつ増えるか(減るか)を表している
特に、$x$が1増えると$y$はいくつ増えるか(減るか)を考えることが横着のポイント。
比例のグラフをかくときには、原点のほかに通る点の座標がわからないとかけません。
その通る点の座標を、比例定数を使って求めていこうというわけです。
比例定数を使って考えれば、計算することなくグラフをかけます。
では実際に$y=3x$のグラフのかき方を見ていきましょう。
$y=3x$のグラフ
①グラフが通る点を求めるために比例定数の性質に着目
②原点と$(1,3)$を直線で結ぶ
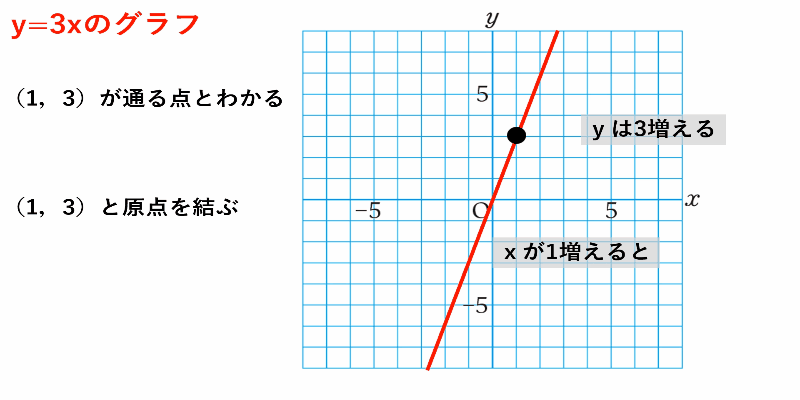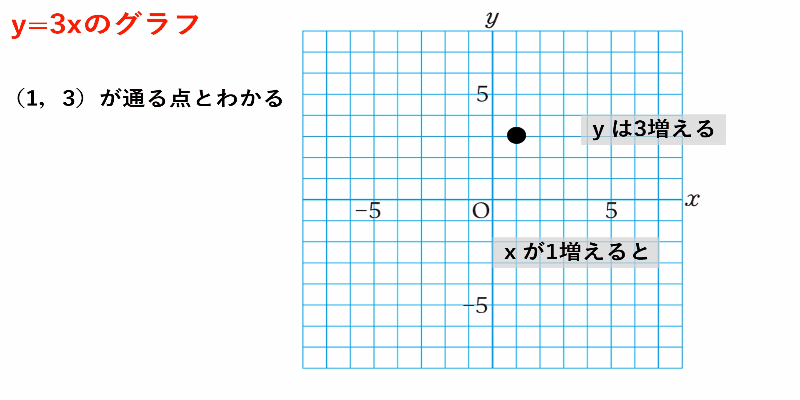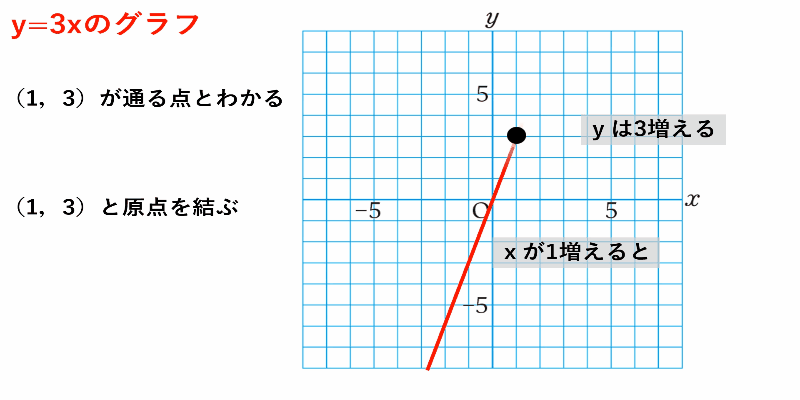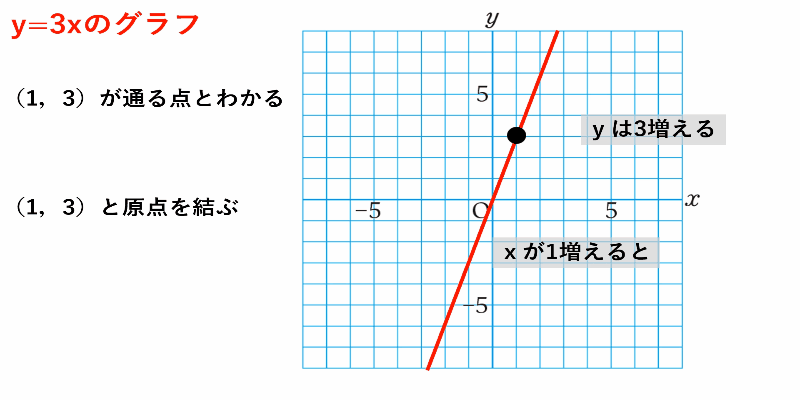
比例定数の性質を使って考えると、計算しないで済む分計算ミスも防げます。
横着できてしかもミスも防げる!!
グラフをかくときは比例定数に注目して横着しましょう。ただ、基本パターンの理屈はしっかり覚えておきましょう。
参考までに、比例定数が負の時の横着したグラフのかき方も見ておきましょう。
$y=-3x$のグラフ
①グラフが通る点を求めるために比例定数の性質に着目
②原点と$(1,-3)$を直線で結ぶ

比例のグラフのかき方を見てきました。
横着パターンのかき方を知っておくと、中学2年生が学ぶ一次関数のグラフをかくときにとても役立ちます。
繰り返しますが、基本パターンを知った上で横着パターンを使いましょう。
次に比例定数が分数のときのグラフをかく練習をします。
でもその前に比例定数に話を戻し、もう少し深く比例定数を理解していきます。
その後に比例定数が分数のグラフのかき方を練習します。
比例定数が分数のとき
比例定数を求めるには、単純に$\dfrac{y}{x}$を計算すれば良いことは先に書きました。
そして比例定数の意味は、$x$が1増えると$y$がいくつ増えるか(減るか)ということでした。
このことを関連させて、改めて$y=3x$を考えてください。
$y=3x$の比例定数を分数にすると
$y=\dfrac{3}{1}x$ です。
比例定数はいくつだかわかりますよね? 当然$3$です。もちろん$\dfrac{3}{1}$でもあります。
では$y=\dfrac{6}{2}x$ の比例定数はいくつかというと・・・、
当然$3$であって、$\dfrac{6}{2}$でもあって、約分できるから$\dfrac{3}{1}$でもあります。
ということは

比例定数を分数で考えたとき
比例のグラフは、$x$が分母の数だけ増えると$y$は分子の数だけ増える点の座標を通る
といえます。
既に示した$y=3x$のグラフを見てみると、$x$が$2$増えると$y$は$6$増えた点の座標を通っていることがわかります。
このことをふまえると、$y=\dfrac{3}{2}x$のように、比例定数が約分できない分数のときでも簡単にグラフをかくことができます。
この場合、$x$が$2$増えると$y$は$3$増える点の座標を通ることがわかります。
実際にグラフのかき方を見てみましょう。
大事なことだから何度も書きますが、比例のグラフをかくときは原点とグラフが通る点の座標を直線で結びます。
その通る点の座標を求めるためにふつうは計算をするわけですが、比例定数に注目すると計算することなく求めることができます(横着できる)。で、横着するためには比例定数を分数にするとわかりやすいということ。
そしてこれから練習するのが、比例定数が分数になっているグラフです。
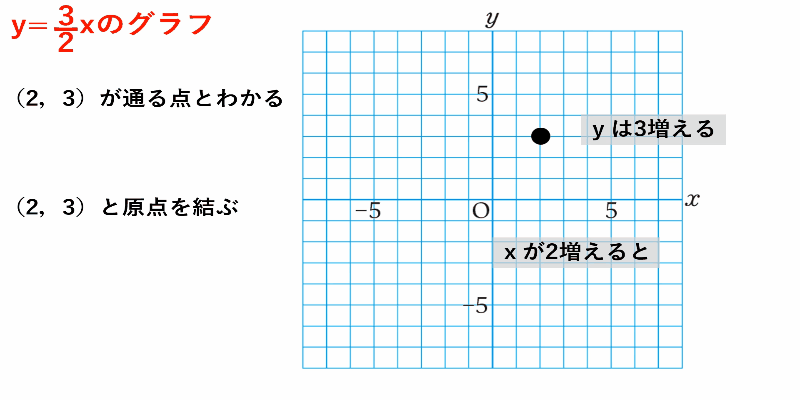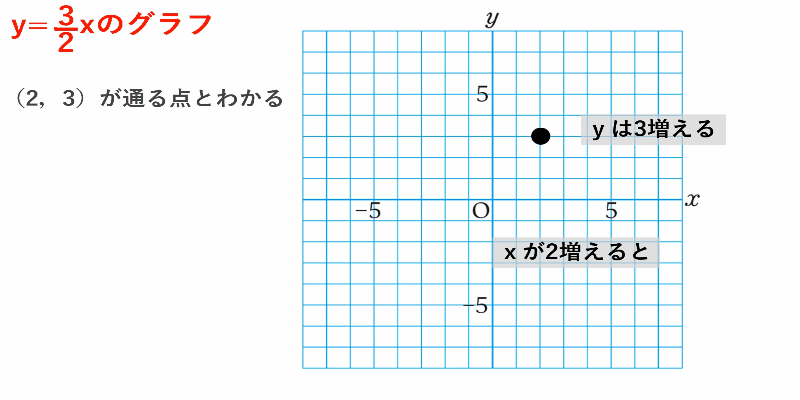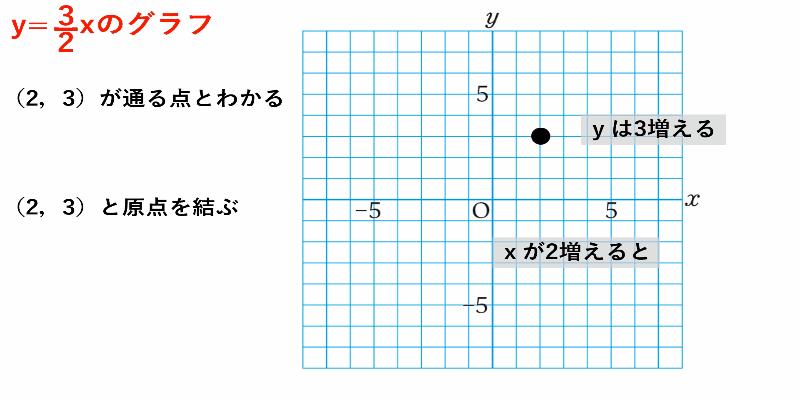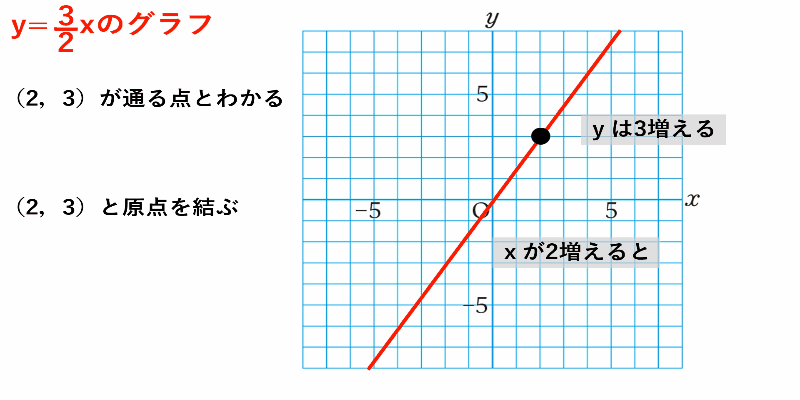
$y=\dfrac{3}{2}x$のグラフ
①グラフが通る点を求めるために比例定数の性質に着目
($x$が$2$増えると$y$は$3$増える)
②原点と$(2,3)$を直線で結ぶ
ここまでのことを応用すると、比例定数が小数のときも簡単にグラフをかくことができます。
小数を分数に直して分母と分子に注目すれば、後は解説してきた通りです。
練習として、$y=1.5x$のグラフをかいてみてください。

