比例とは
例えば、1個10円のお菓子を1個買ったら10円、2個買ったら20円、3個買ったら30円・・・という様に、お菓子の個数が2倍、3倍・・・となると、代金も2倍、3倍・・・となります。
このとき「お菓子の代金は個数に比例している」といいます。
そして 代金=1個の値段×個数 という式が作れますね。
別の例で
道のり=速さ×時間 も比例の関係にあります。
速さが一定だとしたら、道のりは時間に比例します。
時間が一定だとしたら、道のりは速さに比例します。
このように一方の値$x$が2倍3倍・・・となると、それに伴い、もう一方の値$y$も2倍3倍・・・となる関係のことを比例といいます。
「$y$は$x$に比例する」という言い方が頻繁に出てくるので覚えておきましょう。
比例の式と比例の具体例
比例の関係は
$y=ax$という式で表せます。
この形の式を比例の式といいます。
お菓子の例では、$y$が代金 $x$が個数 です。
$a$は1個の値段という定まった値です。
速さの例では、
速さが一定だとしたら$y$が道のり、$x$が時間です。$a$は速さになります。
時間が一定だとしたら$y$が道のり、$x$が速さです。$a$は時間になります。
上記の例からもわかる通り、$a$には定まった値(一定の値)が当てはまります。
この$a$のことを「比例定数」といいます。とても重要なことばなので覚えておきましょう。
確認問題
次の中で比例の関係にあるものを全て選びなさい。
(1)5の段のかけ算九九
(2)よしお君の身長$x$と体重$y$の関係
(3)底辺が18cmの三角形の、高さ$x$と面積$y$の関係
(4)水槽に毎分5ℓずつ水を入れる時の、時間$x$とたまる水の量$y$の関係
(5)イケメン君の告白回数$x$と告白成功回数$y$との関係
解答
(1)(3)(4)
(1)5の段といわず、かけ算九九は比例の関係にあります。
(2)身長が2倍、3倍・・・となっても体重が2倍、3倍・・・となるとは限りません。よって比例の関係ではありません。
(3)三角形の面積$=\dfrac{1}{2}\times$底辺$\times$高さ
この問題の場合
$y=\dfrac{1}{2}\times18\times$$x$ となり、約分まで進めると
$y=9x$ で比例の式の形になっています。文字式なので、簡単にできるところまで計算を進めて判断します。
ということは、三角形の面積は底辺が一定ならば、高さが2倍、3倍・・・となると面積も2倍、3倍・・・となることがわかります。
(4)$y=5x$の式が作れるので比例の関係です。
(5)たとえイケメンでも告白の仕方がヘタだと成功しません。よって告白回数と成功回数には何ら関係はありません。というより、そもそもイケメンって何よって話です。


$y$は$x$に比例するとき
$y=ax$ ($a$は比例定数)
という式で表せる
比例の関係では必ず$y=ax$の式が作れます。
そして比例の関係を考える時は$a$にはどんな値が当てはまるのかがとても重要になります。
次にこの比例定数$a$を求める練習をします。
比例の基本問題
比例がどんなものなのかがわかったところで、テストで絶対に正解できるようになっておきたい代表的な問題を確認します。
基本例題1 次の問いに答えよ。
(1)$y$は$x$に比例し、$x=5$のとき$y=30$になる。$y$を$x$の式で表せ。
(2)$y$は$x$に比例し、$x=7$のとき$y=-56$になる。$y$を$x$の式で表せ。
(3)$y$は$x$に比例し、$x=3$のとき$y=5$になる。$y$を$x$の式で表せ。
考え方 この問題は比例の問題を解くときの全ての基本になります。必ず正解できるように解き方の流れを覚えてしまいましょう。
「$y$は$x$に比例し」と問題文にあった時点で$y=ax$と考え、「$y$を$x$の式で表せ」との設問には必ず$y=$~$x$の形で答える
↓
問題文に必ず条件が出ているので、$x$や$y$にそれぞれ数値を代入
↓
比例定数$a$を求める
↓
$y=ax$の$a$に求めた比例定数をあてはめる
この手順で解きます。
要するに、比例定数を求めてそれを当てはめるだけです。
解答
(1)$y=ax$とおく。
$x=5$、$y=30$ をそれぞれ代入すると
$30=5a$
$a=6$
よって求める比例の式は $y=6x$ となる。
(2)$y=ax$とおく。
$x=7$、$y=-56$ をそれぞれ代入すると
$-56=7a$
$a=-8$
よって求める比例の式は $y=-8x$ となる。
(3)$y=ax$とおく。
$x=3$、$y=5$ をそれぞれ代入すると
$5=3a$
$a=\dfrac{5}{3}$
よって求める比例の式は $y= \dfrac{5}{3}x$ となる。
繰り返しますが、この問題は全ての比例の問題の基本になります。
解き方をそのまま覚えてしまってください。
基本例題1と同じタイプの問題で、次のように出題されることもあります。
基本例題2
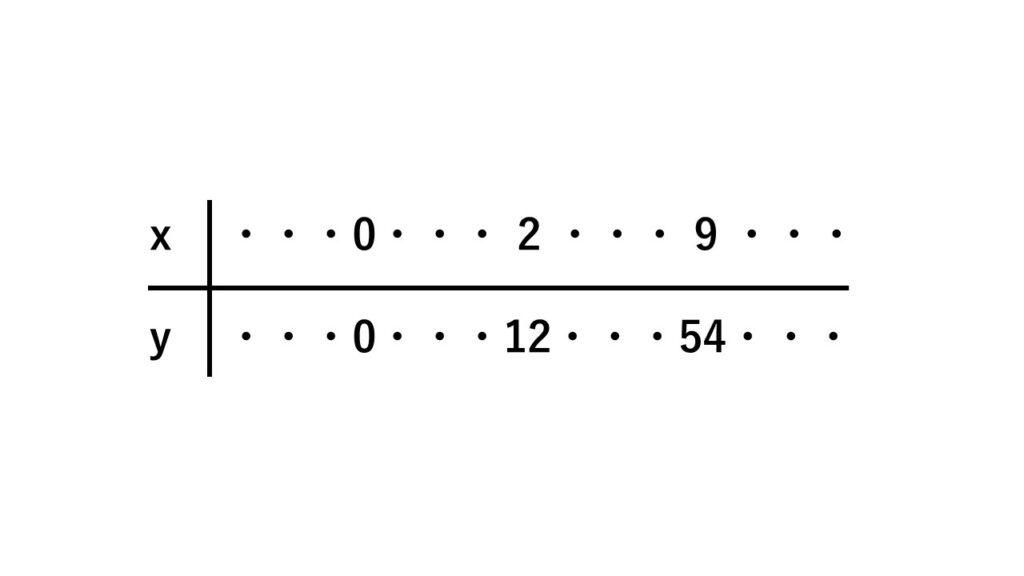
$y$は$x$に比例し、次の表の関係がある。
(1)$y$を$x$の式で表せ。
(2)$y=-54$のときの$x$の値を求めよ。
考え方
(1)基本例題1と同じ考え方です。基本例題1では言葉で表されていたものが、基本例題2では表で表されただけの違いです。
(2)(1)の結果を使い、$y=-54$を代入すれば求められます。
解答
(1)$y=ax$とおく。
表から $x=2$ のとき $y=12$ だから
$12=a\times2$
$12=2a$
$a=6$
よって $y=6x$
補足 $x=9$、$y=54$を代入して求めても良い。もちろん結果は同じ。
(2)(1)の結果から$y=6x$ に $y=-54$ を代入すると
$-54=6x$
よって $x=-9$
補足 この例題のように、比例の式を求めてから$x$や$y$の値を求めるパターンの問題は、定期テストでよく出題されます。
最初の問題で間違えると連鎖的に次の問題も間違えるので、比例の式を確実に求められるようにしておきましょう。

・「$y$は$x$に比例し」と問題文にあった時点で$y=ax$と考える
・「$y$を$x$の式で表せ」との設問に対しては必ず$y=$~$x$の形にして答える
