ここでは初めて変域を学ぶ中学1年生のために、変域とは何かや、変域の不等号を使った表し方について詳しく解説します。合わせて変域の数直線での表し方も学び、変域の意味を徹底して理解していきます。
変域とは
変域とは
取り得る値の範囲 のことをいいます。
$x$の変域といわれたら$x$が取り得る値の範囲
$y$の変域といわれたら$y$が取り得る値の範囲
ということになります。
取り得る範囲を考えるからには、大小関係の比較が出てきます。
この比較をするときの記号が不等号
>< ≧ ≦
です。
不等号 > < ≧ ≦ について
不等号 > < ≧ ≦ は大きい値の方に開いた側を向けます。
> と <
例えば、
$x>5$とあったら「$x$は$5$より大きい値」のことを表します。
「より大きい」とは、「その数を含めない範囲で大きい値」という意味です。
つまり「$x$は5を含めない範囲で大きい値」となります。
$x<6$なら「$x$は$6$より小さい値」のことで「$x$は6を含めない範囲で小さい値」を表します。
「より小さい」と同じ表現として「未満」もあります。
$x<6$なら「$x$は$6$未満」としても同じ意味です。
$6>x$とあったら
「6は$x$より大きい値」となります。
でもこれ、よく見たら1つ上の例と書き方を逆にしただけでです。
つまり「$x$は6を含めない範囲で小さい値」と同じことを表しています。
大小比較をするのは数値だけに限りません。
文字の比較も数学では出てきます。
文字の比較というと違和感を持つかもしれませんが、
$x<y$なら意味は「$x$は$y$未満」という意味になります。
≧ と ≦
$x≧5$とあったら「$x$は$5$以上の値」のことを表します。
「以上の値」とは「その数を含めた範囲で大きい値」という意味です。
つまり「$x$は5も含めた範囲で大きい値」となります。
$x≦6$なら「$x$は$6$以下の値」のことを表します。
「$x$は6を含めた範囲で小さい値」ということを表します。
変域の表し方
上記のことを踏まえると、もう少し発展させた変域の表し方もできます。
「$x$は$5$より大きく$9$より小さい」とあったら
$5<x<9$ と表せます。
$9>x>5$ と表しても同じです。
「$x$は2以上$6$未満」とあったら
$2≦x<6$ と表せます。
「$x$は$y$以上$z$未満」とあったら
$y≦x<z$ と表せます。
慣れないうちは3つの文字の大小比較に違和感しかないかもしれませんが、数学の世界ではこの様な書き方はよく出てきます。
この書き方がよくわからないなら
$x$をよしお $y$を友達 $z$を恋人と置き換えて
「友達≦よしお<恋人」で考えてみてください。
「よしおは友達以上恋人未満」という意味になります。
これならいくらか覚えやすいかと思います。
それでは変域の表し方の練習をやってみましょう。
練習問題
$x$の変域が次の範囲のとき、不等号を使って表せ。
(1)$-3$以下
(2)$0$以上$8$未満
(3)$-5$より大きく$7$以下
(4)$y$は$3x$より大きい
解答
(1)$x≦-3$
(2)$0≦x<8$
(3)$-5<x≦7$
(4)$y>3x$
補足
3つ以上の数の大小比較をするときは必ず、不等号の開いている方が全て同じ方に向くように並べます。
小さい順に$a<b<c$と書くか、
大きい順に$c>b>a$と書く。
もし『$a<b>c$』と書くと
「$a$より$b$の方が大きいのはわかった」
「$c$より$b$の方が大きいのはわかった」
「じゃあ$a$と$c$ではどっちが大きいの?」
となってしまい、説明ができなくなってしまいます。
このような書き方をするとテストでは確実に×になるので気をつけましょう。
変域の数直線上での表し方
変域を考えるとき、数直線を使って表すことがよくあります。
変域を関数と絡めて考えるときにグラフの一部として表すので、数直線上での表し方のルールもおさえておきましょう。
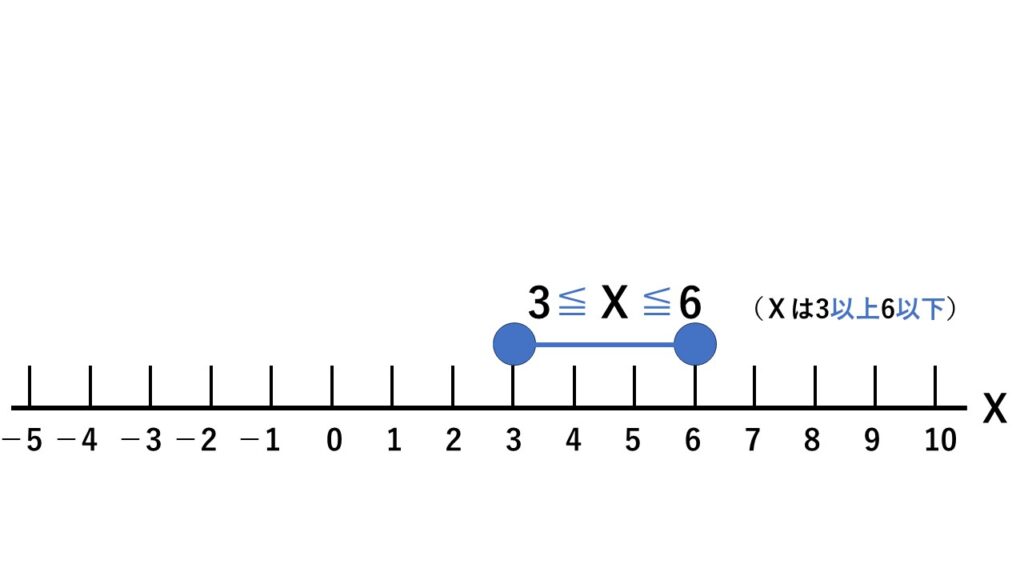
例えば、変域 $3≦x≦6$を数直線で表すときは次のように表します。
- 始まりと終わりを丸で表す
- 以上、以下のときは塗りつぶした丸にする
- 始まりと終わりを線で結ぶ
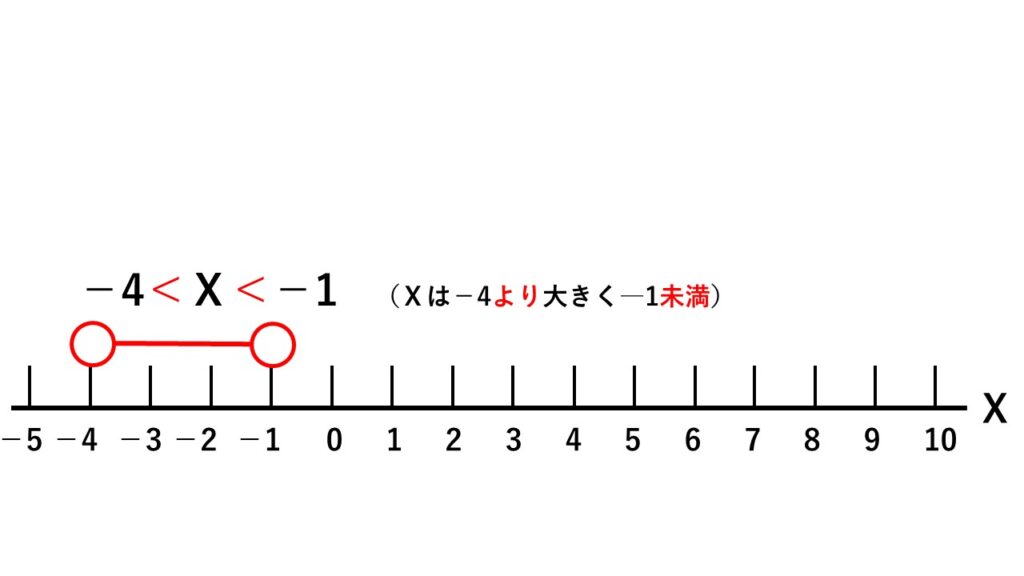
変域 $-4<x<-1$を数直線で表すときは次のように表します。
- 始まりと終わりを丸で表す
- より大きい、より小さい、未満のときは白丸にする(塗りつぶさない)
- 始まりと終わりを線で結ぶ
以上、以下のように、
「その数値を含めて考えていく場合は塗りつぶして表す」ようにします。
もちろん <や≦ を組み合わせた変域も表せます。
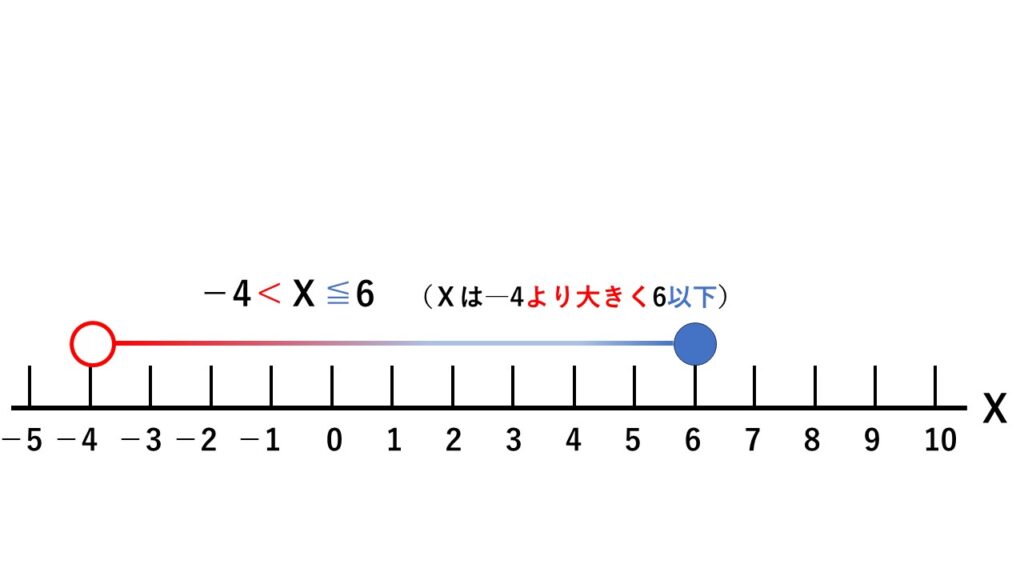
変域 $-4<x≦6$は次のようになります。
- 始まりと終わりを丸で表す
- より大きいのときは塗りつぶさない
- 以下のときは塗りつぶす
- 始まりと終わりを線で結ぶ
上記3つは始まりと終わりがある変域を例にしました。
でも変域には始まりはあるけど終わりがないものもありますよね。
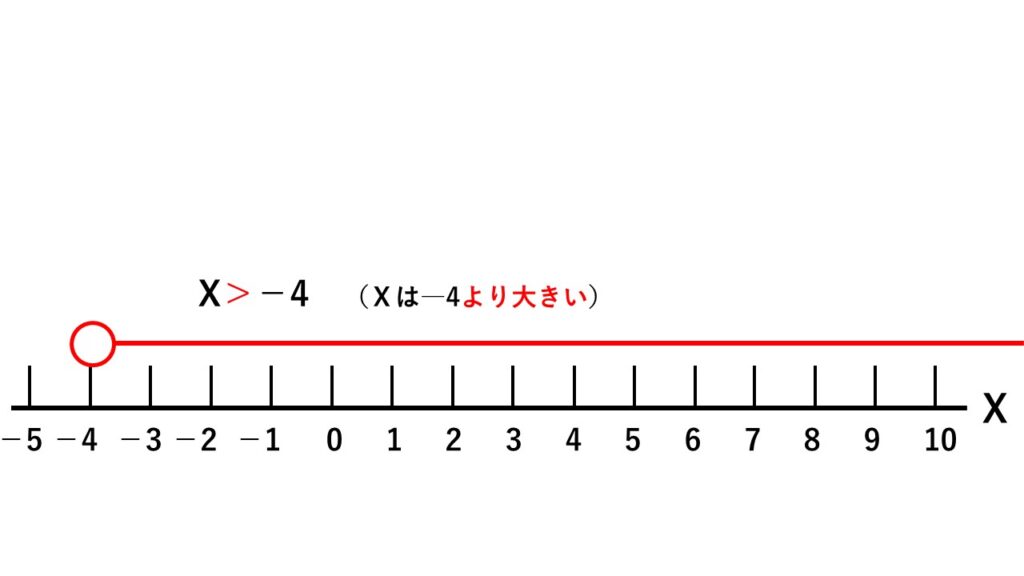
$x>-4$は「$x$は$-4$より大きい」という意味、つまり「$-4$より大きければいくつでも良い」ということなので、終わりがありません。
終わりがないから当然、数直線上でも終わりがありません。
ということで$x>-4$を数直線で表すと次のようになります。
- 始まりを丸で表す
- より大きいのときは塗りつぶさない
- 始まりの所から線を無限に引く
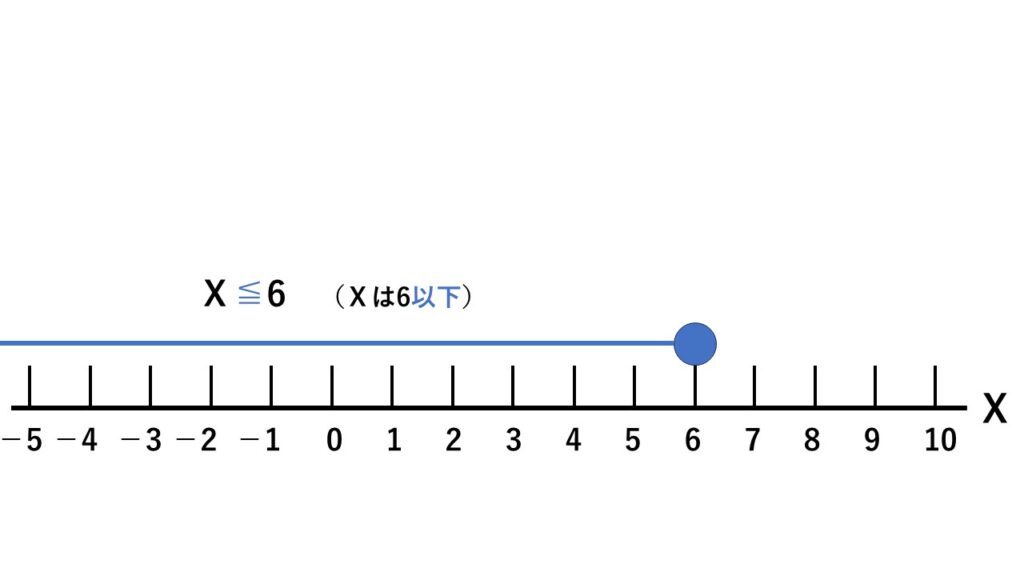
$x≦6$を数直線で表すと
- 始まりを丸で表す
- 以下のときは塗りつぶす
- 始まりの所から線を無限に引く
このように、終わりのない変域を数直線で表すときは、必ず線を引き続けるようにします。
途中で止めてしまうと全く意味が違うことになってしまうため、テストでは誤答扱いになってしまいます。
気をつけましょう。
この先関数を学んでいくと、変域と合わせて考える問題がよく出題されます。
関数ではグラフをかいていくことになりますが、そのときも始まりと終わりに〇か●をかいていきます。
詳しくは関数のページの所で扱います。
ここでは変域の数直線上での表し方のルールを覚えておきましょう。
