ここでは主に平面図形の用語とその表し方、記号について学びます。合わせて角の表し方についても確認していきます。
理解するというよりかは覚えておくべき内容なので、しっかりおさえておきましょう。
平面図形の用語と表し方
直線 半直線 線分
- 直線 始まりも終わりもない無限に続くまっすぐのびた線
通る点をアルファベットなどで示し、直線$AB$のように表す - 半直線 始まりはあるけど終わりがないまっすぐ伸びた線
半直線$AB$とあったら、Aから始まりB方向へ無限に続くもの - 線分 始まりと終わりが明確なまっすぐな線
線分$AB$とあったらAから始まりBで終わる線
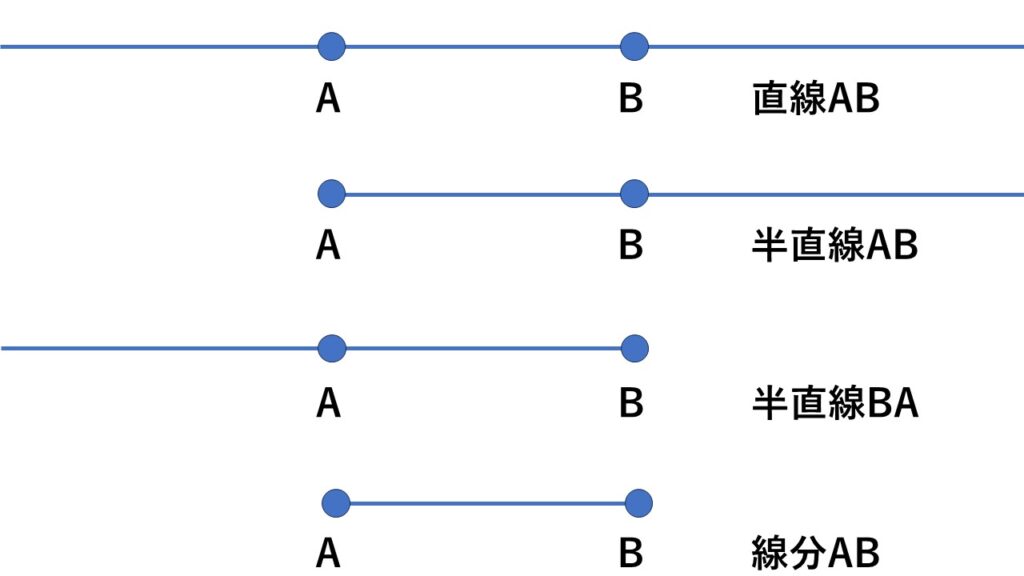
線分$AB$と線分$CD$の長さが等しいとき
$AB=CD$ と表します。
ちなみにですが、直線$EF$と直線$GH$があったとして $EF=GH$ はあり得ません。
だってそうですよね。直線は無限に続くわけだから長さの比較自体ができません。
三角形の表し方
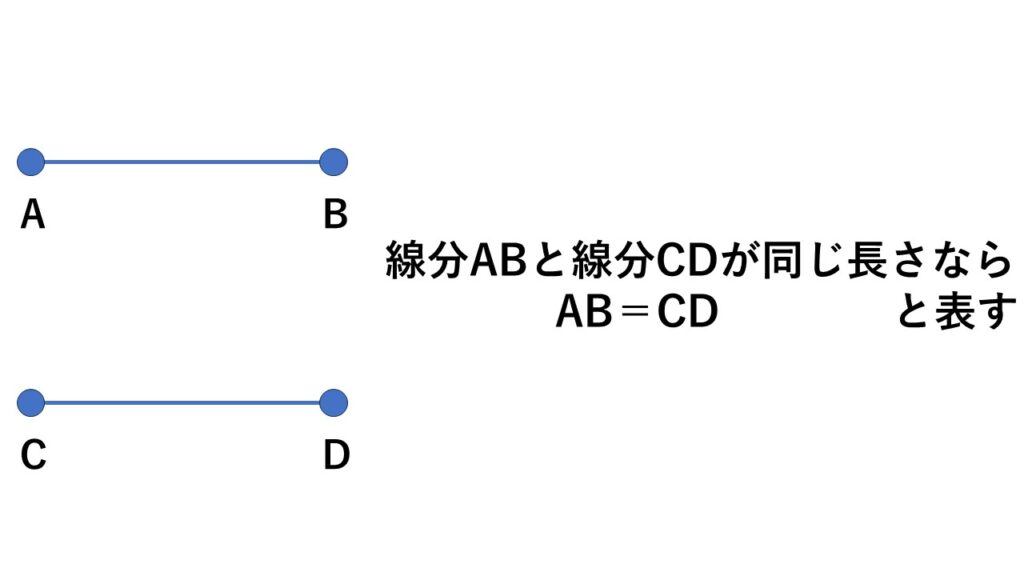
3点A、B、Cをそれぞれ頂点とする三角形を$△ABC$と表します。
もう少し正確に書くと、一番上にある頂点から反時計回りに頂点をたどっていきます。
なので、次のイラストはどちらも$△ABC$と表して間違いはないのですが、右側の三角形は$△CAB$と表した方がより正確に表したものといえます。
ちなみに三角形には正三角形や二等辺三角形、直角三角形など色々とありますが、$△$の記号だけをみてもどんな三角形なのかはわかりません。
どんな三角形なのかを特定するには、同時に示されている辺や角などの条件を参考にします。
例えば$△ABC$で$AB=BC,BC=CA,CA=AB$とあったら正三角形とわかります。
$AB$とはもちろん辺$AB$のことです。線分$AB$ともいえますね。
角の表し方
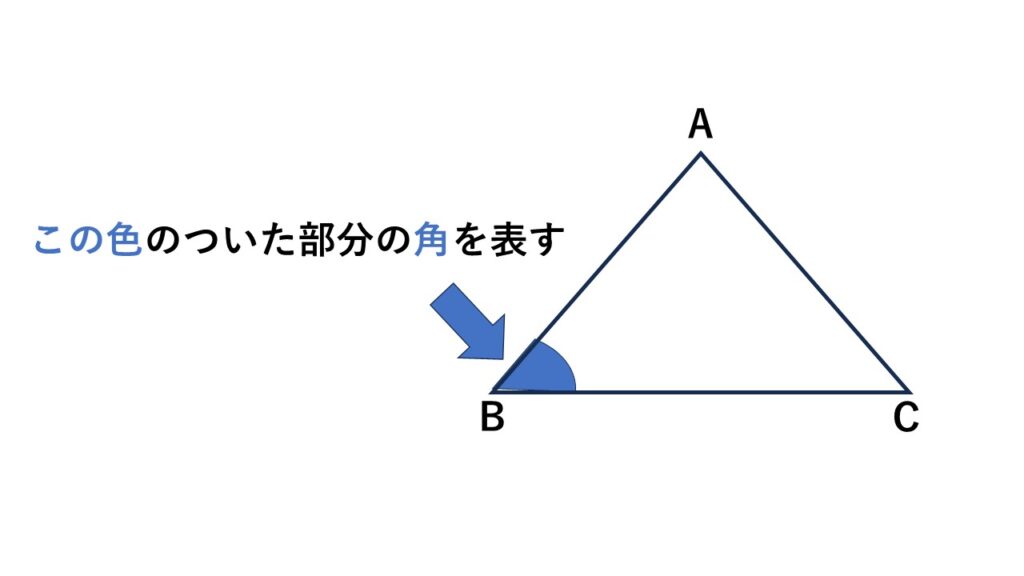
角を表すときは $∠$ を使います。
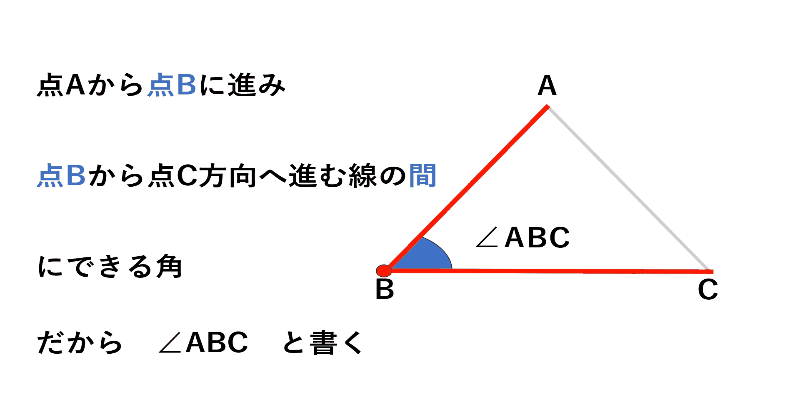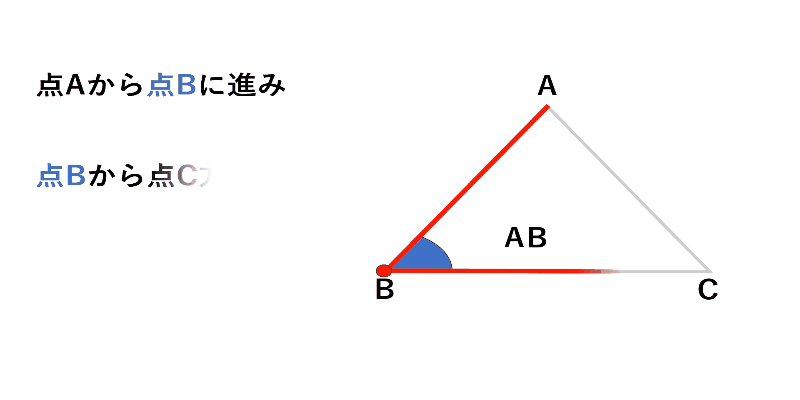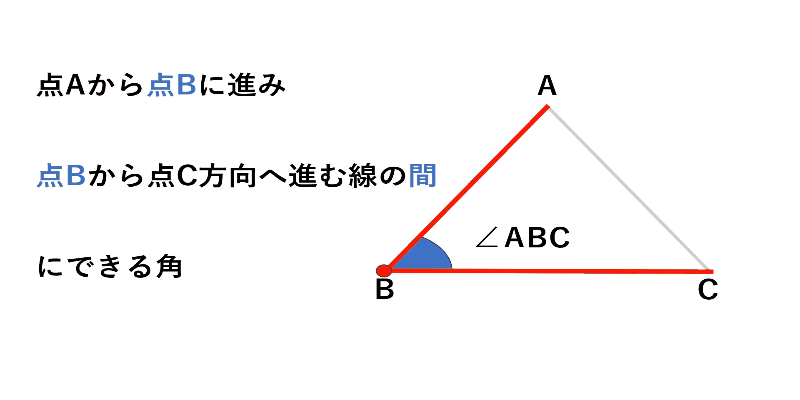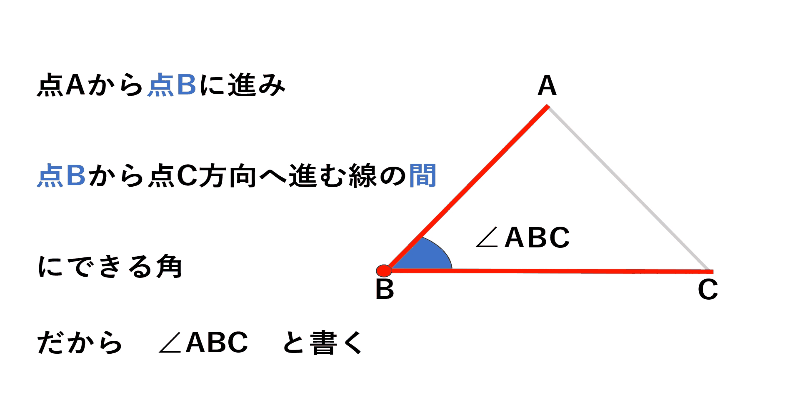
例えば次の図の$△ABC$で色を付けた角Bを表すときは、
$∠ABC$ とします。
$∠ABC$ のように、3つのアルファベットを使って角を表すことに初めのうちは慣れないと思いますが、$∠ABC$の書き方をするように習慣づけてください。
もし$∠ABC$が45°だとしたら
$∠ABC=45°$ と書きます。
また、$∠ABC$と$∠ACB$が同じ大きさだとしたら
$∠ABC=∠ACB$ と書きます。
表し方のイメージとして、
「点Aを出発して点Bを通って点Cへ向かう線の間にできる角」
だから、間にBを書くと考えると良いでしょう。
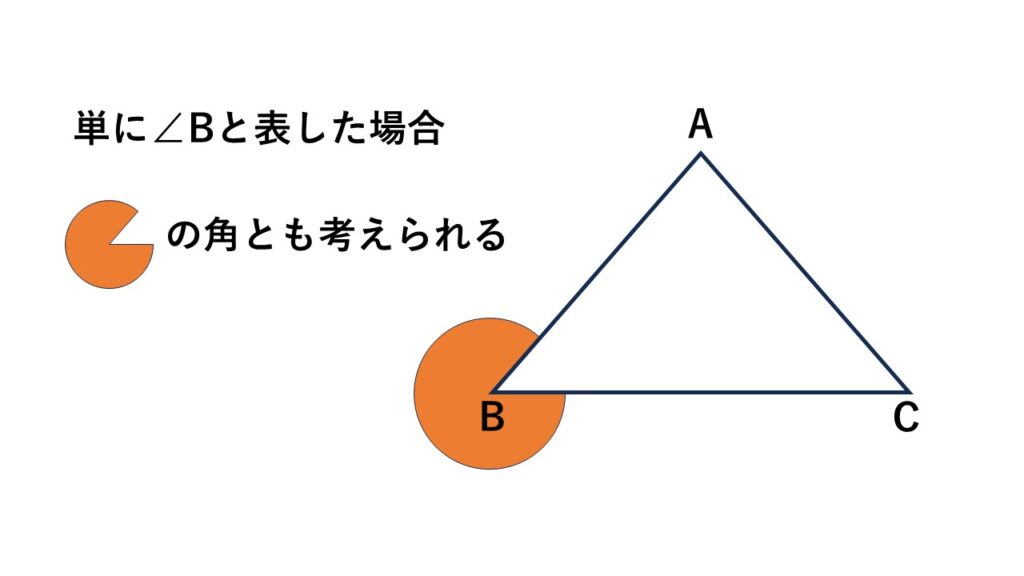
注意!!
$∠B$としても間違いとは言い切れないのですが、その場合どの角を示しているのかが不明確になることがあります。
$∠B$として表すときは、誤解が生じないように補足する必要があります。
直角と平行
2直線ABとCDが交わってできる角が90°（直角）のとき、直線ABとCDは垂直であるといい、
記号 ⊥ を使って$AB⊥CD$ と表します。
2直線EFとGHが交わらないとき、直線EFとGHは平行であるといい、
記号 // を使って$EF//GH$と表します。
点と直線の距離
点Pから直線$ℓ$に引いた垂線と、直線$ℓ$との交点を点Hとするとき、
線分PHの長さを点Pと直線$ℓ$との距離といいます。
垂線というところがポイント。単に点Pから直線$ℓ$に直線を引くだけなら無限に引けますが、垂線といったら1本に限定されます。
無限に引ける直線の中でも、垂線を引くときが一番長さが短くなります。その一番短い時を距離というわけです。
ここまでのことは表し方のルールなので、そういうこととして覚えてください。