平行四辺形については小学校でも学んでいますが、中学での内容はそこからさらに深入りして、どうしてそのような性質がいえるのかを説明できるようにしていきます。
まずは平行四辺形の性質を確認していきましょう。
平行四辺形の性質
平行四辺形の定義
2組の向かい合う辺がそれぞれ平行な四角形
日常的な言葉に翻訳すると、2組の向かい合う辺がそれぞれ平行な四角形のことを平行四辺形と呼ぶことにしましょう、となります。
ちなみに、
四角形$ABCD$で$AB//DC$ $AD//BC$
と表記されていたら、平行四辺形を意味しています。
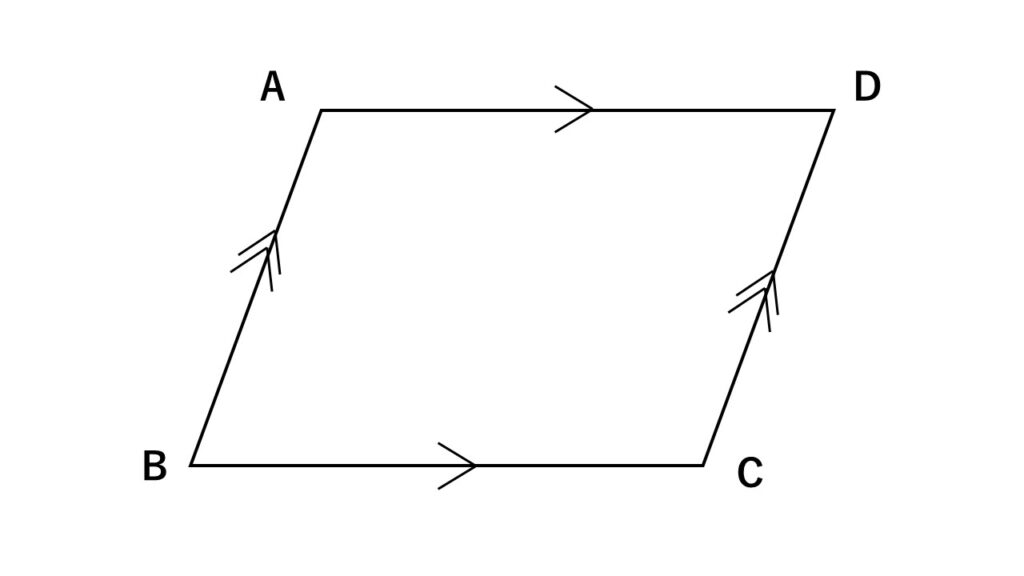
平行四辺形の性質 (定理)
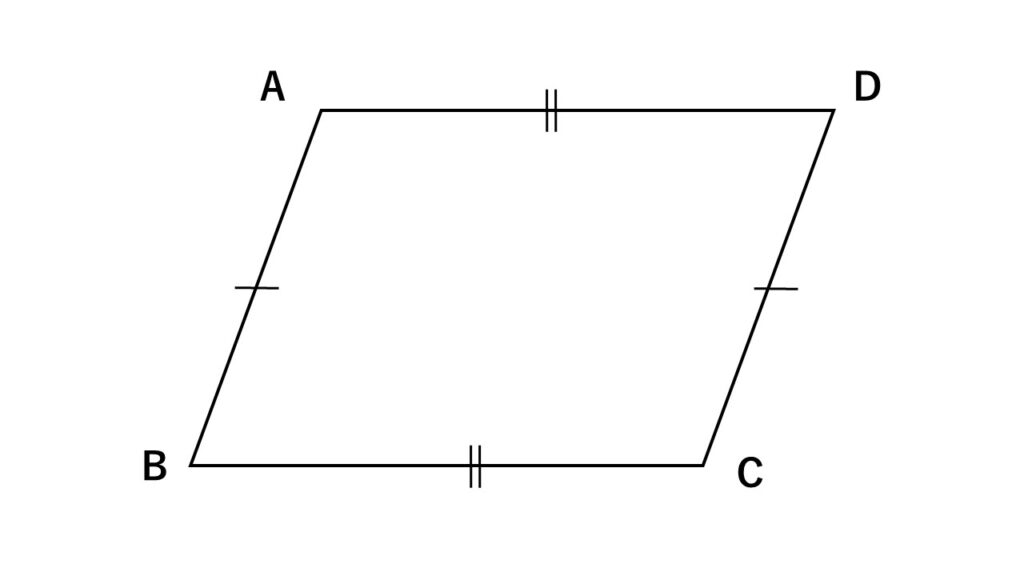
- 2組の対辺はそれぞれ等しい
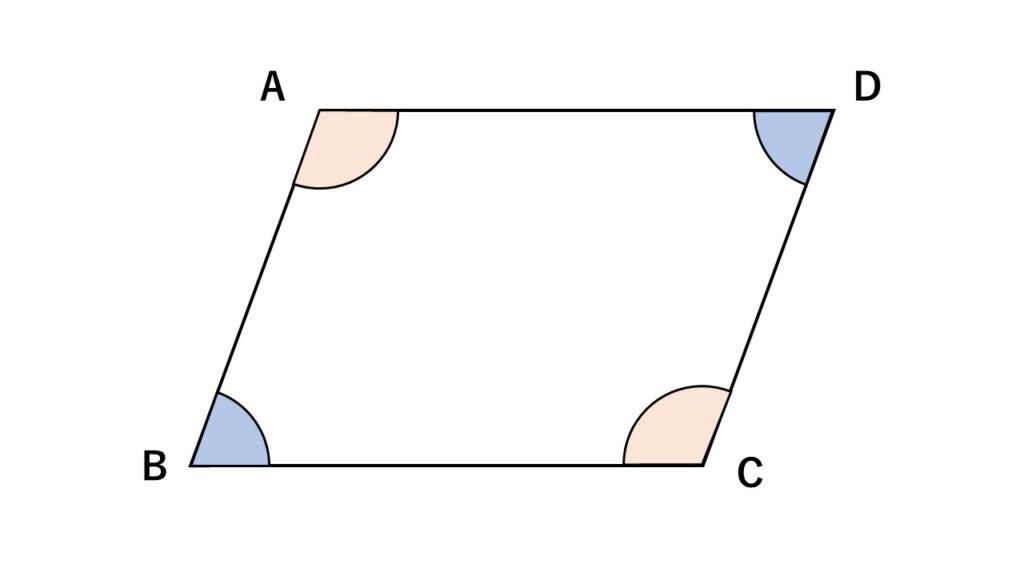
- 2組の対角はそれぞれ等しい
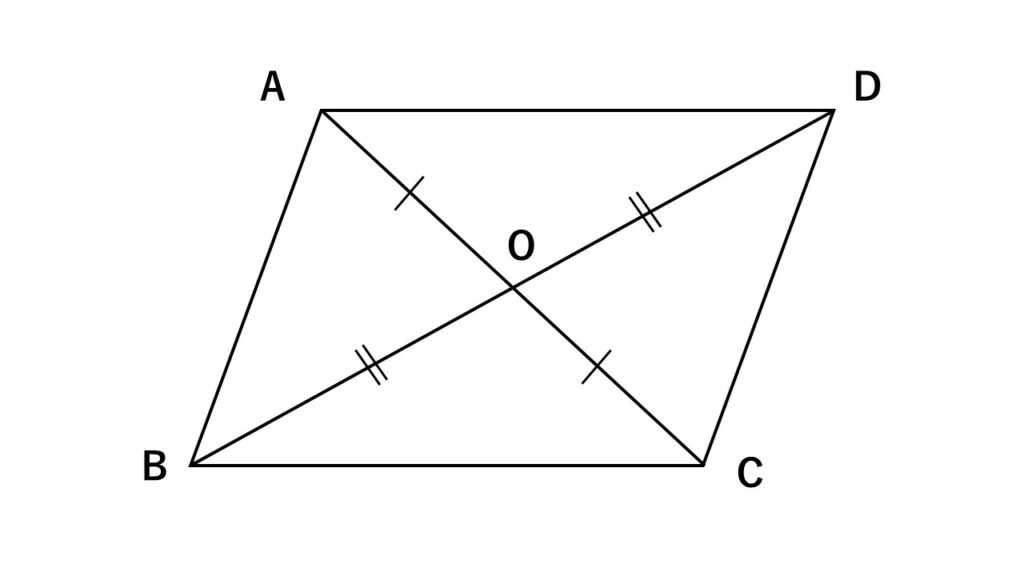
- 対角線はそれぞれの中点で交わる
まずはしっかり定義と定理を覚えてください。
次にどうして定理が成り立つのかを証明します。この証明も自力でできるようにしておきましょう。
平行四辺形の2組の対辺はそれぞれ等しいことの証明
証明
図のような平行四辺形$ABCD$で対角線$AC$を引く。
$\triangle ABC$と$\triangle CDA$において
平行四辺形の定義より
$AB//DC$ $BC//AD$
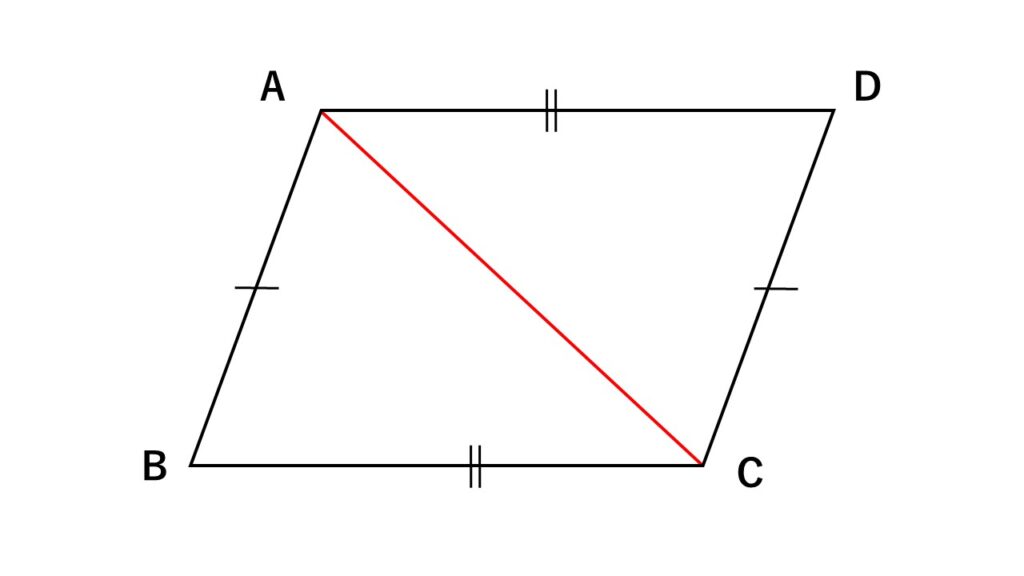
ここで平行線の錯角は等しいので
$\begin{align}\angle BAC&=\angle DCA&①\\\angle BCA&=\angle DAC&②\end{align}$
$AC$は共通 ③
①②③から1組の辺とその両端の角がそれぞれ等しいので
$\triangle ABC \equiv \triangle CDA$
合同な図形の対応する辺は等しいので
$AB=CD$ $BC=DC$
したがって平行四辺形の2組の対辺はそれぞれ等しいといえる
証明終わり
解説
この証明は
仮定:平行四辺形
結論:2組の対辺はそれぞれ等しい
なので、平行四辺形の定義(2組の向かい合う辺がそれぞれ平行)を証明の根拠として使えます。
つまり$AB//DC$ $BC//AD$を証明の過程で使えます。
すると平行線と錯角の関係から等しい角がわかり、三角形の合同条件を示せます。
合同といえれば対応する辺は等しいといえるので、結果として平行四辺形の2組の辺が等しい長さとなっていることが示せます。
平行四辺形に対角線を引いて三角形を作る所がポイントです。
次に平行四辺形の2組の対角はそれぞれ等しいことと対角線はそれぞれの中点で交わることの証明に移ります。
ただ$\triangle ABC \equiv \triangle CDA$までは上記証明と同じです。
よって合同より後の証明を続けて書きます。
平行四辺形の2組の対角はそれぞれ等しいことの証明
証明
$\triangle ABC \equiv \triangle CDA$より
合同な図形の対応する角は等しいので
$\angle ABC=\angle CDA$ ①
平行線の錯角は等しいので
$\begin{align}\angle BAC&=\angle DCA ②\\\angle BCA&=\angle DAC ③\end{align}$
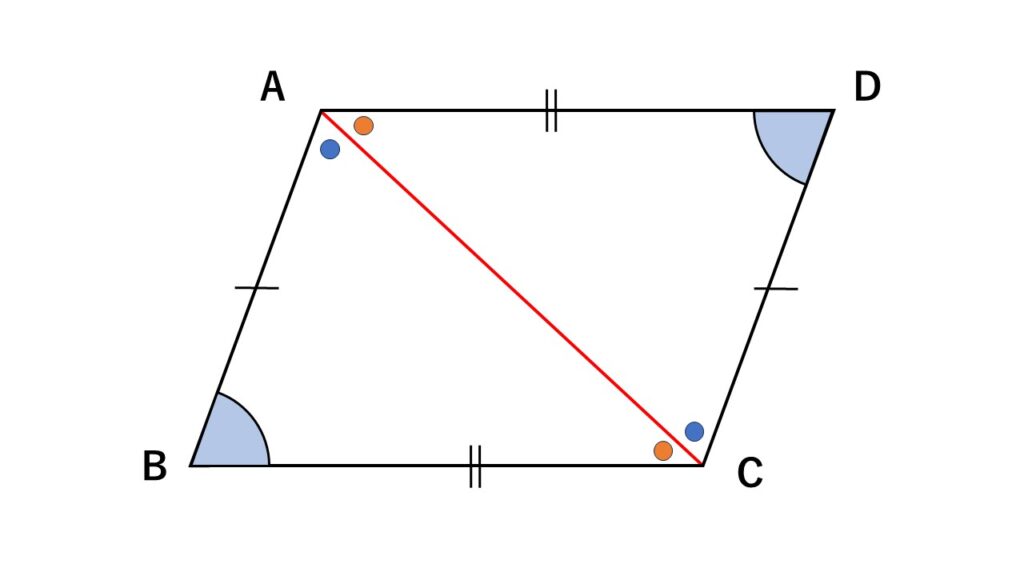
②③から
$\angle BAC+\angle DAC=\angle DCA+\angle BCA ④$
つまり$\angle BAD=\angle DCA$
したがって①④より
平行四辺形の2組の対角はそれぞれ等しいといえる
証明終わり
平行四辺形の対角線はそれぞれの中点で交わることの証明
この証明も$\triangle ABC \equiv \triangle CDA$を示し$\angle BCA=\angle DAC$までは上記と同じです。
そして合同なので$BC=DA$もいえます。
さらに平行線と錯角の関係から
$\angle ADB=\angle CBD$もいえます。
すると$\triangle AOD \equiv \triangle COB$がいえます。
ということで、$\triangle ABC \equiv \triangle CDA$を示したその続きから証明していきます。
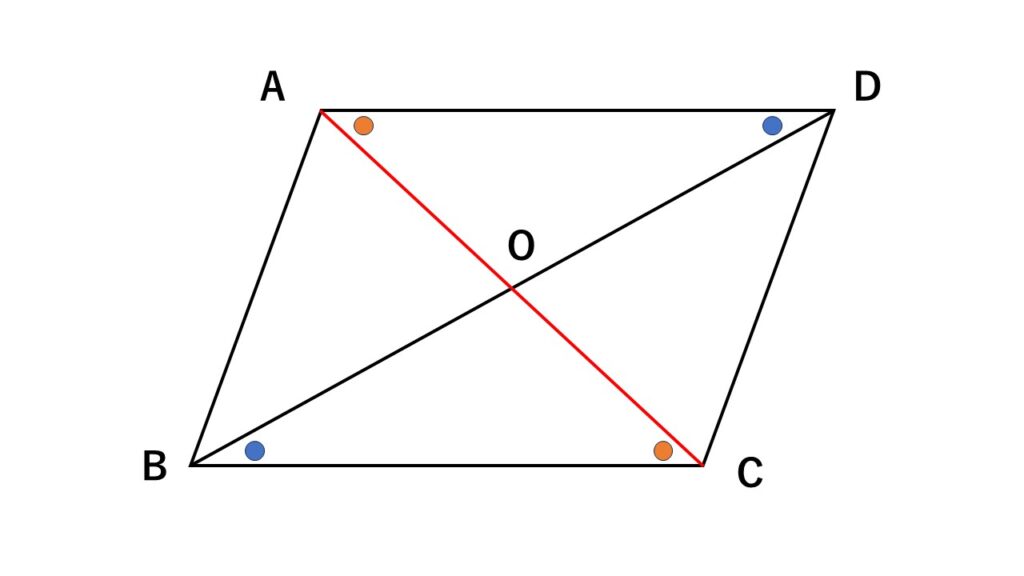
証明
$\triangle AOD$と$\triangle COB$において
$\triangle ABC \equiv \triangle CDA$より対応する辺は等しいので
$BC=DA ①$
さらに平行線と錯角の関係から
$\begin{align}\angle ADB&=\angle CBD&②\\\angle BCA&=\angle DAC&③\end{align}$
①②③より1組の辺とその両端の角がそれぞれ等しいので
$\triangle AOD\equiv \triangle COB$
これより対応する辺はそれぞれ等しいので
$BO=DO ④$
$AO=CO ⑤$
④⑤より平行四辺形の対角線はそれぞれの中点で交わるといえる
証明終わり
そもそも証明の根拠とは?
ここまで平行四辺形の性質を証明してきました。
平行四辺形の性質を証明しているから、当然平行四辺形の性質を証明の根拠にするわけにいきません。
この赤字の部分が何を言っているのかよくわからなければ、もう少し身近な次の具体例で考えてみてください。
『よしお君は撮り鉄くんであることを証明せよ』

さて、どうやって証明しますか?
「撮り鉄くんだから撮り鉄くんである」と言ったって何の説明にもなってないですよね。
よしお君が撮り鉄くんであることを証明するには、妙に鉄道ダイヤに詳しいとか、スマホの待ち受け画面がお茶の水の聖橋から秋葉原方面の風景になっている、神田川と聞くと真っ先に立体交差を思い浮かべてムズムズするなど、それなりの理由が複数必要です。

ダイヤの関係で中央線、総武線、丸ノ内線を1枚の写真に全て写すのは難しい
平行四辺形の性質を証明するのに平行四辺形の性質を根拠にしたら、撮り鉄くんだから撮り鉄くんであると同様に、何の説明にもなっていません。
そのため、
平行四辺形の性質を証明するならば、平行四辺形とは別の所から根拠を持ってくるようにします。
もし二等辺三角形の性質を証明するならば、二等辺三角形とは別の所から根拠を持ってきます。
もし直角三角形の性質を証明するならば、直角三角形とは別の所から根拠を持ってきます。
証明する際は根拠が重要です。
撮り鉄くんだから撮り鉄くんであるの論調にならないように十分注意しましょう。
平行四辺形の性質を使った練習問題
平行四辺形に話を戻します。
性質を証明するなら・・・と書いてきましたが、平行四辺形の問題を解くときは平行四辺形の性質をそのまま使って解いていきます。性質について証明する必要もありません。
平行四辺形に限らず図形問題では、証明問題でない限りその図形の性質をそのまま解答に使ってしまってかまいません。
ということで平行四辺形の性質を使って解く問題を練習しましょう。
基本例題
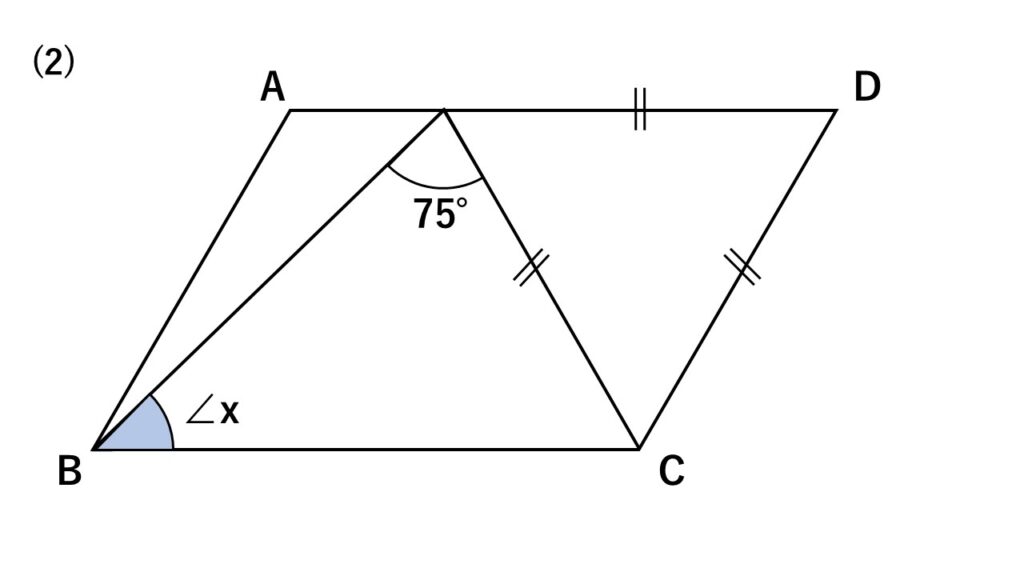
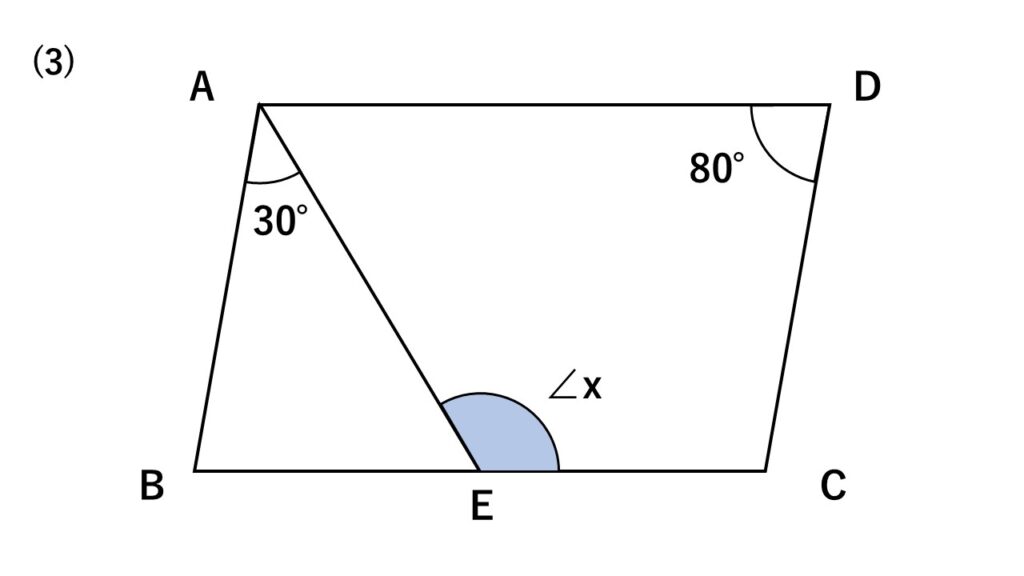
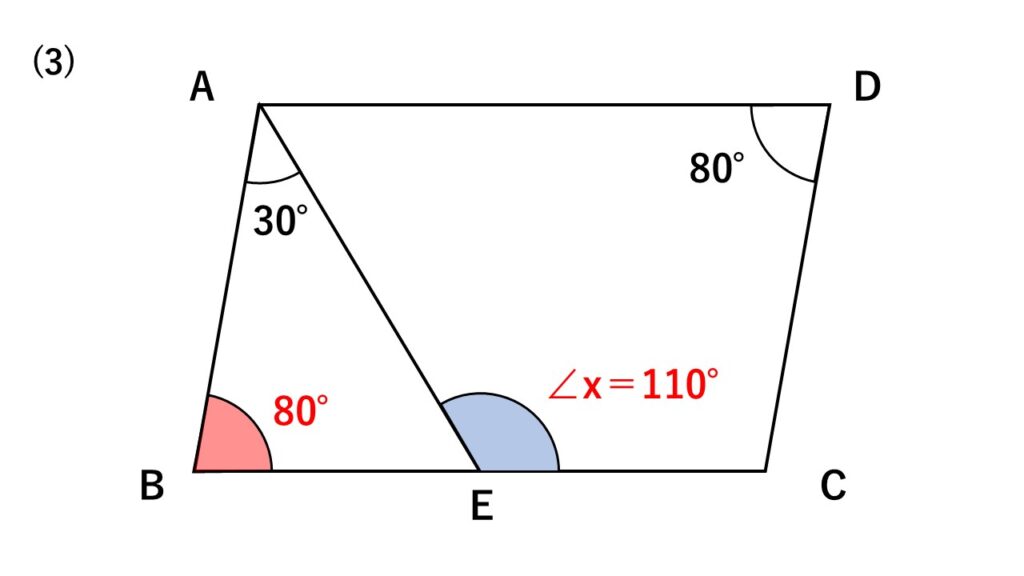
四角形$ABCD$は平行四辺形である。次の図の$\angle x$の大きさを求めよ。
なお、同じ印のものは同じ大きさを表しているものとする。
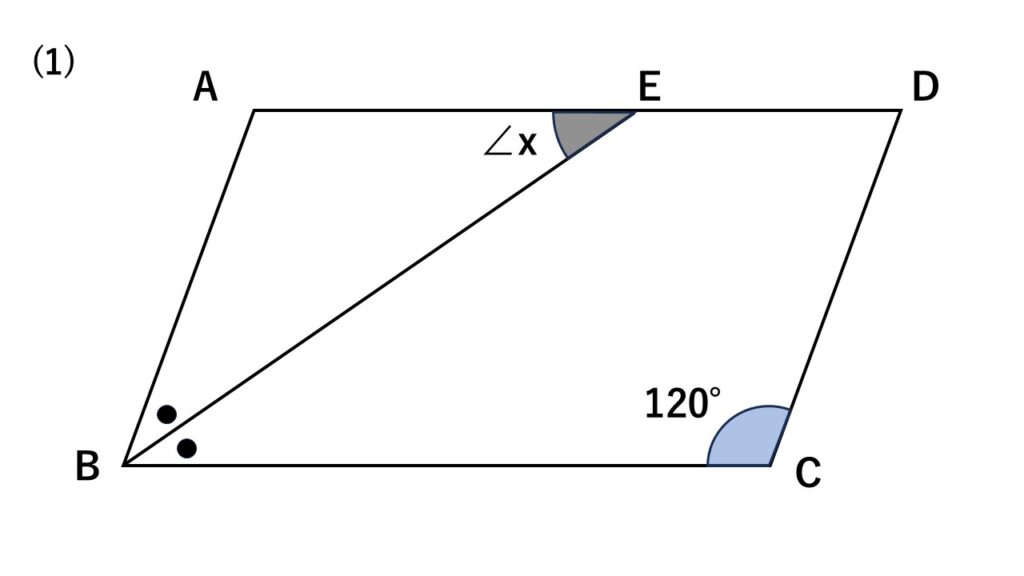
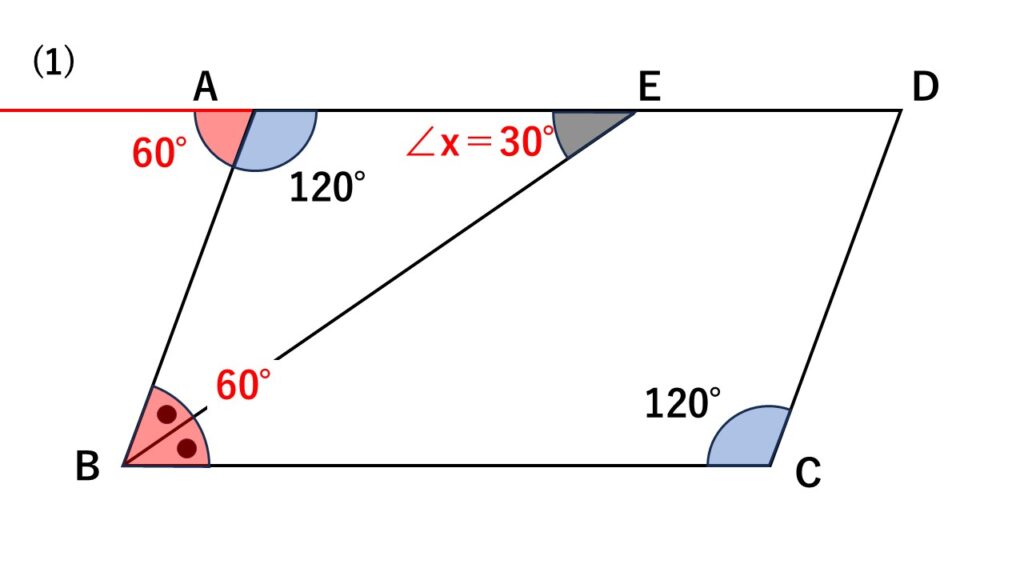
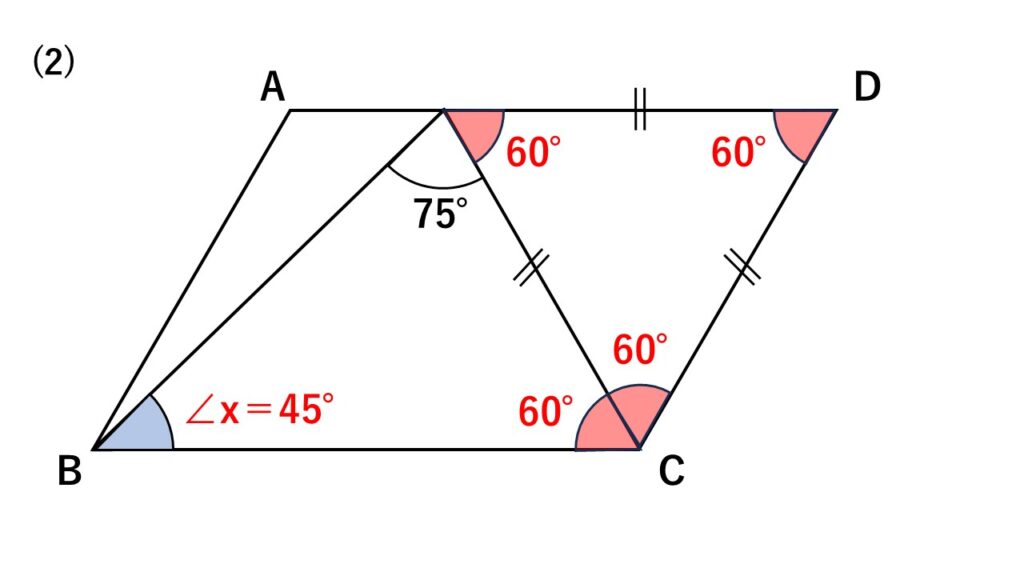
解答
平行四辺形の分類
2組の向かい合う辺がそれぞれ平行な四角形を平行四辺形と定義していますが、その定義に従うと長方形、ひし形、正方形も平行四辺形に分類されます。
平行四辺形の中でも特に、
4つの角が同じ大きさ、つまり90°であるものが長方形。
4つの辺が同じ長さになっているものがひし形。
その両方を満たしているものが正方形。
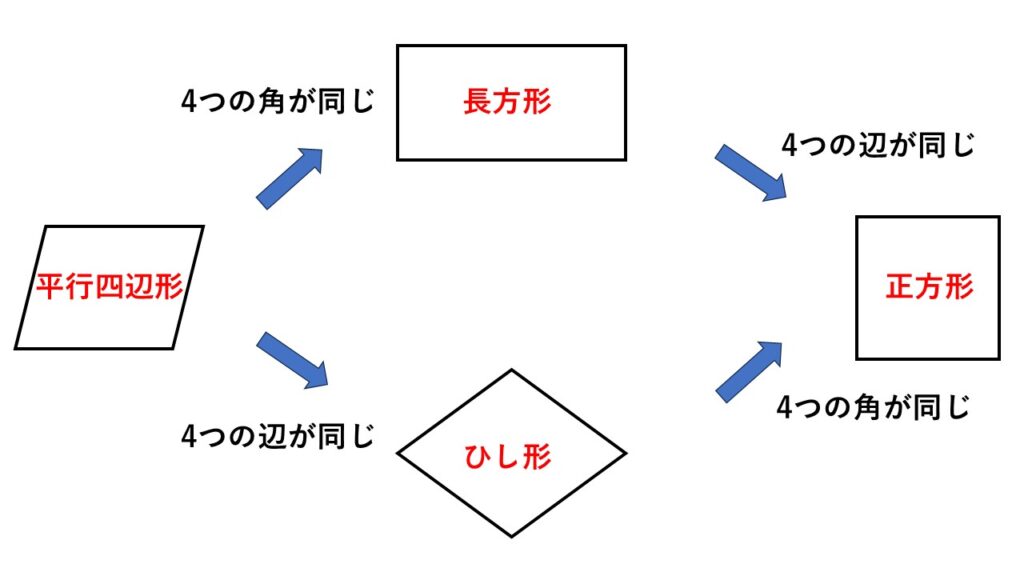
そのため長方形、ひし形、正方形それぞれ平行四辺形の性質がそのまま当てはまります。
