このページでは、どうして平行四辺形になるための条件を言えるとその四角形は平行四辺形だといえるのかを解説していきます。
平行四辺形になるための条件
平行四辺形になるための条件
その四角形が平行四辺形であることを証明する場合、平行四辺形になるための条件5つのうちのどれか1つを示していきます。
平行四辺形になるための条件
- 2組の対辺がそれぞれ平行である
- 2組の対辺がそれぞれ等しい
- 2組の対角がそれぞれ等しい
- 1組の対辺が平行でその長さが等しい
- 対角線がそれぞれの中点で交わる
平行四辺形になるための条件と言いつつ、内容は平行四辺形の性質と同じですね。
平行四辺形であることを示すために必要なこと
少々ややこしい話になるので初めに整理しておきます。
「平行四辺形だ!!」ということを証明するには、
平行四辺形の定義、つまり「2組の対辺がそれぞれ平行になっている」ことを示せば証明したことになります。
だってそうですよね?
「2組の対辺がそれぞれ平行な四角形のことを平行四辺形という」ことに決めてるわけですから。
ということで、「平行四辺形であることを証明するには2組の対辺がそれぞれ平行になっていることを示すのが基本」と覚えておいてください。
このことを踏まえて以下の証明を読み進めてください。
そして自力でも証明できるようにしておきましょう。
平行四辺形になるための条件が成り立つ理由
なぜ2組の対辺がそれぞれ平行であるならば平行四辺形なのか
上記の通り定義のことなので、これは証明も何もありません。
なぜ2組の対辺がそれぞれ等しいならば平行四辺形なのか
四角形$ABCD$について、
$AB=CD、AD=BC$ が条件になっています。
これをもとに
2組の対辺がそれぞれ平行である
つまり$AB//CD、AD//BC$
を示します。
もちろん$AB=CD、AD=BC$だけでは証明できないので、他に隠れた条件を見つけて証明していきます。そのために補助線を引きます。
ここでは対角線$AC$を引いて進めます。
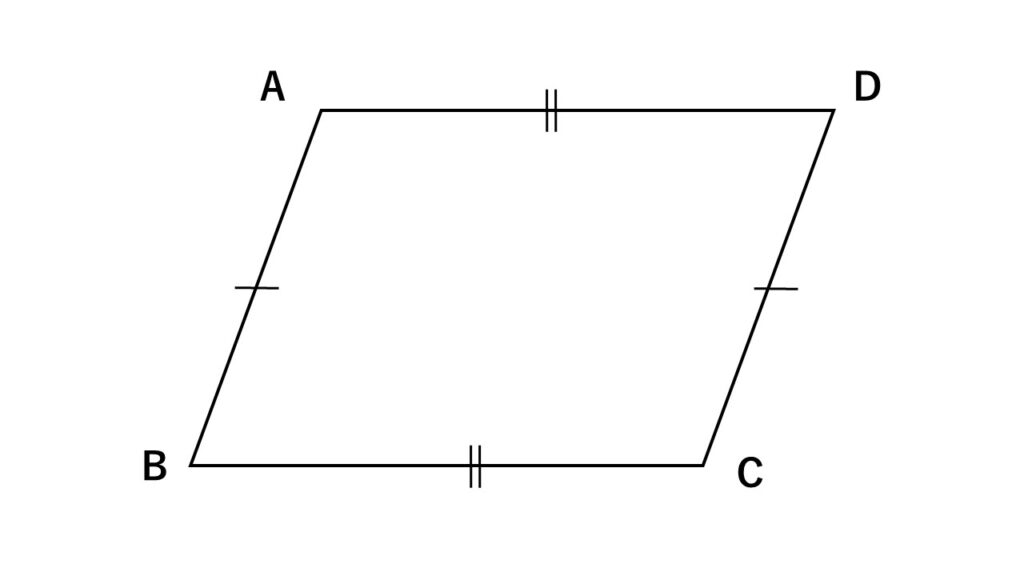
証明
四角形$ABCD$に対角線$AC$を引く
ここで$\triangle ABC$と$\triangle CDA$において
仮定より
$AB=CD$ ①
$BC=DA$ ②
対角線を引いたことより
$AC=CA$ ③
①②③より
3組の辺がそれぞれ等しいので
$\triangle ABC\equiv \triangle CDA$
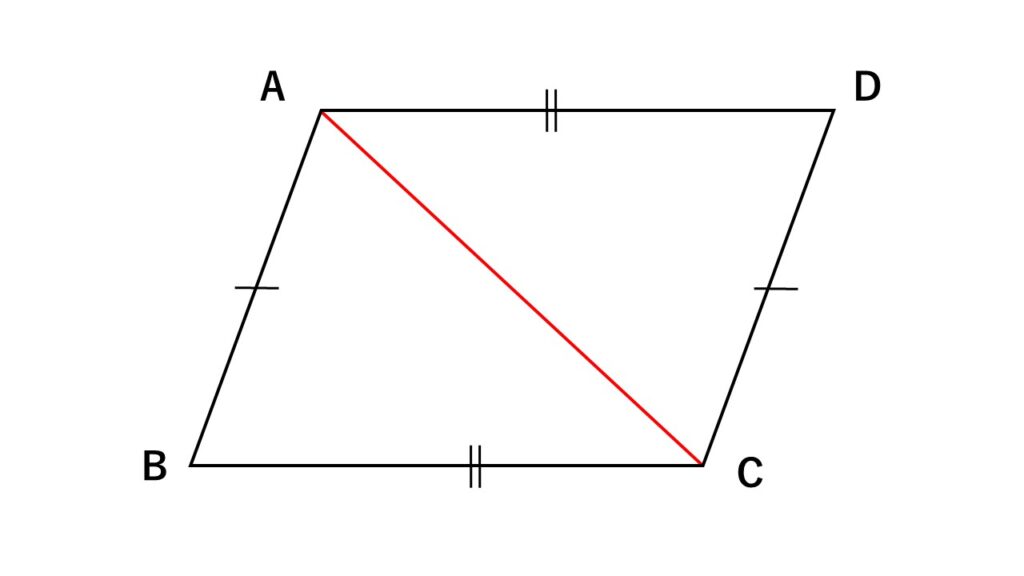
対応する角は等しいので
$\angle BAC=\angle DCA$
これより錯角が等しいので平行線と錯角の関係から
$AB//CD$ ④
同様に
$\angle BCA=\angle DAC$ より
$AD//BC$ ⑤
←角に関して説明しないと平行を示せないので、錯角に注目する
④⑤より2組の対辺がそれぞれ平行なので
四角形$ABCD$は平行四辺形である
したがって、四角形の2組の対辺がそれぞれ等しければ平行四辺形となる
証明終わり
←平行四辺形の定義で平行四辺形であることを示し、その結果として2組の対辺が等しいときに成り立つと結論づける
解説
重要なので繰り返しますが、
「2組の対辺が平行である」ことを示せば、その四角形は平行四辺形です。
そこで平行を示すために角度に注目します。しかし角度に関する手がかりがありません。
そのため対角線を引いて、半ば強引に角度を作りました。
これが隠れた条件を見つけるツボ。
すると錯角ができます。
錯角が等しければ2直線は平行であることに注目し、証明を進めています。
平行であることを示す方法として、
平行線と錯角の関係や、平行線と同位角の関係があります。
忘れていた人はこちらのページも合わせて確認しておきましょう。

平行であることを示すときは
平行線と錯角の関係 や
平行線と同位角の関係 を使う
なぜ2組の対角がそれぞれ等しいならば平行四辺形なのか
四角形$ABCD$について、
$\angle ABC=\angle CDA、\angle BAD=\angle DCB$ が条件になっています。
これをもとに
2組の対辺がそれぞれ平行である
つまり$AB//CD、AD//BC$
を示します。
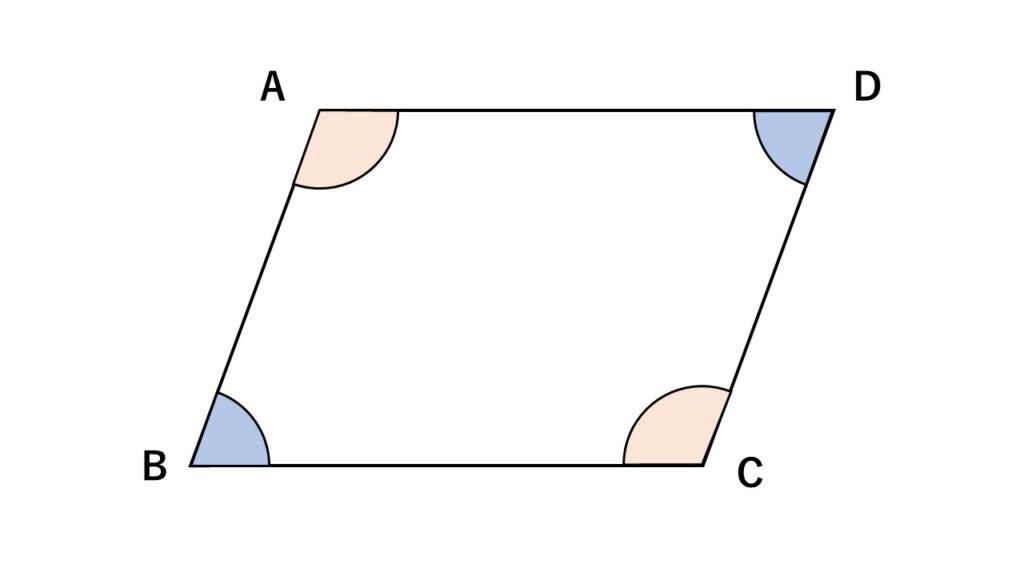
もちろん$\angle ABC=\angle CDA、\angle BAD=\angle DCB$だけでは証明できないので補助線を引きます。
ここでは$BC$を延長して進めます。
平行を示す鍵は角なので、平行線と錯角の関係だけでなく、四角形の内角の和にも注目していきます。
証明
四角形$ABCD$の辺$BC$を$C$方向へ延長し、その延長線上に点$E$を取る
すると直線は$180°$なので
$\angle BCE=180°$ ①
また仮定より
$\angle ABC=\angle CDA$ ②
$\angle BAD=\angle DCB$ ③

四角形の内角の和は$360°$なので②③と合わせて
$\begin{align}\angle BAD+\angle ABC+\angle DCB+\angle CDA&=360\\2\angle DCB+2\angle CDA&=360\end{align}$
したがって
$\angle DCB+\angle CDA=180$ ④
←平行線と錯角の関係を示すための準備段階
錯角が等しければ平行であることを示したい
ところで①より
$\angle BCE=\angle DCB+\angle DCE=180$ ⑤
ここで④と⑤を合わせると
$\angle DCB+\angle CDA=\angle DCB+\angle DCE=180$から
$\angle CDA=\angle DCE$ ⑥
これは錯角が等しいことを表している
したがって$AD//BC$ ⑦となる
←1組の対辺が平行であることを示した
もう1組の対辺も平行であることを示す
同様に考えて
$AB//BC$ ⑧
⑦⑧より2組の対辺がそれぞれ平行なので
四角形$ABCD$は平行四辺形となる
したがって
四角形の2組の対角がそれぞれ等しければ平行四辺形となる
証明終わり
←こちらが本来証明するべき結論
解説
角について色々書いたので証明が長くなりましたが、証明自体は単純。
錯角が等しいから平行になってるでしょ
↓
だから結果として2組の対角がそれぞれ等しければ平行四辺形になるじゃん
ということを説明しています。
錯角が等しいことを示すまでがこの証明の工夫のポイント。
証明そのものを丸暗記してテストで解答しようと考えると頭がパンクします。
必ず理屈を理解するようにしましょう。
なぜ1組の対辺が平行でその長さが等しいならば平行四辺形なのか
四角形$ABCD$について、
$AD//BC$ $AD=BC$が条件になっています。
これをもとに
2組の対辺がそれぞれ平行である
つまり$AB//CD、AD//BC$
を示します。
実質$AB//CD$をどうやって示すかです。
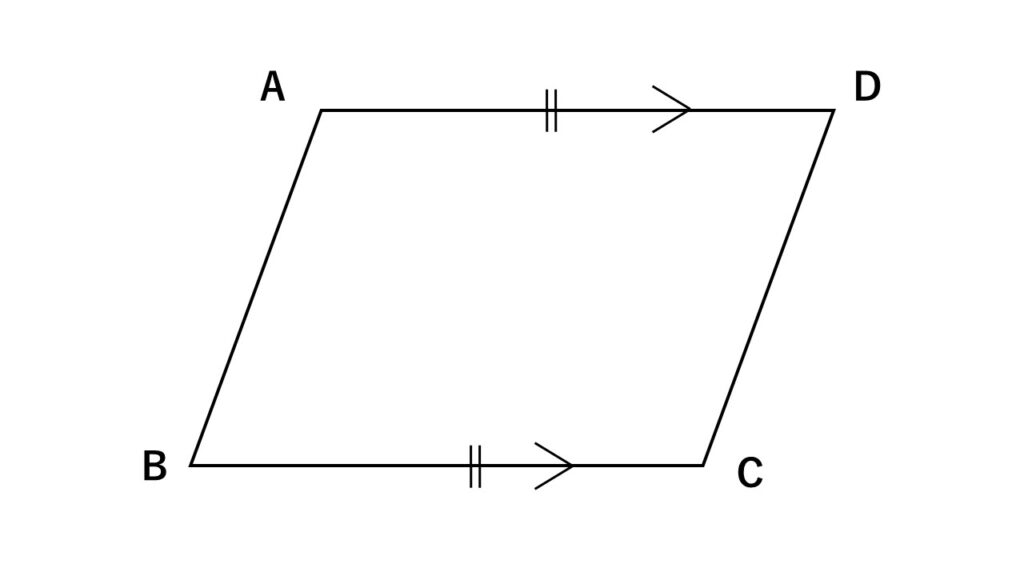
補助線を引いて平行線と錯角の関係に持っていくのは何となくわかってきたと思います。
ではどのような補助線を引くか?
$AB//CD$を示すために平行線と錯角の関係を使いたい。
すると四角形に対角線を引くと上手くいきそうです。
証明
四角形$ABCD$について対角線$AC$を引く
$\triangle ABC$と$\triangle CDA$において
仮定より
$BC=DA$ ①
対角線は共通なので
$AC=CA$ ②
平行線と錯角の関係から
$\angle ACB=\angle CAD$ ③
①②③より
2組の辺とその間の角がそれぞれ等しいので
$\triangle ABC\equiv \triangle CDA$
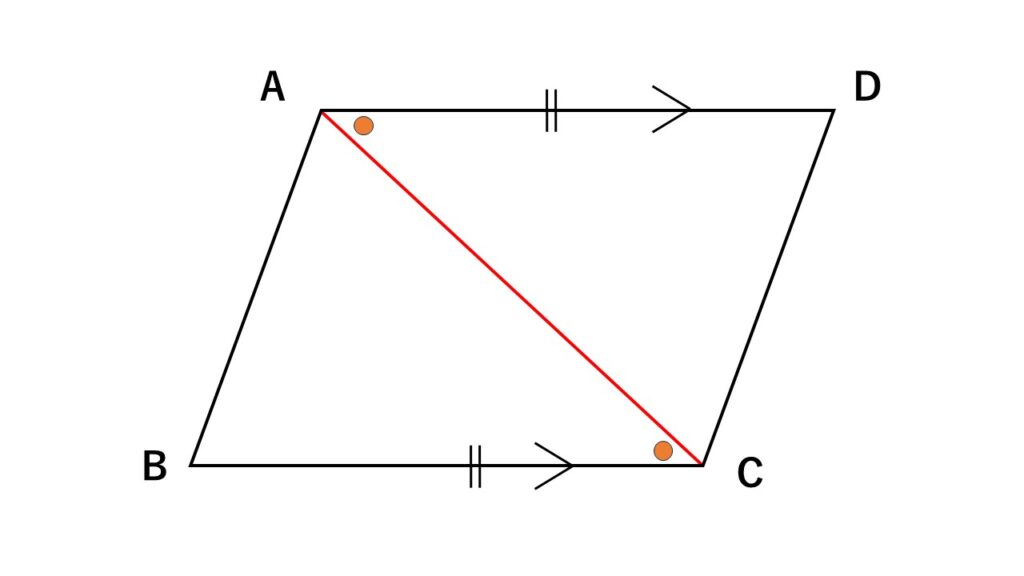
対応する角は等しいので
$\angle BAC=\angle DCA$
これは錯角なので平行線と錯角の関係から
$AB//CD$
よって$AD//BC$ $AB//CD$となり
四角形$ABCD$は平行四辺形となる
したがって
四角形の1組の辺が平行でその長さが等しければ平行四辺形となる
証明終わり
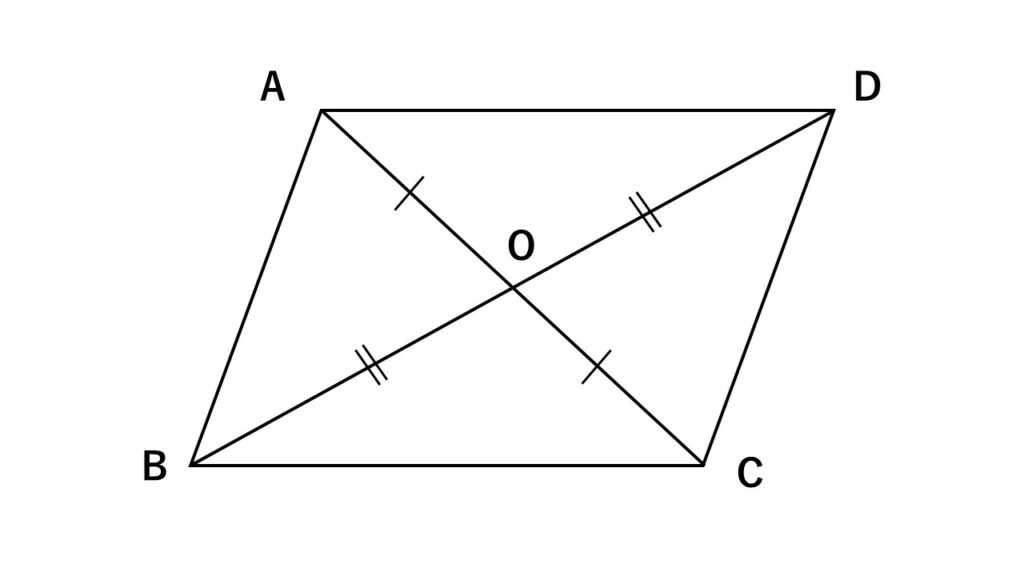
なぜ四角形の対角線がそれぞれの中点で交わるならば平行四辺形なのか
四角形$ABCD$について、
$AO=CO$ $BO=DO$が条件になっています。
これをもとに
2組の対辺がそれぞれ平行である
つまり$AB//CD、AD//BC$
を示します。
これは補助線を引かなくても証明できます。
三角形の合同を示す
↓
対応する角は等しいことを示す
↓
平行線と錯角の関係を示す
↓
2組の対辺が平行になっている
の流れで進めます。
証明
四角形$ABCD$の2つの対角線の交点を$O$とする
$\triangle OAB$と$\triangle OCD$において
仮定より
$OA=OC$ ①
$OB=OD$ ②
対頂角は等しいので
$\angle AOB=\angle COD$ ③
①②③より2組の辺とその間の角がそれぞれ等しいので
$\triangle OAB\equiv \triangle OCD$
対応する角は等しいので
$\angle OAB=\angle OCD$ ④
$\angle OBA=\angle ODC$ ⑤
④⑤はそれぞれ錯角の関係にあるので
$AB//CD$ ⑥
また同様に$\triangle OAD\equiv\triangle OCB$なので
$\angle OAD=\angle OCB$となり$AD//BC$ ⑦
⑥⑦より
2組の対辺がそれぞれ平行なので四角形$ABCD$は平行四辺形となる
したがって四角形の対角線がそれぞれの中点で交わるならば平行四辺形となる
証明終わり
平行四辺形になることを証明するには定義に行きつくことを示す
ここでもう一度頭の中を整理しておきましょう。
冒頭にも書いた通り、平行四辺形であることを証明するには定義である「2組の対辺がそれぞれ平行」であることを示すのが基本です。
でも、こう書くと次のように疑問を持った人もいるでしょう。
「平行四辺形であることを示すには平行四辺形になるための条件を示すって学校で教わったぞ!! でも定義を示すのが基本っておかしいだろっ。じゃぁせっかく覚えた平行四辺形になるための条件って何なんだよ、あぁ?」と。

そう、その疑問はごもっともです。
確かに平行四辺形であることを示すには平行四辺形になるための条件を示して証明します。
と、ここで頭を整理してほしいのが、このページで紹介してきた証明は全て「結論が平行四辺形の定義に行きついている」ということ。
つまり、
本来は定義を示すことで平行四辺形であることを証明していくけれど、平行四辺形になるための条件5つは結果的に定義に行きつくから、平行四辺形になるための条件を示してもOKですよ。
というわけです。
そのため今後テストで「平行四辺形であることを証明せよ」と出題されたら、平行四辺形になるための条件を示す形で証明を進めていきます。
ただ注意してほしいのが、
平行四辺形になるための条件を証明(このページでやってきたこと)するときには、
平行四辺形になるための条件を使わないで証明しなければなりません。
だってそうですよね?
平行四辺形になるための条件を証明するのに、その根拠を平行四辺形になるための条件にしては説明にならないわけですから。
証明を進める際は何を根拠にするか、そして根拠の繰り返しになっていないかを見極めることが大切です。

