三角形の相似から少し発展させて考えると、平行線と線分の比の関係が解ってきます。
「平行線と線分の比」
字面を見ると何やら小難しそうですが、理屈が分かれば実は簡単な内容です。
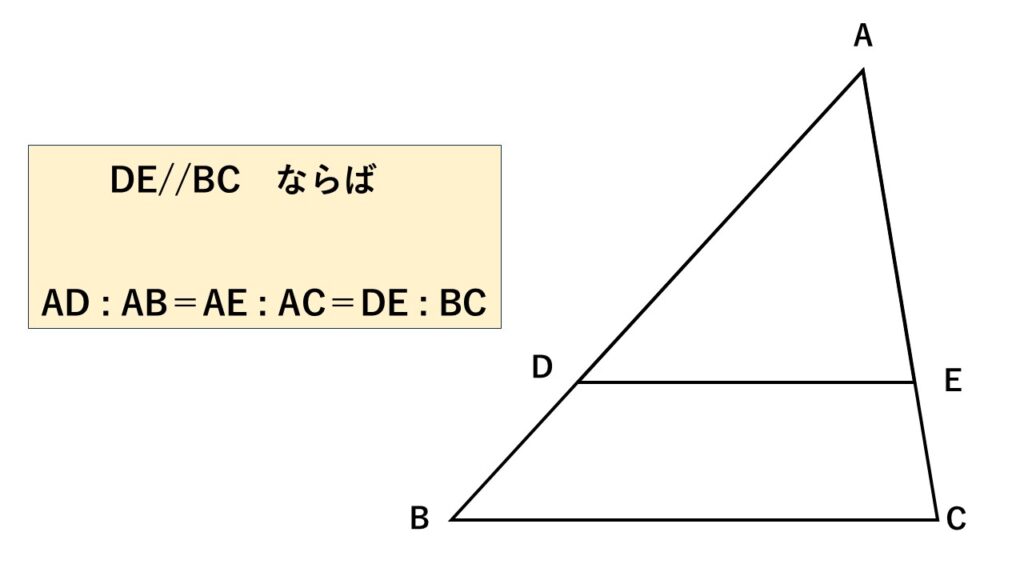
平行線と線分の比1 $AD:AB＝AE:AC＝DE:BC$ とは？
図のように$\triangle ABC$があり、
その中に$BC$と平行な線分$DE$を引くと
$AD:AB=AE:AC=DE:BC$
の関係が成り立ちます。
この関係は、$\triangle ABC\backsim\triangle ADE$から説明できます。
このページは相似の証明がメインではないので簡単に記します。
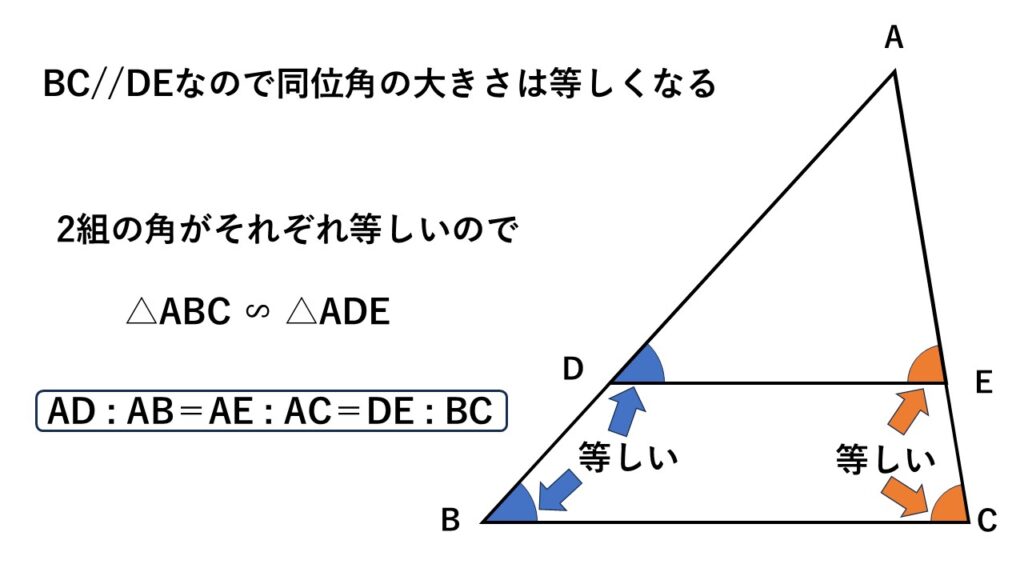
平行線と同位角の関係から図の同じ色の角は同じ大きさになります。
すると2組の角がそれぞれ等しいので
$\triangle ABC\backsim\triangle ADE$
よって対応する辺の比は等しいので
$AD:AB=AE:AC=DE:BC$
が成り立つわけです。
アルファベットの並びだけを見るとどうにも強烈な内容に感じますが、
相似な三角形を1つに組み合わせて対応する辺の比を示しただけです。
そう考えると何ら難しくないですよね。
平行線と線分の比についてはこの関係が基本になります。
そして平行線と線分の比について、他にも覚えておきたい関係があります。それが次。
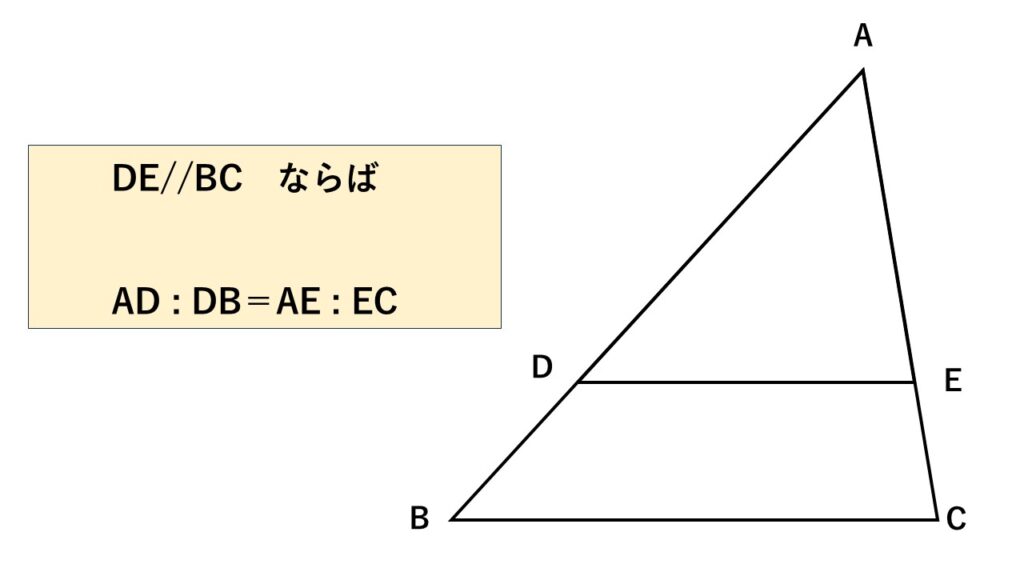
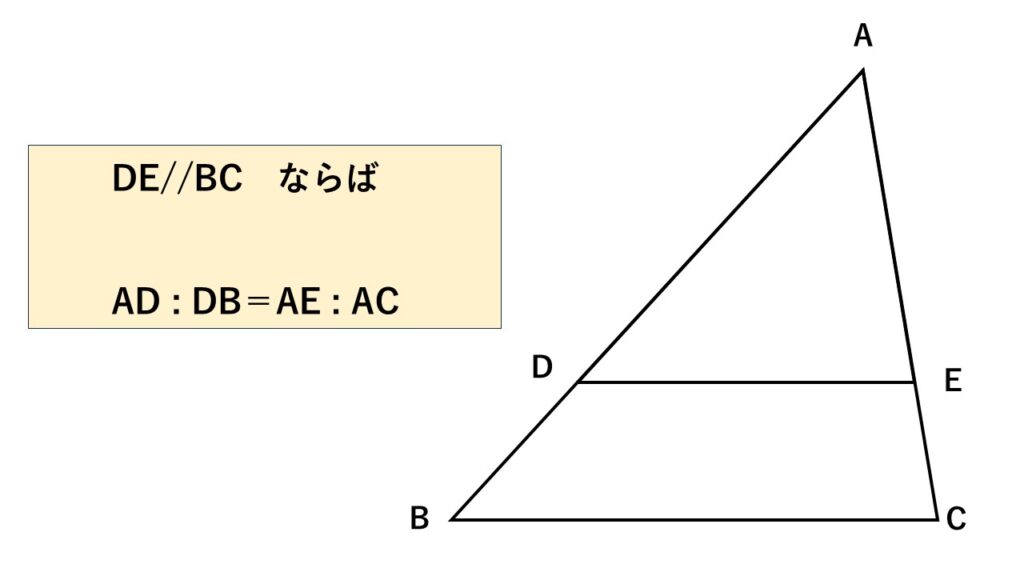
平行線と線分の比2 $AD:DB=AE:EC$ とは？
図のように$\triangle ABC$があり、
その中に$BC$と平行な線分$DE$を引くと
$AD:DB=AE:EC$
の関係が成り立ちます。
この関係の説明にはちょっとした工夫が必要です。
その工夫とは
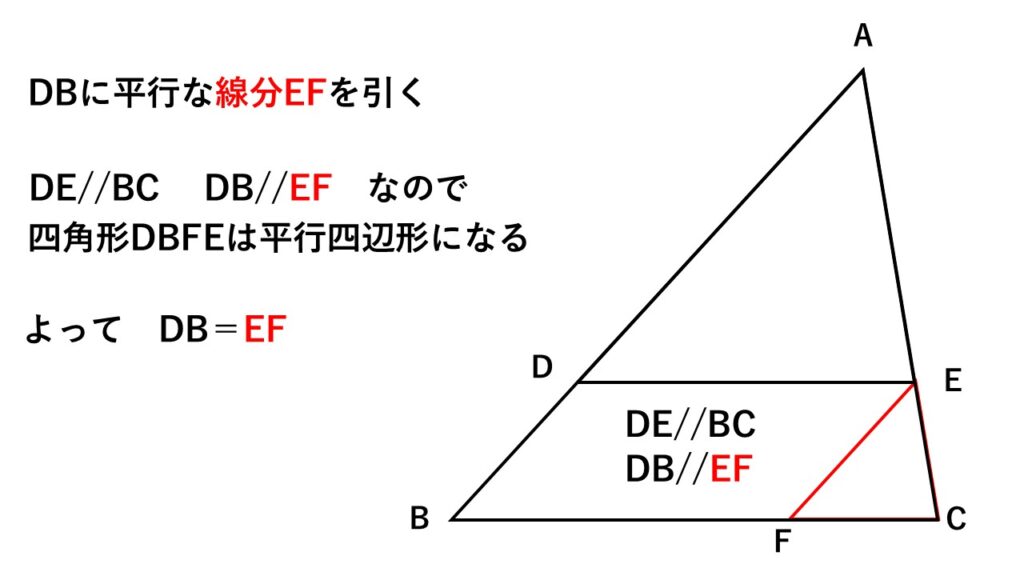
$DB$に平行な線分$EF$を引くこと。
すると平行四辺形ができます。
（2組の対辺がそれぞれ平行であるため）
この平行四辺形をフル活用します。
$DB=EF$であることに着目。
さらに線分$EF$を引いたことで
$\triangle EFC$ ができました。
すると平行線と同位角の関係から2組の角がそれぞれ等しいので
$\triangle ADE\backsim\triangle EFC$
対応する辺の比は等しいので
$AD:EF=AE:EC$
さらに $DB=EF$ なので
$AD:EF=AD:DB$ といえます。
よって
$AD:DB=AE:EC$
が成り立つわけです。
$DB$に平行な線分$EF$を引くことに気づけないと説明が先に進めないので、まぁ難しいといえば難しいですね。
ひとまずポイントは紹介したので、次の平行線と線分の比3に進みましょう。
なお、$DB$に平行な線分$EF$を引くことに疑問を持った人もいると思います。
そのあたり、もう少し深く理解したい人は以下を読んでみてください。
どうして平行な線分を引こうと考えたのか
ではどうして$DB$に平行な線分$EF$を引こうと考えたのか？
それは単純に図のままでは説明が進まないからです。
ここで相似の証明のページで強調した「逆算思考」をしていきます。
頭の中では次のように逆算します（しました）。
～頭の中～
$AD:DB=AE:EC$を示したい
↓
説明するにあたり$DB$の扱いが厄介
↓
$DB$に関する手がかりが欲しいが何も無い!! 困った
↓
無いから強引に作り出してしまえ!!
↓
とりあえず$DB$に平行な線をどっかに引いてみよう
↓
あ、$EF$を引いたら平行四辺形と相似な三角形ができた
↓
これらを使えば説明できるんじゃねぇ？？
この流れで$EF$を引けたわけです。
いいですか、教科書や参考書など紙面で証明問題を見ると簡単そうに、何事もなかったように線を引いて説明していますよね？
学校の先生や塾の先生が説明するときなんかは、いかにも得意げな何だかよくわからないけど勝ち誇ったかのような表情で、線を引いて説明してきます。
若干カチンと来ます。
で、この複雑・難しいことをいとも簡単に演じるから、中学生にとってはビビッてしまうわけです。
でもこれ、青字で強調したように逆算思考したことによる試行錯誤の結果です。
別に、最初から分かっていたわけでもなければ、反射的に閃いたものでもなく、考えに考えに考え抜いてようやく見つけた説明方法です。
何だか勝ち誇ってる表情の先生も、生徒が見てない所で必死こいて考えてます。
妙に勝ち誇った表情のときは、実は自信がなかった時の裏返しの可能性も･･･。
そんなときは先生を適当におだててすぐさま、
「どうしてその解き方を思いついたのか詳しく理由を教えてください!!」
とたたみかけましょう。君自身の熱心さをアピールできるとともに、先生に一泡吹かせることも期待できます。
とまぁそんなことはどうでもいいですが、とにかく色々試していることは確かです。
で、
どうして$BD$に平行な線を引こうと考えられたのか！？
例えば次の三角形の図。
まっすぐな線を1本だけ自由に引くとしたら、どこにどう引きますか？
あるいはもう少し限定して、平行線を引くとすればどこに引きますか？
真っ先に無意識的に思いついた線はどんなものでしょう？
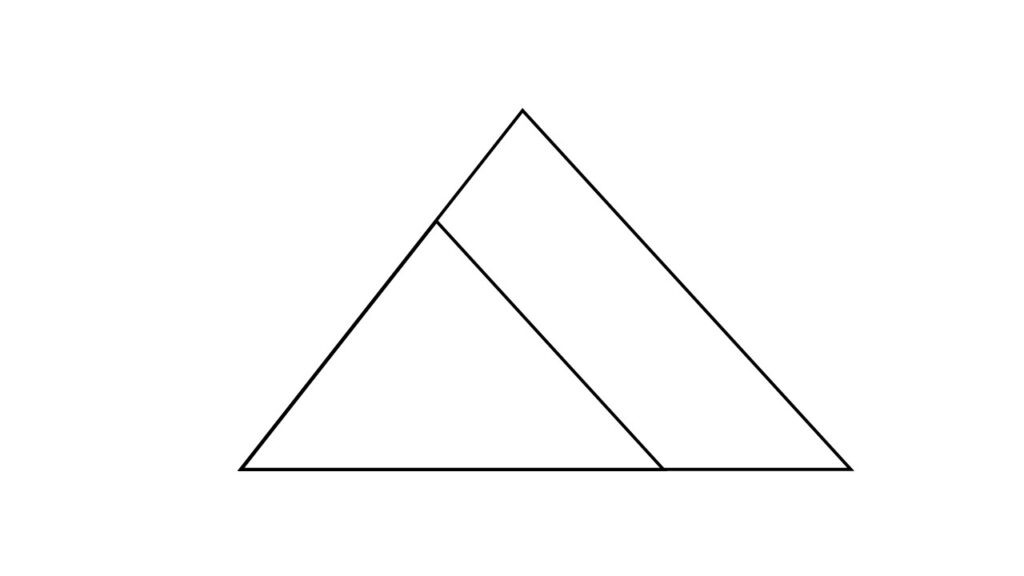
といわれると、
おそらく多くの人は底辺に平行な線を引くと思います。（もちろん縦線や斜めの線を引いた人もいるでしょう）
では「なぜその線を思いついたのか、その理由」は言えますか？
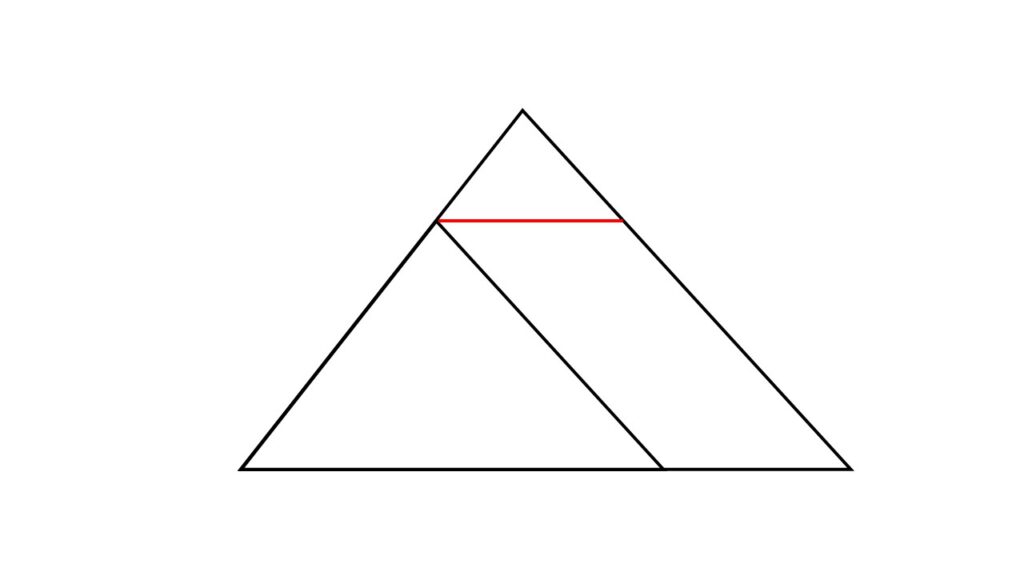
と、理由を問われると「なんとなく」とか、自分でも答えに困ってしまうのが正直なところだと思います。
要するに理由はないと。
そう、理由なんてどうでもいいんです。
とりあえず線を引いて、それがたまたまその線だったってことで良いんです。
ここで改めて
$AD:DB=AE:AC$
の証明に戻ります。
どうして$DB$に平行な線$EF$を引こうと考えられたのか？
もうわかりますよね？ たまたまうまくいったってだけのことです。
ただ、
ヒトは、縦や横方向のものについてはイメージしやすい傾向がありそうです。
逆に$19.2$°といった斜め方向については縦横ほどではないようです。
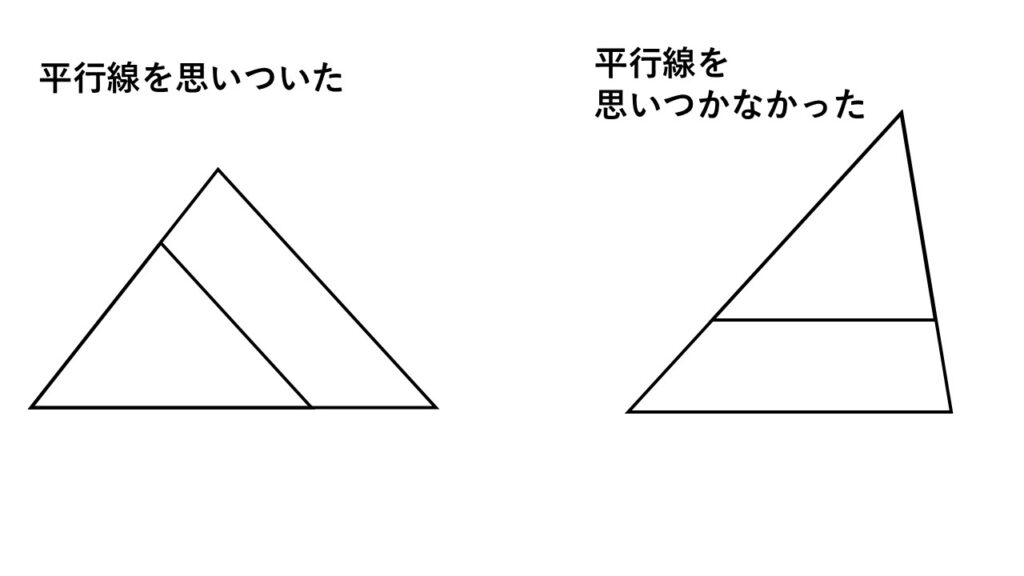
どうして$BD$に平行な線$EF$を引こうと考えられたのか!?
思いつかなかった人や難しく感じる人は、斜めの罠にハマったのかもしれません。
なお、補助線を引くときにはちょっとしたコツのようなものはあります。
こちらのページも参考に、補助線を引くときの目のつけ所も確認してみてください。
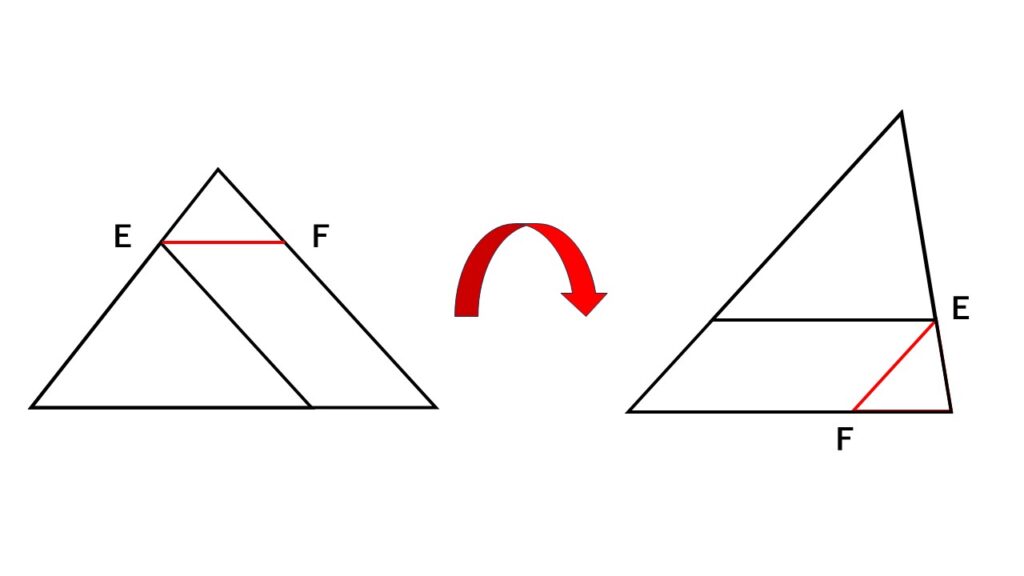
平行線と線分の比にはまだ覚えておきたい関係があります。
それが次。
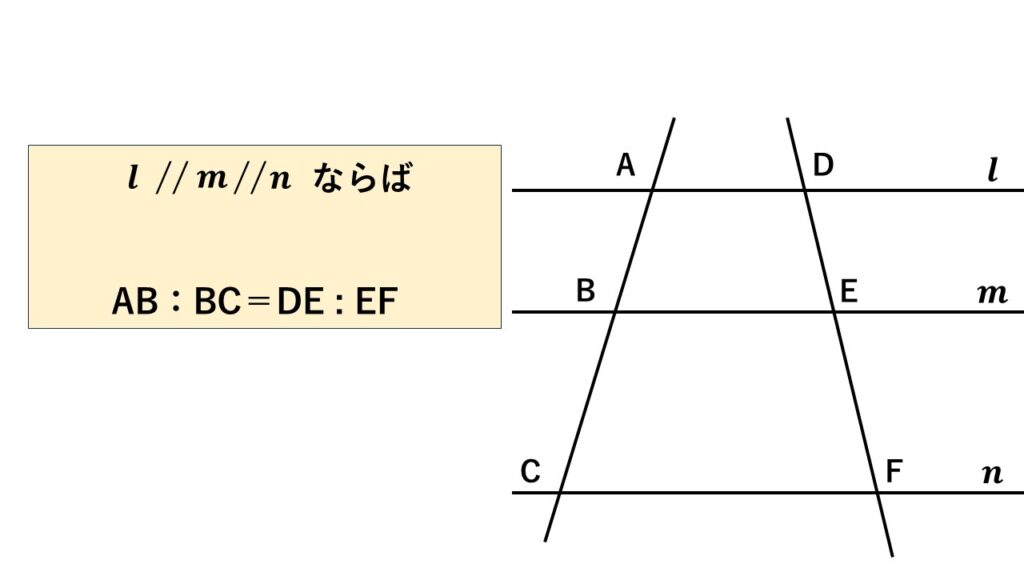
平行線と線分の比3 $AB:BC=DE:EF$ とは？
図のように直線$l,m,n$がそれぞれ平行で、そこに2本の直線が交わるとき
$AB:BC=DE:EF$
の関係が成り立ちます。
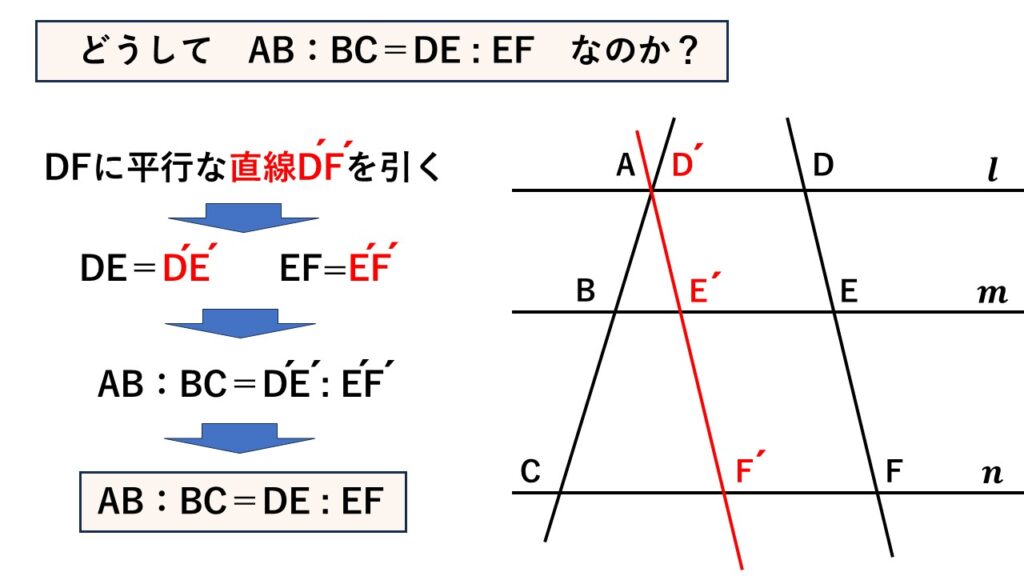
これは平行線と線分の比2から説明できます。
直線$DF$に平行な直線$D´F´$を、$A$と交わるように引きます。
すると$D´E´ED$は平行四辺形になるので、
$DE=D´E´$となります。
同様に$EF=E´F´$です。
あとは平行線と線分の比2で説明できます。
補助線を引けば簡単に理解できると思います。
ここまで平行線と線分の比について3つ紹介しました。
一度覚えてしまえば内容自体は簡単です。
おそらく平行線と線分の比として、単体の問題であれば難なく解答できると思います。
ただ他の図と組み合わさっての出題となると、途端に難しく感じてしまうのが平行線と線分の比。
そのため入試で問われやすい内容でもあります。要注意!!
教科書の例題や問いなどの基本問題を何回も繰り返し練習して、
「平行線を見たら線分の比を半ば反射的に思い出せる」
くらいにしておきましょう。