
分母が$0$の分数は定義されません。
いきなりポイントを書きましたが、定義とは約束事の意味。
つまり「分母が$0$の分数はこの世には存在しないものと決めましょう」ということです。
なぜ分母が$0$の分数は存在しないのかを説明すると本題から大きくそれるので割愛しますが、ざっくり言うと「0個に分けることは理屈上できないから」です。
このことを頭の片隅に置いて本題に入ります。
反比例のグラフの形
反比例$y=\dfrac{a}{x}$のグラフの形は、比例定数$a$が正の値か負の値かで変わってきます。
まずはざっくりで良いので反比例のグラフの形と特徴をおさえておきましょう。


反比例のグラフの特徴
①曲線になっている
②曲線が2つある(双曲線という)
③比例定数が正のときは第一象限と第三象限に、負のときは第二象限と第四象限に双曲線ができる
④双曲線は$x$軸や$y$軸に触れることはない
⑤双曲線は互いに交わることがない
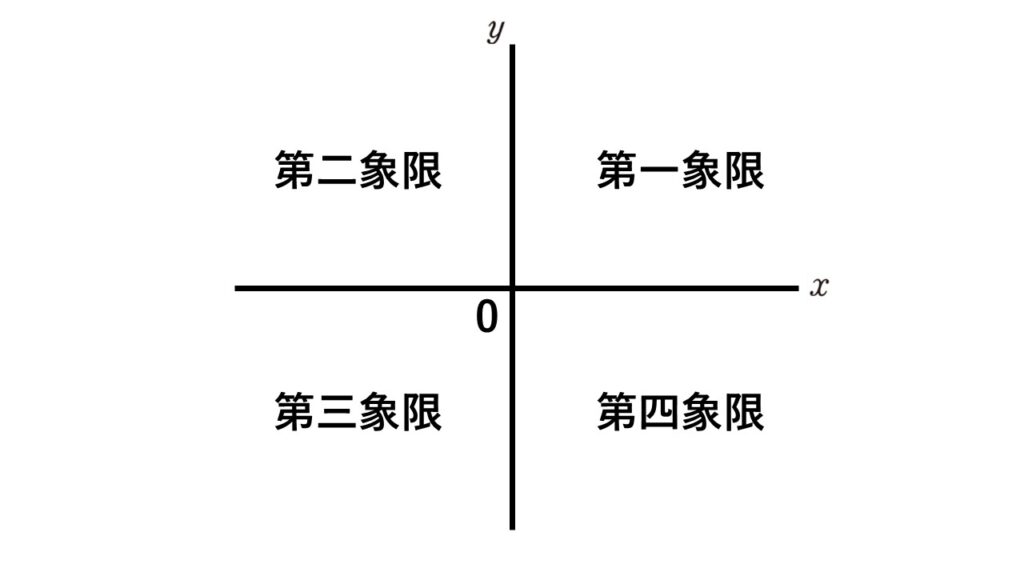
座標平面を$x$軸と$y$軸で区切ると4つの領域ができます。
その領域を右上から順に反時計回りに
第一象限、第二象限、第三象限、第四象限
とそれぞれいいます。
「反比例のグラフの特徴④双曲線は$x$軸や$y$軸に触れることはない」と書きましたが、その理由が冒頭に挙げたPOINT 「分母が$0$の分数は定義されません」にあります。
$y=\dfrac{a}{x}$において分母が0、つまり$x=0$というのは考えてはいけません。想像もしてはいけません。$x=0$ということ自体が存在しないのです。
このことを座標平面上で考えると、$y$軸上には何も存在しないということになります。
$y$軸上に何も存在しないのだから、$y$軸上にグラフが通るということ自体が起こりえない。だから「双曲線は$x$軸や$y$軸に触れることはない」となるわけです。
それに伴い、「⑤双曲線は互いに交わることがない」ことにもなってきます。
反比例のグラフのかき方
反比例のグラフは次の手順でかきます。

反比例のグラフをかく手順
①グラフが通る点の座標を10か所位求める
②求めた座標を曲線になるように結ぶ
反比例のグラフは曲線なので定規を使ってかくことはできません。フリーハンドでかきます。
なのでグラフとして歪な形になってしまうのは仕方ありません。
テストで反比例のグラフをかく出題をされたら、なるべく曲線としてかいた努力をしているように仕上げましょう。
では実際に反比例のグラフをかいてみましょう。
例題 $y=\dfrac{6}{x}$のグラフをかけ。
手順① 通る点の座標を10か所位求める
$y=\dfrac{6}{x}$の$x$に適当に数値をあてはめ、その時の$y$の値を求めます。
すると$x=1$のとき$y=6$なので$(1,6)$を通ります。
同様に$x=2$のとき$y=3$なので$(2,3)$を通り、
$x=3$のとき$y=2$ より $(3,2)$
$x=6$のとき$y=1$ より $(6,1)$をそれぞれ通ります。
これらの通る点を曲線になるように結べば完成、・・・ではありません。
ここで終わって正解なのは小学生まで。中学生は負の数を学びました。なので、$x$が負の値のときも考えていきます。
すると$x$と$y$には次のような表が完成します。
| $x$ | ・・・ | $-6$ | $-3$ | $-2$ | $-1$ | $0$ | $1$ | $2$ | $3$ | $6$ | ・・・ |
| $y$ | ・・・ | $-1$ | $-2$ | $-3$ | $-6$ | - | $6$ | $3$ | $2$ | $1$ | ・・・ |
手順② 求めた座標を曲線になるように結ぶ。比例定数が正の値なので、第一象限と第三象限にグラフをかく。

注意点
- グラフは絶対に軸に触れてはいけない
- 定規を使わないでかく
- グラフは丸みをもたせ、角を作らない
- グラフは無限に続くので、座標平面内では線を切らない
参考までに、$y=-\dfrac{6}{x}$のグラフもかいてみます。
$-$があるので比例定数は$-6$です。
よって第二象限と第四象限にグラフをかくので次のようになります。

