中学数学では、図形を使った証明問題の多くは三角形の合同を使います。
三角形の合同を使った証明問題は主に次のタイプのものがあります。
- 単純に2つの三角形の合同を証明するタイプ
- 三角形の合同を証明したうえで辺の長さや角の大きさが等しいことを説明するタイプ
- 三角形の合同を証明したうえで別の図形ができることを説明するタイプ
①よりも②、②よりも③と証明は長く複雑になりますが、どれも証明の基本にある考え方は同じです。
そのため、証明の書き方のコツをつかんでしまえば意外と簡単に証明できてしまいます。
このページでは、証明の仕方、書き方の流れを基本からじっくり解説します。
三角形の合同を使った証明の書き方
三角形の合同を使った証明問題の書き方には一定の流れがあります。
ひとまず証明の仕方の流れを簡単におさえておきましょう。

三角形の合同を使った証明問題の書き方の流れ
(1)合同を証明する三角形について記す
(2)三角形の合同条件を述べる
(3)だから合同だ、と結論づける
この3段階の流れで証明を進めます。
「(2)三角形の合同条件を述べる」ために(1)と(2)の間であ~だ、こ~だと理屈を並べるわけです。この、あ~だ、こ~だと理屈を並べる所が証明問題を難しく感じさせてしまうのです。
それでは早速、超基本例題を使って証明の流れをつかんでいきましょう。
超基本例題
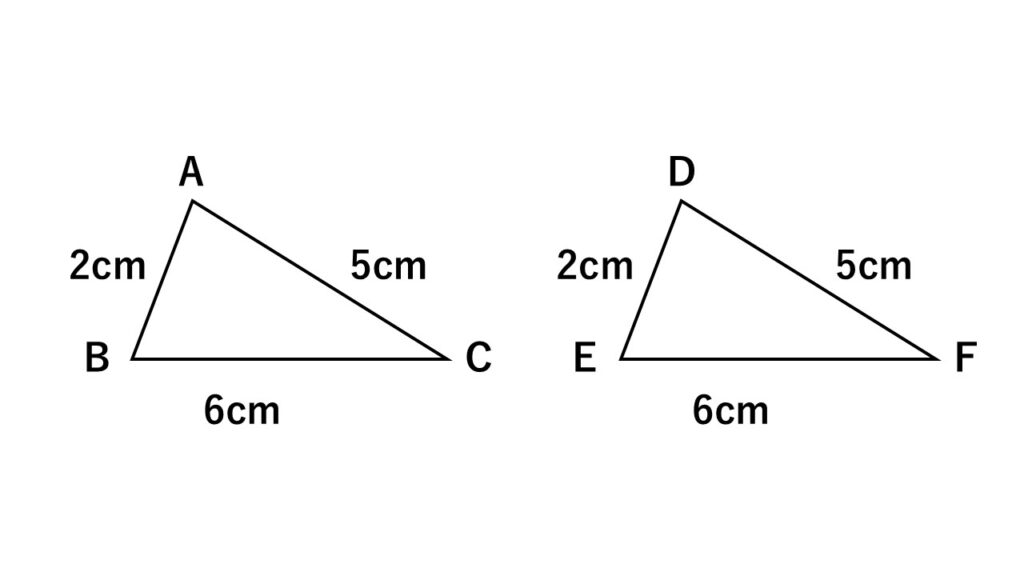
図のような2つの三角形$△ABC$と$△DEF$がある。
この2つの三角形が合同であることを証明せよ。
証明
$△ABC$と$△DEF$において
図より対応する辺なので
$\begin{align}AB&=DE&①\\
BC&=EF&②\\
CA&=FD&③\end{align}$
①②③より3組の辺がそれぞれ等しいので
$△ABC≡△DEF$ である
証明終わり
上記POINTで紹介した証明問題の書き方の流れに沿っていることを確認してください。
実際にはここまで単純な証明問題は出題されません。ただここでは証明のコツをつかんでもらうために、あえて単純な問題を例題にしました。
それでは証明の書き方について、以下じっくり解説していきます。
証明
←証明を始める時に必ず一言加える。
$△ABC$と$△DEF$において
←流れ(1) これから合同を証明する三角形について記号△を使って表す。
アルファベットは対応する順に並べるのが原則。
図より対応する辺なので
$\begin{align}AB&=DE&①\\
BC&=EF&②\\
CA&=FD&③\end{align}$
←合同条件を述べるための準備。
問題に与えられた条件をそのまま書くので、
「図より」と一言。「仮定より」と書いても間違いではない。
「対応する辺なので」と加えるとより丁寧な証明になる。もっとも図から明らかなので書く必要はないが。
「3組の辺がそれぞれ等しい」が言えそうなので、対応する辺が等しいことを示す。
証明が長くなるときは、①②③と番号をつけておくと少し楽に進められる。
①②③より3組の辺がそれぞれ等しいので
←流れ(2)合同条件を述べる。
$△ABC≡△DEF$ である
←流れ(3) この一言が抜けると証明の意味がない。
証明終わり
←この一言も忘れずに
この例題と証明をそのまま暗記して、証明の書き方の流れを覚えてしまいましょう。
証明するときは
「どうしてそのようなことが言えるのか」の理由を1つ1つ丁寧に表現していく必要があります。
そのため合同条件をいう前に、
$\begin{align}AB&=DE&①\\
BC&=EF&②\\
CA&=FD&③\end{align}$
と説明するわけです。さらに、
いきなり
$\begin{align}AB&=DE&①\\
BC&=EF&②\\
CA&=FD&③\end{align}$
を書くのではなく、「仮定より」とか「図より対応する辺なので」と理由を加えるようにします。
ところで例題解説の中で「仮定」や「結論」といった言葉が出てきました。
証明する際によく使う言葉なので簡単にまとめておきます。
仮定と結論 定義と定理
仮定と結論
「$p$ならば$q$である(になる)」という形で書かれたときの、$p$の部分を仮定、$q$の部分を結論
といいます。
「三角形の合同条件をいえる(仮定)ならば2つの三角形は合同(結論)である」
といった具合ですね。
他にも、
$1+1$ならば$2$である
も立派な仮定と結論です。
この仮定と結論。何も数学の世界だけのお話ではなく、日常にも普通にあります。
朝のじゃんけんの時に起きたならば寝坊である
寝坊したならば食パンをくわえながら走って通学することになる
赤信号ならば止まれである
8時35分を過ぎるならば遅刻である
グランド10周走らされているならば遅刻した証拠である
例を挙げるときりがないですが、「○○ならば□□である」の形になっていることをおさえてください。
定義と定理
定義・・・人間が勝手に決めた約束事、ルールのこと。
定理・・・ざっくりいうと性質のこと。もう少し詳しくいうと、既にその性質の正しさが証明されている変えようのない事実のこと。
例えば二等辺三角形の定義といったら、
「三角形はいろんな形のものがあるけど、2つの辺の長さが等しい三角形のことを二等辺三角形ということにしましょう」ということになります。
他にも例えば、平行の定義といったら
「同一の平面上にあってどこまで延長しても交わらない2本以上の直線のことを平行ということにしましょう」となります。
定義。勝手に決めた約束事なので、変えようと思えばいくらでも変えられます。
そのため、今は「2つの辺の長さが等しい三角形のことを二等辺三角形」としていますが、もしかしたら将来「2つの辺の長さが等しい三角形」が別の名称に変わってしまうこともあるわけです。
もしかしたら将来、平行という言葉は別の表現に変わるかもしれません。
逆に言えば、今の時点で特に約束事が決まっていないことがあれば、新たに定義として世の中に広めることだってできるわけです。世間が認めれば、ですが・・・。
一方の定理ですが、こちらは性質のことなので変えようがありません。
さらにその性質の正しさを証明されていることが前提なので、定理は定理として受け入れざるを得ないということです。
例えば「二等辺三角形の底角は等しい」というのがありますが、これは定理です。
二等辺三角形の性質として、その正しさが証明されています。
他にも定理はたくさんあります。このサイトでも都度定理を紹介していきます。
三角形の合同を証明したうえで長さが等しいことを示す
再び三角形の合同の証明に戻ります。
今度は教科書や問題集などによく掲載されている代表的な証明問題を使って、証明の仕方を確認していきます。
証明問題の書き方の流れをふまえていることを確認してください。
基本例題
線分$AB$と$CD$の交点を$E$とする。
$EA=EB、ED=EC$であるとき、
$AD=BC$となることを証明せよ。

この例題も先の超基本例題と同様、例題と証明をそのまま覚えてしまってください。
といっても証明の書き方に慣れるために、少し自力で考えてみましょう。
考え方
$AD$と$BC$が同じ長さであることを示す。そのためにどうすれば良いか?ということです。
図と問題の条件に与えられていること(仮定)をもとに証明を進めます。
当然定規を使って長さを測るのはNG。
ここで思い浮かべてほしいのが、
「対応する辺は長さが等しい」ということ。
三角形の合同を証明したうえで対応する辺の長さに言及すれば、結果として長さが等しいでしょ、となるわけです。
ということで証明に入ります。
証明
$△AED$と$△BEC$において
←流れ(1)
対応する順にアルファベットを書いていることにも注目。
仮定より
$\begin{align}EA&=EB&①\\
ED&=EC&②\end{align}$
←問題の条件をそのまま述べているため仮定になる。①②と番号をつけておくと後でラク。
対頂角は等しいので
$∠AED=∠BEC$ ③
←問題には書かれていない隠れた条件。
そのため仮定ではない。
①②③より
2組の辺とその間の角がそれぞれ等しいので
←流れ(2)
$△AED≡△BEC$
←流れ(3)
ここで終わってはダメ。
したがって
合同な図形の対応する辺の長さは等しいから
$AD=BC$となる
証明終わり
←$AD=BC$となる理由を必ず述べる。
この一文が抜けてしまうとテストでは大きな減点になるので要注意。
この基本例題は単に合同を証明して終わりではなく、合同を証明した上で対応する辺の長さが等しいことを示しました。
このように、合同を証明したうえで長さや角の大きさが等しいことを示す問題、あるいは別の図形ができることを示す問題が、定期テストや入試では一般的に出題されます。
証明に慣れないうちは長く感じたり、そもそも何をやっていたのかを忘れてしまったりすることもあるでしょう。
ただ1つ1つ頭の中を整理して考えていけば、決して難しいことでもないと理解できると思います。
