円周角の定理の逆とはものすごくざっくり言ってしまえば、
2つの角の大きさが等しければ4点A,B,C,Dは同一円周上にある
というものです。
ただこの書き方は、円周角の定理の逆をざっくり示しているため全く説明になってないのも確かです。
ということで図を見ながら円周角の定理の逆を詳しく見ていきましょう。
円周角の定理の逆を図で理解する
円周角の定理の逆を正確に書くと次のようになります。
円周角の定理の逆
4点$A,B,C,D$があり、線分$AB$を考える。
このとき$C,D$が線分$AB$に対し同じ側にあり、
$\angle ACB=\angle ADB\:$ならば
4点$A,B,C,D$は同一円周上にある。
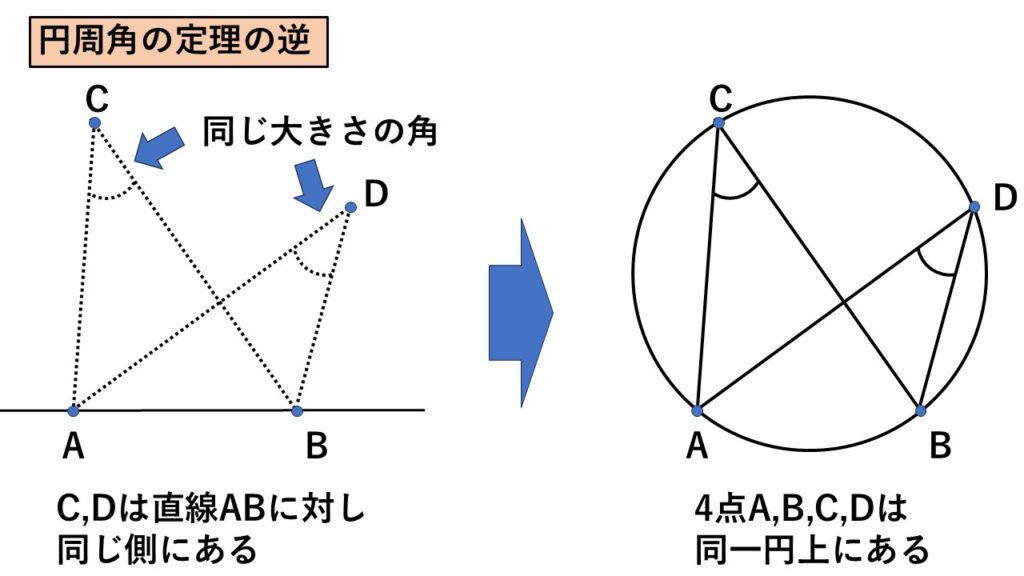
「$C,D$が線分$AB$に対し同じ側にあり」というところが重要!!
円周角の定理は「同じ孤に対する円周角はどれも等しくなる」というものでした。
一方、円周角の定理の逆はまさにその逆、
冒頭にも書いた通り2つの角が等しければ4点は同一円周上にある
ということになります。
（言葉で正確に表すのは意外と難しいし、正確に表したものを読むのもハードルが高い。）
とりあえず円周角の定理の逆に慣れるまでは「2つの角が等しければ4点は同一円周上にある」と覚えましょう。
そして慣れてきたらPOINTに書いたように正確に覚えるようにすると良いでしょう。
では円周角の定理の逆を使った基本的な問題を解いて理解していきます。
基本例題1
次の$(1)$～$(3)$の図で、4点が同一円周上にあるものを選べ。
考え方
与えられた4点が同一円周上にあるのかどうかを調べるには、円周角の定理の逆を使います。
$(1)\:$線分$AB$を考え、これに対し同じ側にある点$C,D$について注目します。
$(2)\:(1)$と同様、線分$AB$を考えた方が良さそうです。
$(3)\:$円周角の定理の逆を使うためにはどこの角に着目すれば良いかを考えましょう。
解答
$(1)$と$(3)$
解説
$(1)\:$POINTの図そのままの問題です。これは瞬間的に解答できてほしい問題です。
考え方では「線分$AB$を考える」と書きましたが、 これは言い換えると「ひとまず弧$AB$を考えている」ということでもあります。
弧$AB$に対する円周角$\angle ACB$と$\angle ADB$の角度を考えています。
$(2)\:$弧$AB$を考えその円周角の大きさ、$\angle ACB$と$\angle ADB$を調べます。
平行線と錯角の関係から
$\quad\angle ADB=25°$より
$\quad\angle ACB$と大きさが異なるため同一円周上ではないといえます。
$(3)\:(2)$と同様弧$AB$を考えその円周角の大きさ、$\angle ACB$と$\angle ADB$を調べます。
図から直角二等辺三角形が2つあるとわかります。
$\quad\angle ADB=\angle ACB=45°$より
同一円周上にあることがわかります。
$(1)$のように2つの三角形がつながった状態で出題される円周角の定理の逆を使った問題は、最も基本的なものといえます。
そして三角形がつながっている形だからこそ、円周角の定理の逆を使うものだと判断しやすいともいえます。
最も基本的で円周角の定理の逆を使えば良いと判断しやすい問題。
そう、つまり$(1)$のような問題は簡単すぎて高校入試では出題されません。
高校入試ではひとひねり加えた形で出題されます。そのひねりが$(3)$のように四角形として出題されるもの。
ただ四角形で出題されたとしても、$(1)$のような三角形を見つけて考えればたいていの問題は解答できます。
なぜ円周角の定理の逆が成り立つのか
次になぜ円周角の定理の逆が成り立つのかを考えます。
円周角の定理の逆、つまり
4点$A,B,C,D$があり、$C,D$が線分$AB$に対し同じ側にあるとき
$\angle ACB=\angle ADB\:$ならば
4点$A,B,C,D$は同一円周上にある
ことがなぜ成り立つのか。
ここでいきなり理由の説明に入る前に、ちょっと頭の中を整理しておきましょう。
角度が異なることに着目する
円周角の定理の逆が成り立つことを示すには
円周角の定理が正しいことが分かっている
ということが前提になります。
そのうえで、
「同一円周上にある点がつくる角（図では$C,D$のこと）はどれも同じ大きさになる」から、
同一円周上にない点がつくる角は図の$\angle c$や$\angle d$と異なる大きさになる
ことを示します。
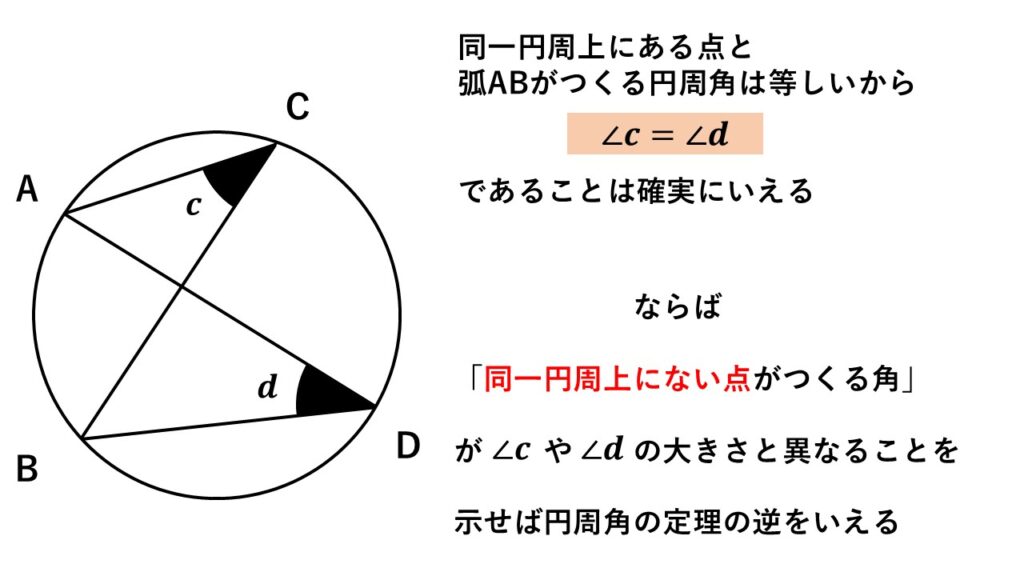
同一円周上にない点。
つまり円の外側や内側にある点と円周上の点（弧$AB$をつくる点のこと）とでつくる三角形に注目します。
そしてその円の外部の点や内部の点がつくる角が、弧$AB$に対する円周角$\angle c$や$\angle d$と大きさが異なることを示します。
要するに
円の外側に点があると角の大きさが違うじゃん
↓
円の内側に点があっても角の大きさが違うじゃん
↓
ってことは円周上にある点じゃないと同じ角の大きさにならないじゃん
↓
だから2つの角の大きさが等しければ4点は同一円周上にあるんだ
といった論調で説明していきます。
円周角の定理の逆が成り立つ理由
①円の外部に点があるとき
円の外側に点$P$を取り、$\triangle ADP$を考える。
ここで$\angle d$は三角形の外角になるので、
$\angle a+\angle p=\angle d$
これより
$\angle a+\angle p-\angle a=\angle d-\angle a$
となるから
$\angle p<\angle d$
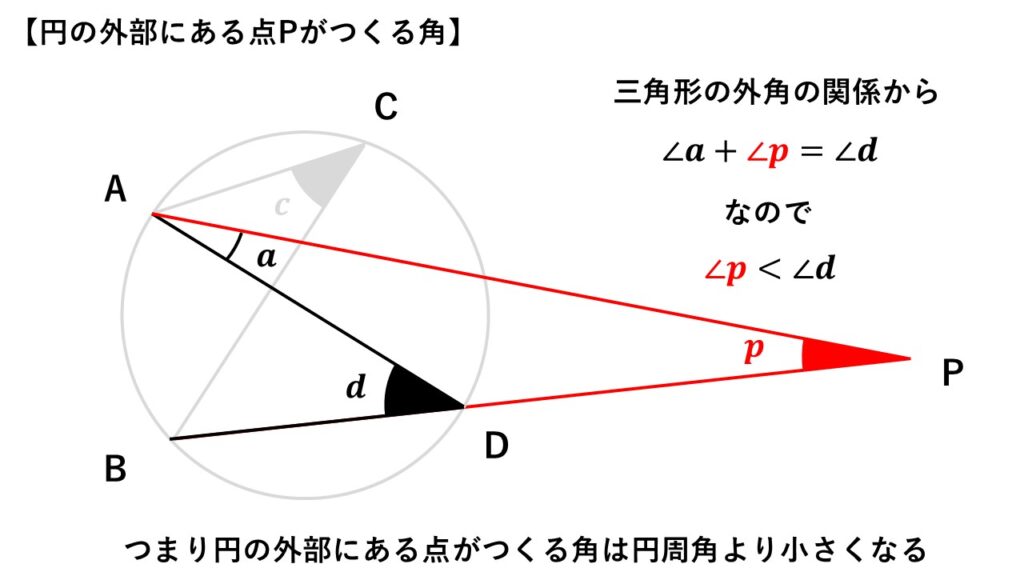
点$C$と点$D$は同一円周上の点なので円周角の定理から
$\angle c=\angle d$
よって$\:\angle p<\angle c$
したがって円の外部にある点がつくる角は円周角よりも小さくなる。
②円の内部に点があるとき
円の内側に点$Q$を取り、$\triangle QBD$を考える。
ここで$\angle q$は三角形の外角になるので、
$\angle b+\angle d=\angle q$
これより
$\angle b+\angle d-\angle b=\angle q-\angle b$
となるから
$\angle d<\angle q$
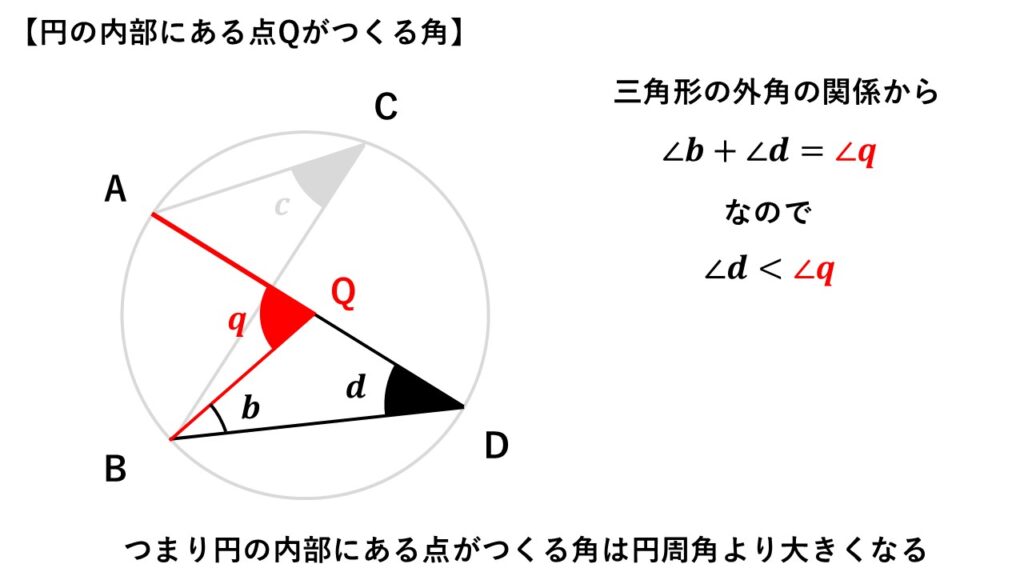
点$C$と点$D$は同一円周上の点なので円周角の定理から
$\angle c=\angle d$
よって$\:\angle c<\angle q$
したがって円の内部にある点がつくる角は円周角よりも大きくなる。
これらのことから
4点が同一円周上にあるときに限り、弧$AB$に対する円周角の大きさが等しくなる。
よって
4点$A,B,C,D$があり、$C,D$が線分$AB$に対し同じ側にあるとき
$\angle ACB=\angle ADB\:$ならば
4点$A,B,C,D$は同一円周上にある
といえる
円周角の定理の逆の証明は理屈自体は簡単です。
ただその証明を考えるには円の外と内に目を向けるということで、ちょっとした視点の切りかえが必要です。
そしてそこが証明を難しく思わせてしまうところでもあります。
もっとも円周角の定理の逆は、その性質を使って角度を求めたり、他の図形と関連させて考える問題のほうが入試等々での出題頻度が高いようです。
円周角の定理の逆の証明は理屈を簡単に押さえておいて、基本例題1のような問題に慣れてきてから証明をできるようにしましょう。