円周角の定理とその証明

円周角の定理。覚える内容ははっきりいって簡単。
テストで出題されたら正答必須。
だからこそ初歩的な練習問題を何度も繰り返し練習して、円周角と中心角の問題は必ず解けるようにしておきましょう。

円周角とは

円周上に2点$A,B$を取り、さらにもう1点$C$を取り、弧$AB$の両端からそれぞれ点$C$を結びます。
そのときできる

$\angle ACB$を円周角

といいます。

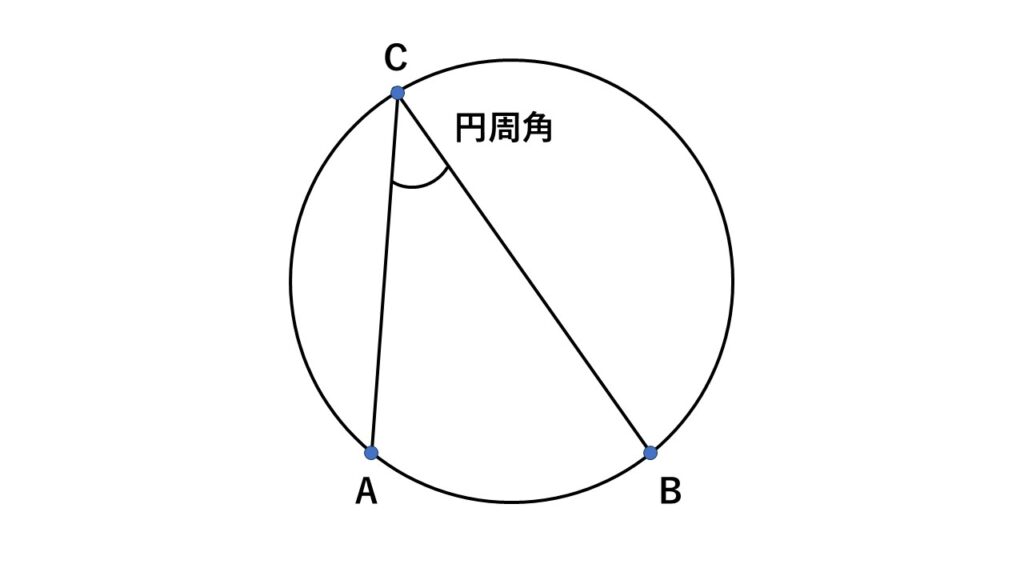
特に、どの弧についての円周角なのかをはっきりさせる場合は、
「弧$AB$に対する円周角」
という言い方をします。

円周角の性質

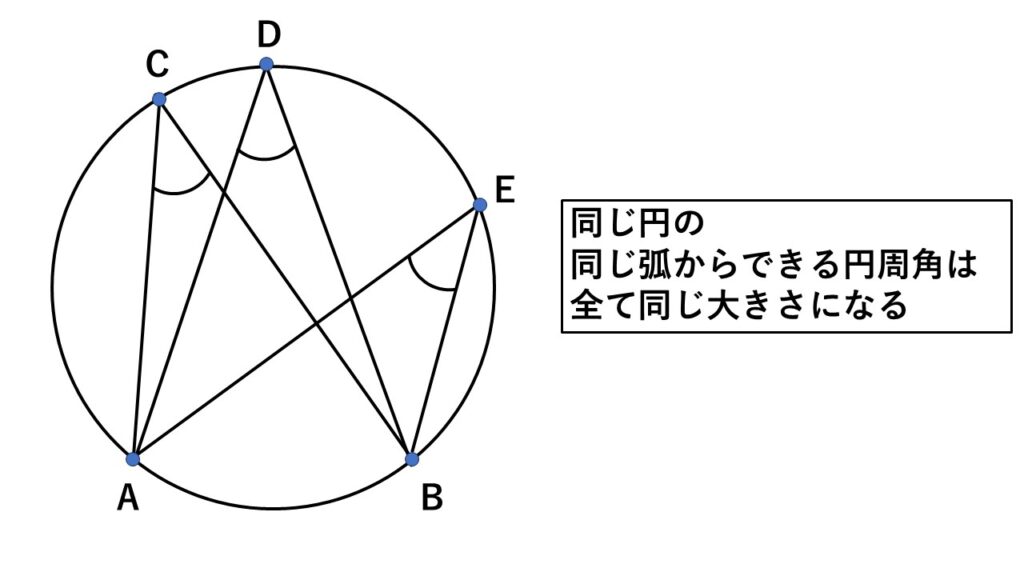
1つの弧に対する円周角はどれも同じ大きさになる

図の場合、弧$AB$に対する円周角は
$\angle ACB,\angle ADB,\angle AEB$
と3つありますが、どれも同じ大きさです。

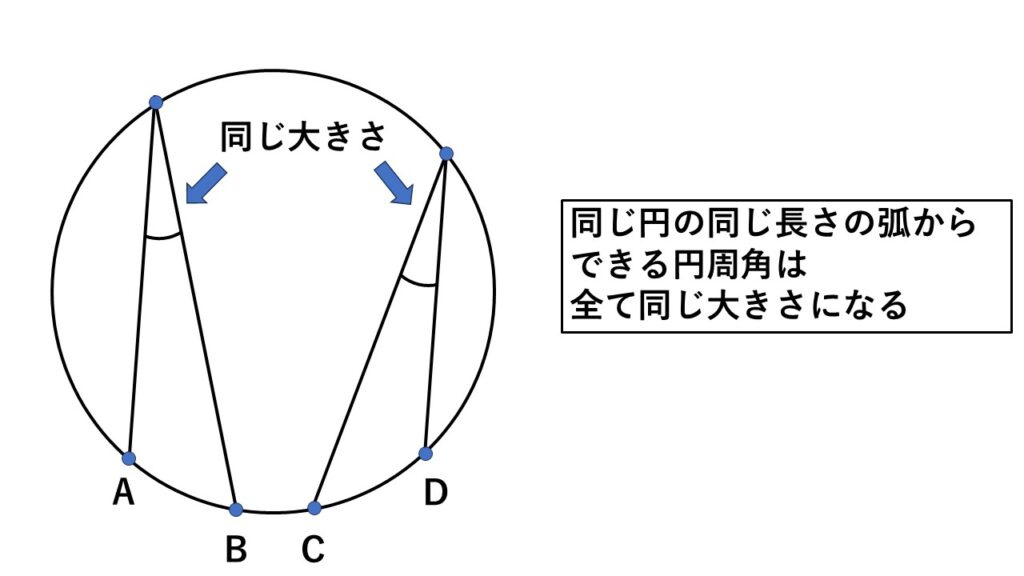
同じ円の同じ長さの弧からできる円周角は同じ大きさになる

図の場合、弧$AB$と弧$CD$が同じ長さなら円周角は同じ大きさです。
逆に、同じ円において円周角が同じ大きさなら、それに対する弧の長さも同じになります。

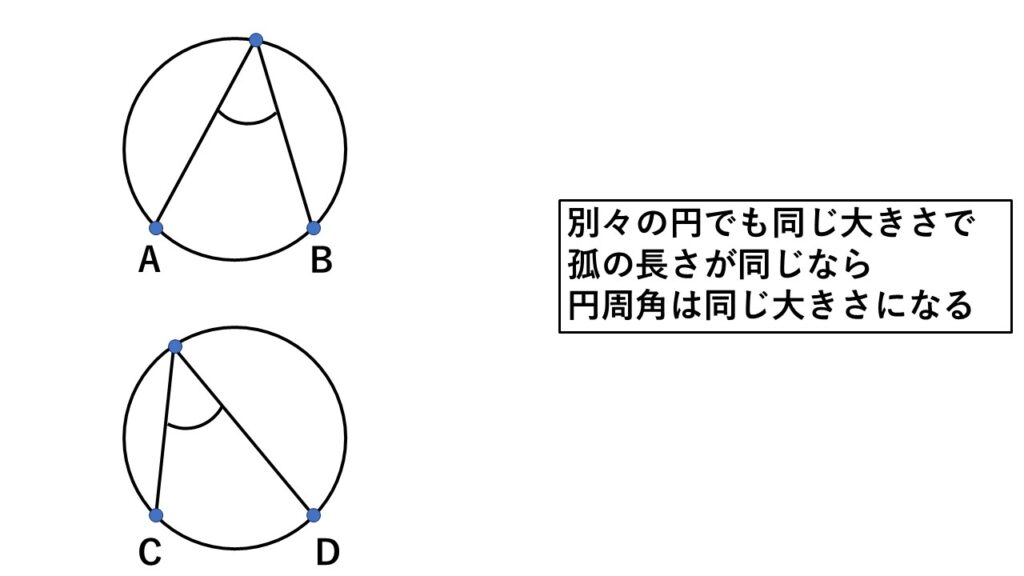
異なる円でも大きさが同じで弧の長さも同じなら、それらの弧に対する円周角は同じ大きさになる

上記2番目の性質からこのこともいえます。
逆に、異なる円でも大きさが同じで円周角も同じ大きさなら、その弧の長さも同じ長さになります。

注意!!
1つの円において弧$AB$といった場合、弧は2種類考えられます。
図では$A$から$C$を通って$B$に行く弧と、$A$から$D$を通って$B$に行く弧の2つがあります。

単純に弧$AB$といった場合、どちらの弧を表すか判断がつかないので、誤解が生じないように表す必要があります。

中心角とは

円周上に2点$A,B$を取り、その2点から円の半径を引くときにできる半径と半径に挟まれた

$\angle AOB$を中心角

といいます。

弧$AB$に対する円周角の大きさは弧$AB$に対する中心角の$\dfrac{1}{2}$になります。

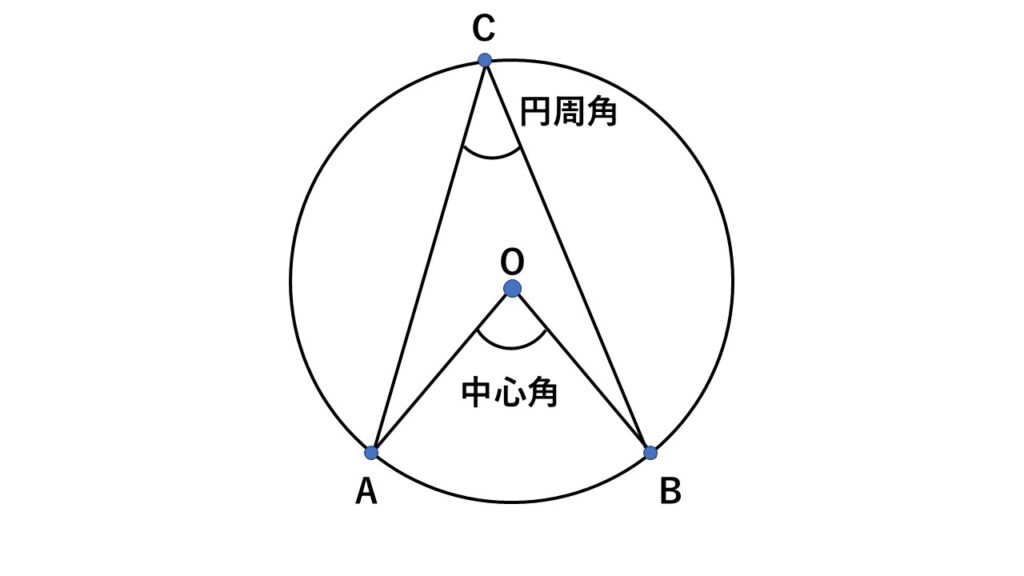
例えばPOINTの図で、中心角が$80°$の場合、円周角は$40°$となります。

この円周角と中心角の分野に関して、覚えるべき事柄は以上です。
簡単ですよね？　量も少ないし。

で、こう書くと勘が鋭い人は薄々気づいてると思います。
そう、円周角や中心角の問題はそれ単体で出題したら、それなりに勉強した人ならみんな正解できます。
なので特に高校入試では、今まで学習した図形との融合問題として出題されることがほとんどです。

だからこそ「円周角や中心角は簡単だ!!」で終わらせるのではなく、今まで学習した図形の知識も併せて確認することが重要になってきます。

ということで基本例題を通して円周角や中心角だけでなく、その他の図形の知識も併せて練習していきましょう。

基本例題1
図の$(1)$～$(6)$の$x$の角度をそれぞれ求めよ。

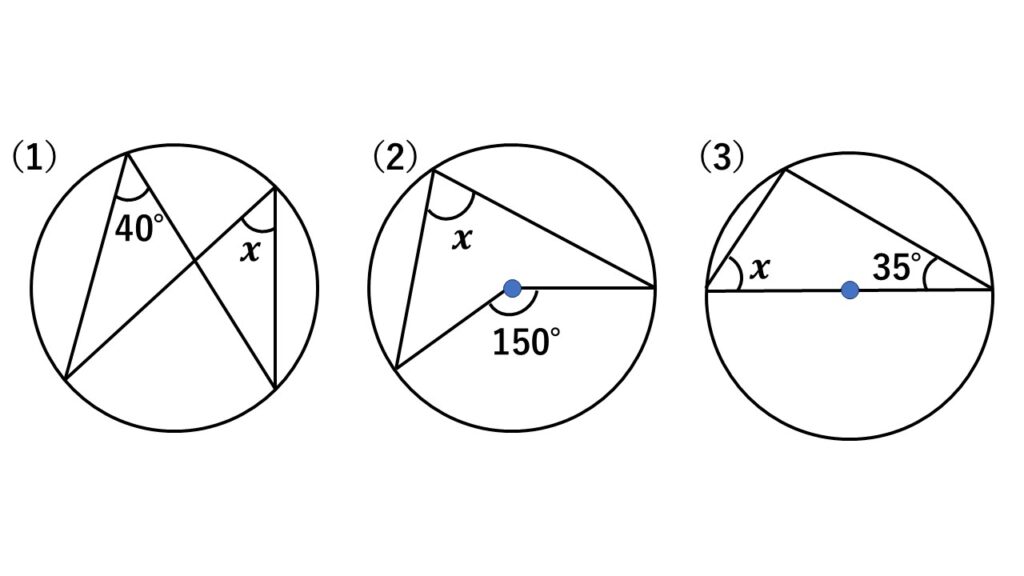
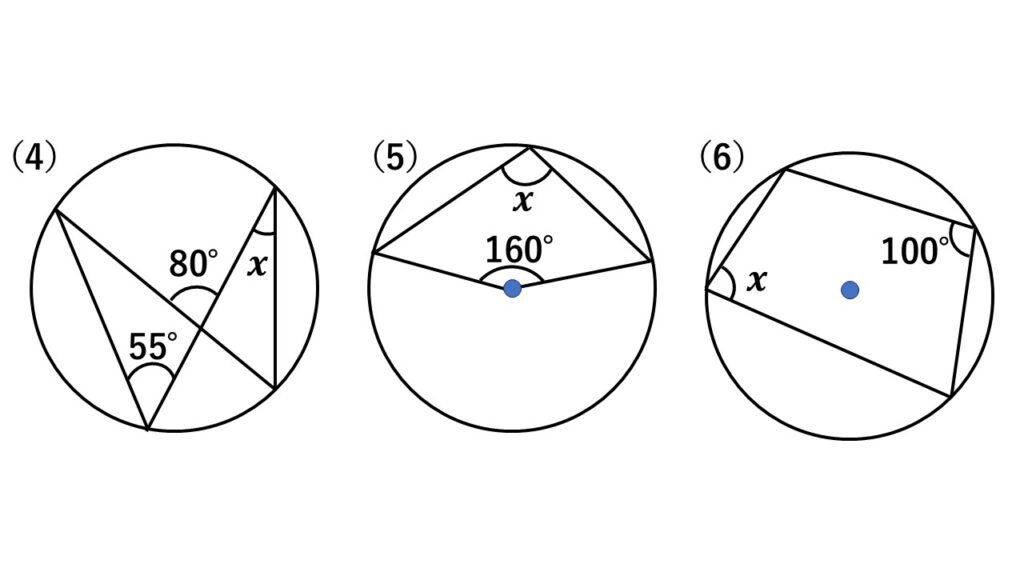
考え方
考え方を書くとそれが即解答になってしまうので、ここはじっくり考えてください。

解答
$(1)\:40°\quad(2)\:75°\quad(3)\:55°$
$(4)\:25°\quad(5)\:100°\quad(6)\:80°$

解説
$(1),(2)$はノーヒントで必ず正答できなければいけません。

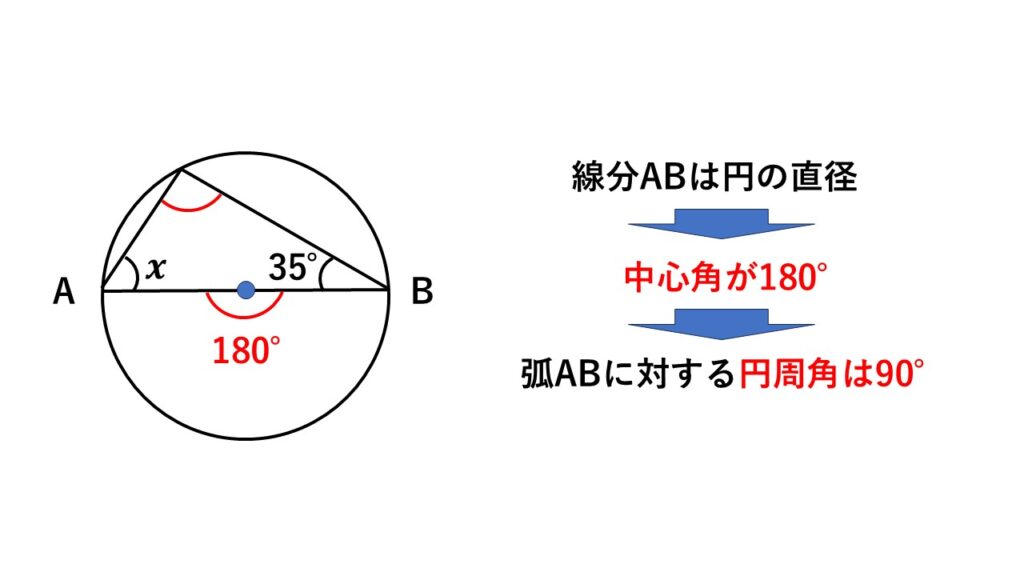
$(3)\:$線分$AB$が円の直径であることに気づけることがポイント。
このとき弧$AB$に対する中心角は$180°$です。
すると円周角を求められ、$x$の値も求まります。

円の直径に対する円周角は$90°$

この関係はよく使うのでこのまま覚えておきましょう。

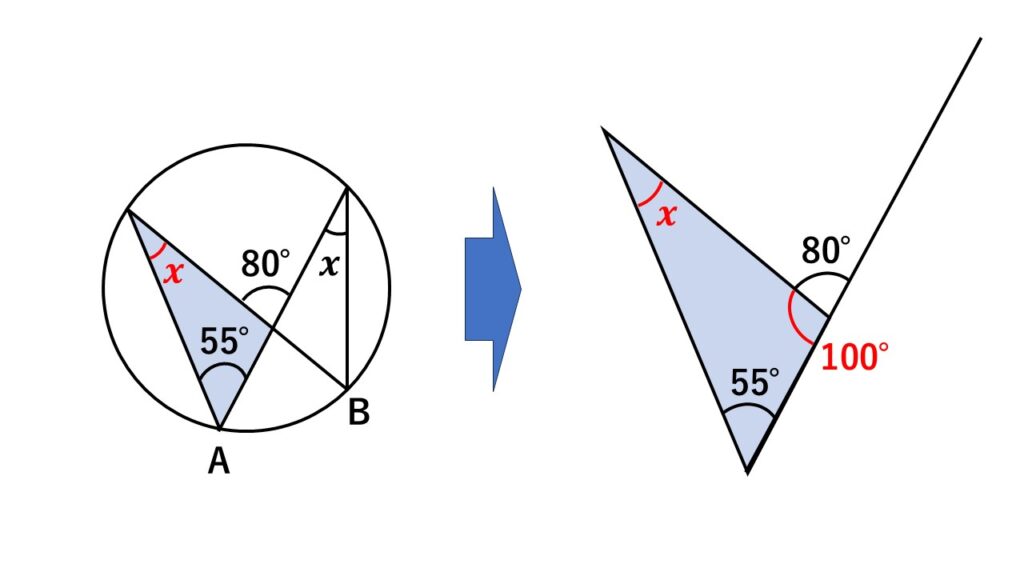
$(4)\:$左の三角形に注目すると、弧$AB$の円周角として$x$を表せます。
また$80°$を手がかりに、1つの内角が$100°$であることもわかります。
これで$x$を求められます。

なお、三角形の1つの外角はそれと隣り合わない2つの内角の和に等しいことを使えば、
$80=x+55$より$25°$が求まります。

$(5)\:$間違えやすい問題の1つです。
上記の注意!!で書きましたが、単に弧$AB$とした場合、2種類が考えられます。
そこを突いたのがこの問題。
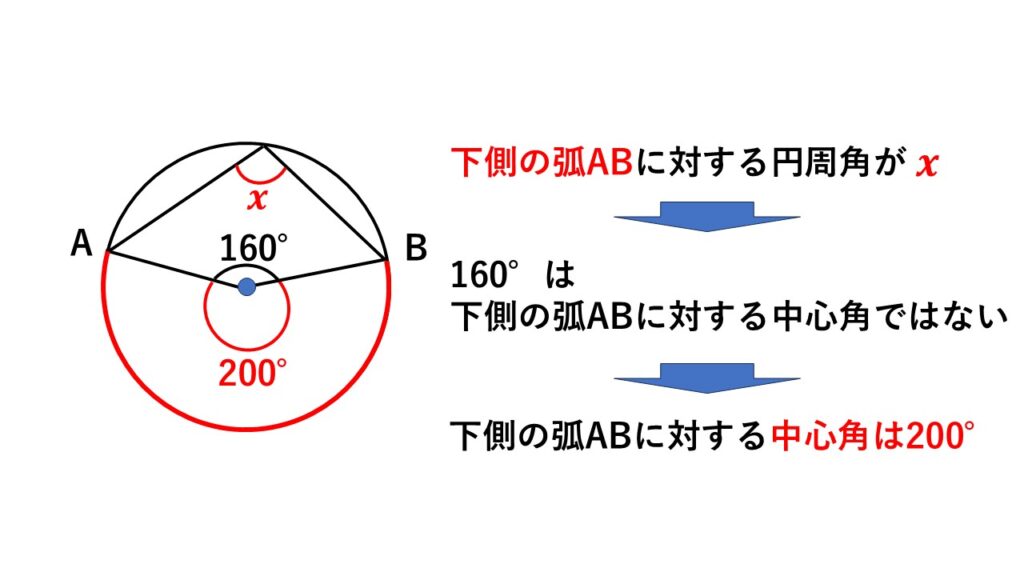
この問題の場合、弧$AB$は上側のものと下側（赤で色付けした部分）のものとに分かれます。
求める$x$は下側の弧$AB$に対する円周角。よって$160°$は下側の弧の中心角ではありません。
$160°$は上側の弧$AB$に対する中心角です。

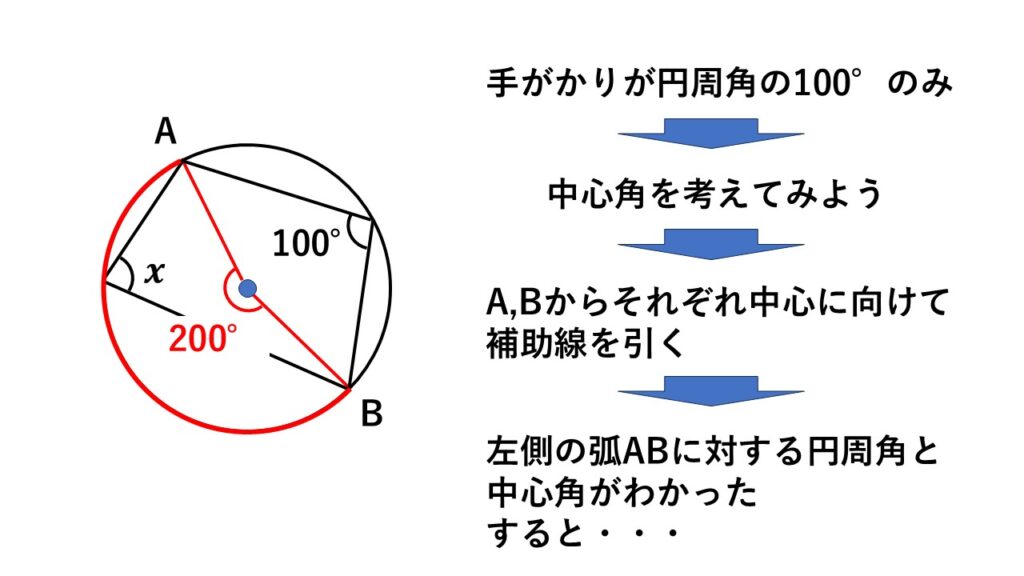
$(6)\:$手がかりが円周角の$100°$しかないので、中心角を求めます。そこで必要なのが円の中心と四角形の頂点を結ぶ補助線。
これより左側の弧$AB$に対する円周角と中心角がわかります。
すると中心角の残りの大きさがわかり、$x$も求まります。
実は$(5)$は$(6)$のヒントでした。

ところで$(6)\:$の図。
このように四角形の4つの頂点全てが円周上にあるときには、とある性質が見えてきます。
基本例題1の$(6)$の図をもう少し深堀します。

円に内接する四角形について

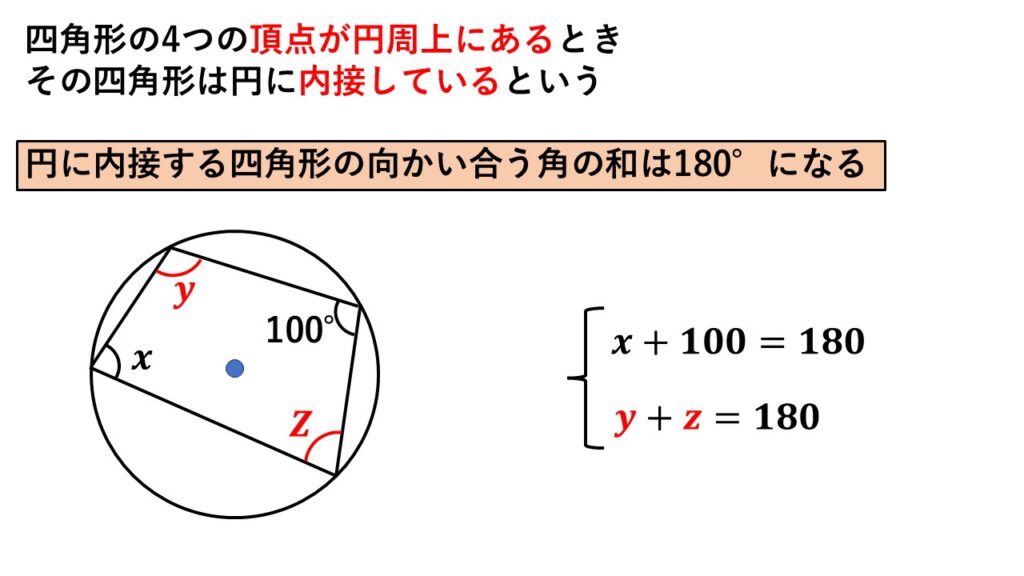
円の内側に四角形があり、なおかつその4つの頂点が円周上にあるときその四角形は

円に内接している

といいます。また、

円に内接する四角形の向かい合う角を足すと、その結果は$180°$になります。

このことを知っていると、基本例題1$(6)\:$は瞬時に$x=80$と求まります。

どうしてそのようなことがいえるのかは、基本例題1$(6)\:$の解答でほぼほぼ説明できています。
今後円に内接する四角形の角度の問題が出たら、数値だけを答えればよい場合は上記の性質を使ってサクッと答えてしまいましょう。

ここまでのまとめ

ここでいったん円周角の定理についてまとめておきます。

円周角の定理

• 1つの弧に対する円周角はどれも同じ大きさになる
• 1つの孤に対する円周角は中心角の$\dfrac{1}{2}$となる

そして円周角の定理がいえることによって

• 同じ円の同じ長さの弧からできる円周角は同じ大きさになる
• 逆に、同じ円で円周角が同じ大きさならば弧の長さも同じになる

ということがいえます。

これらのことと今まで学習してきた図形の知識を合わせると、
基本例題1$(3)$の円の直径に対する円周角は$90°$や、
$(6)$の円に内接する四角形の向い合う角の和は$180°$
がわかってきます。

ここまで決して難しいことをやっているわけではないので、しっかり覚えておきましょう。

次に一歩踏み込んで、円周角の定理が成り立つ理由についてみていきます。
こちらも覚えておくべき内容ですが、上記までの内容を理解するのが最優先です。
円周角や中心角の問題を解けるようにしてから読み進めてください。

なぜ円周角の定理が成り立つのか

円周角の定理が成り立つ理由は、

中心角が円周角の2倍になることを示せば証明したことになります。

そのためには3つの視点から考える必要があります。

その3つの視点とは「円周角と円の中心の位置関係」について。
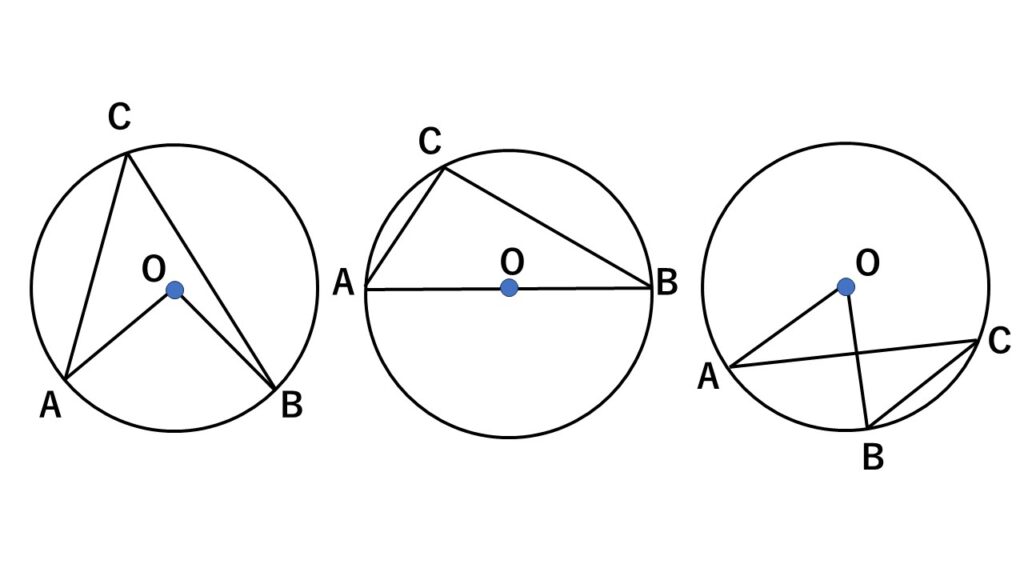
図のように

• 円の中心が円周角の内側にある
• 円の中心が$\triangle ABC$上にある
• 円の中心が円周角の外側にある

の3パターンについてそれぞれ、中心角が円周角の2倍になることを証明していきます。

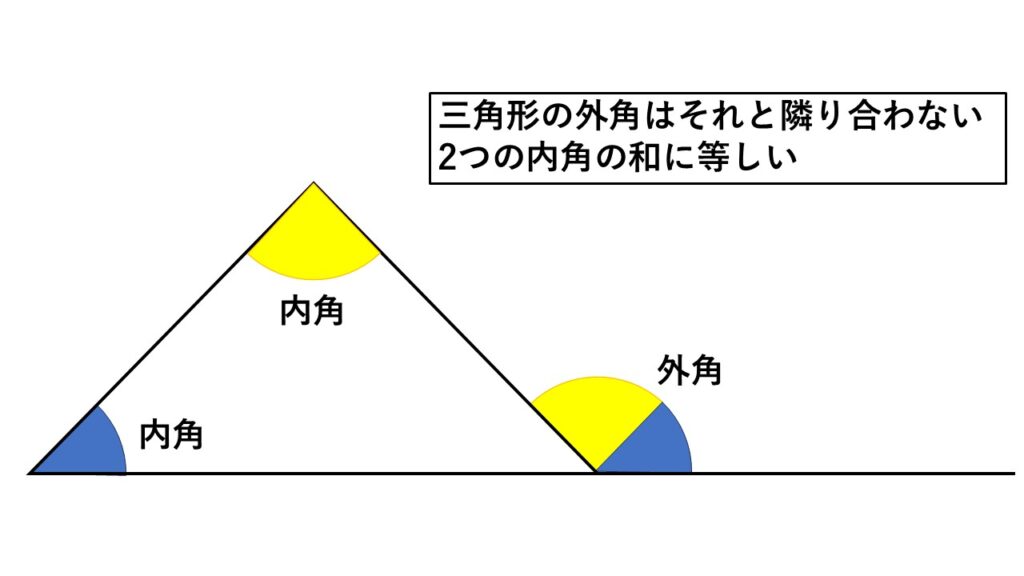
なお円周角が成り立つことを証明する際は、
二等辺三角形の底角は等しいこと、
三角形の外角はそれと隣り合わない2つの内角の和に等しいことをフル活用します。

忘れていた人は合わせて確認しておきましょう。

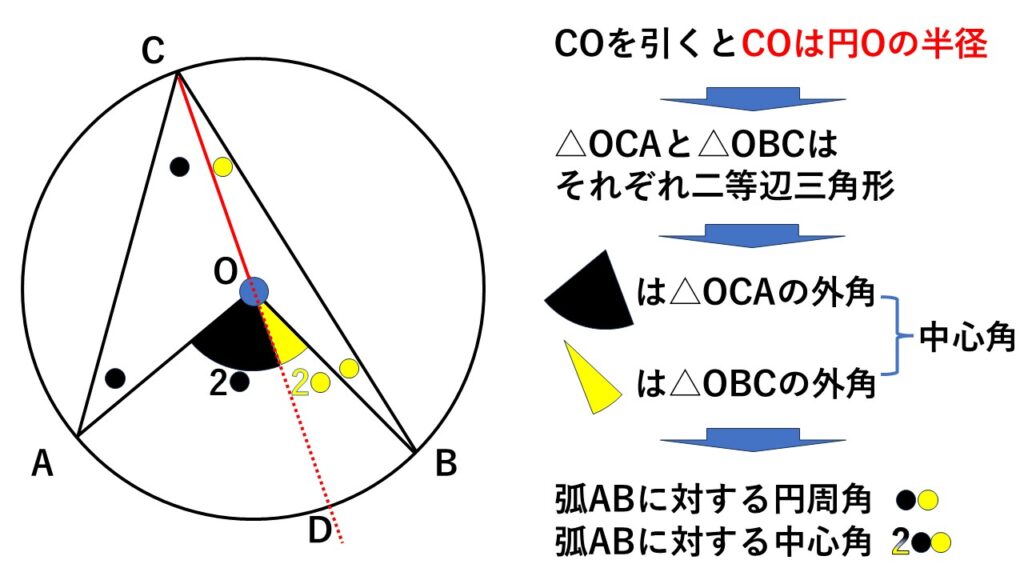
円の中心が円周角の内側にあるとき

点$C$から円の中心$O$に向かってまっすぐな線を引き円周との交点を$D$とする
すると$\triangle OCA$と$\triangle OBC$の2つの二等辺三角形ができる
三角形の外角の性質を使うと
$\begin{align}\angle AOD&=\angle OAC+\angle ACO\\&=2\angle ACD\quad①\end{align}$

$\begin{align}\angle BOD&=\angle OBC+\angle BCO\\&=2\angle BCD\quad②\end{align}$

ここで弧$AB$に対する円周角は
$\angle ACB=\angle ACD+\angle BCD\quad③$
また①②より弧$AB$に対する中心角は
$\begin{align}\angle AOB&=\angle AOD+\angle BOD\\&=2\angle ACD+2\angle BCD\\&=2(\angle ACD+\angle BCD)\\&=2\angle ACB\end{align}$

したがって中心角は円周角の2倍とわかる

円の中心が$\triangle ABC$上にあるとき

点$C$から円の中心$O$に向かって円の半径を引く
このときできる$\triangle OCA$と$\triangle OBC$は二等辺三角形になる
ここで三角形の外角の性質を使うと
$\begin{align}\angle COB&=\angle OAC+\angle OCA\\&=2\angle OCA\quad①\end{align}$

$\begin{align}\angle COA&=\angle OBC+\angle OCB\\&=2\angle OCB\quad②\end{align}$

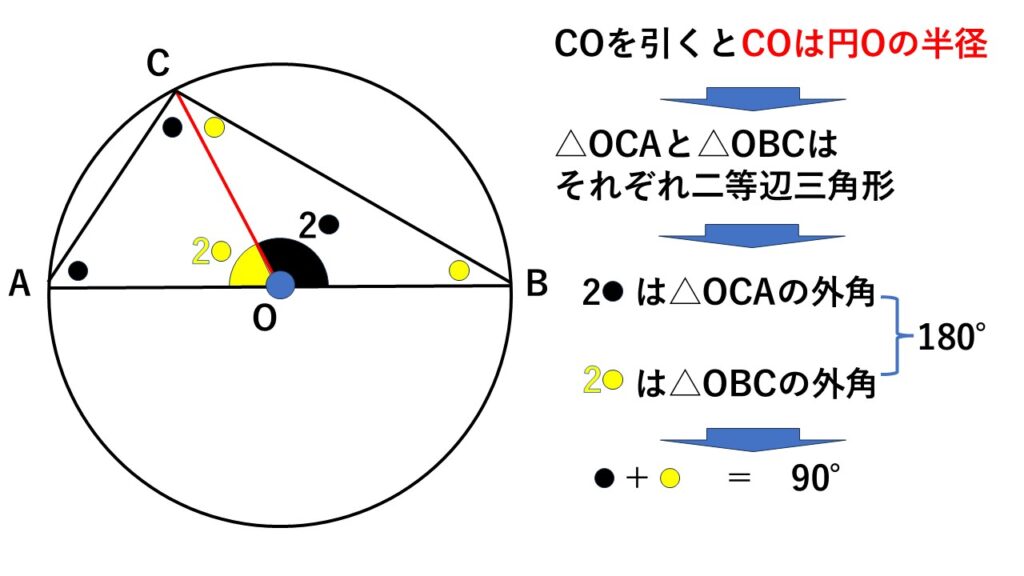
また直線は$180°$より①②から
$\begin{align}\angle AOB&=\angle COB+\angle COA\\&=2\angle OCA+2\angle OCB\\&=2(\angle OCA+\angle OCB)\\&=2\angle ACB=180°\end{align}$

したがって中心角は円周角の2倍とわかり、円の直径に対する円周角は$90°$ともわかる

円の中心が円周角の外側にあるとき

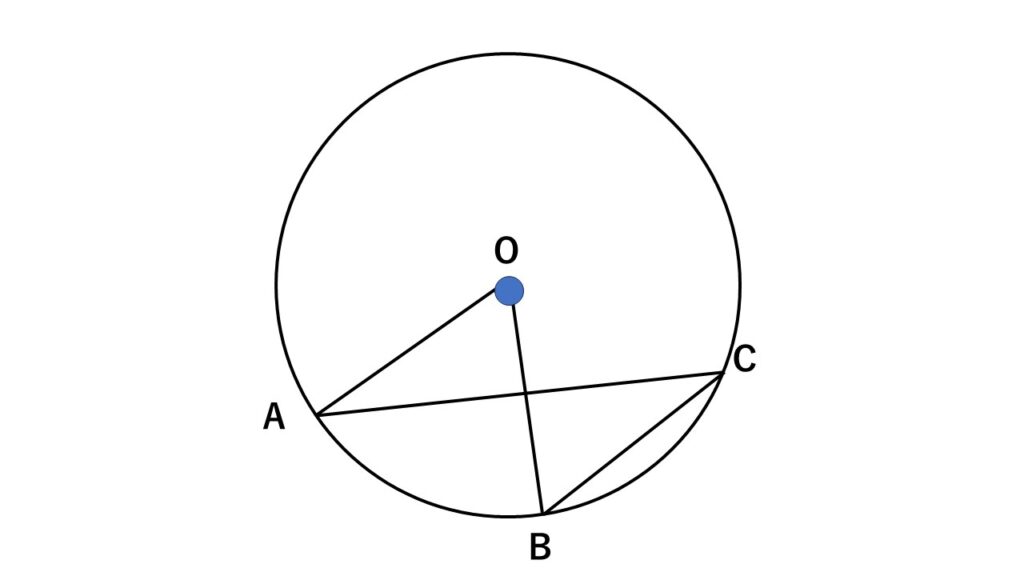
点$C$から円の中心に向けてまっすぐな線を引き、円周との交点を$D$とする

この際できる$\triangle OCA$と$\triangle OBC$はそれぞれ二等辺三角形となる

まず$\triangle OCA$に注目する

三角形の外角の性質を使うと
$\begin{align}\angle DOA&=\angle DCA+\angle OAC\\&=2\angle DCA\quad①\end{align}$

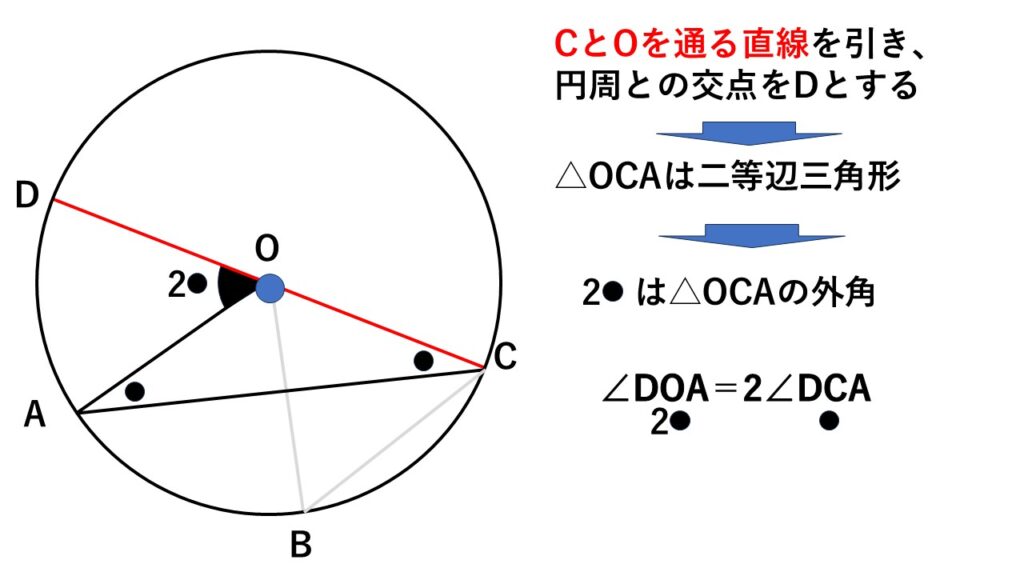
次に$\triangle OBC$に注目する
三角形の外角の性質を使うと
$\begin{align}\angle DOB&=\angle DCB+\angle OBC\\&=2\angle DCB\quad②\end{align}$

ここで①②より
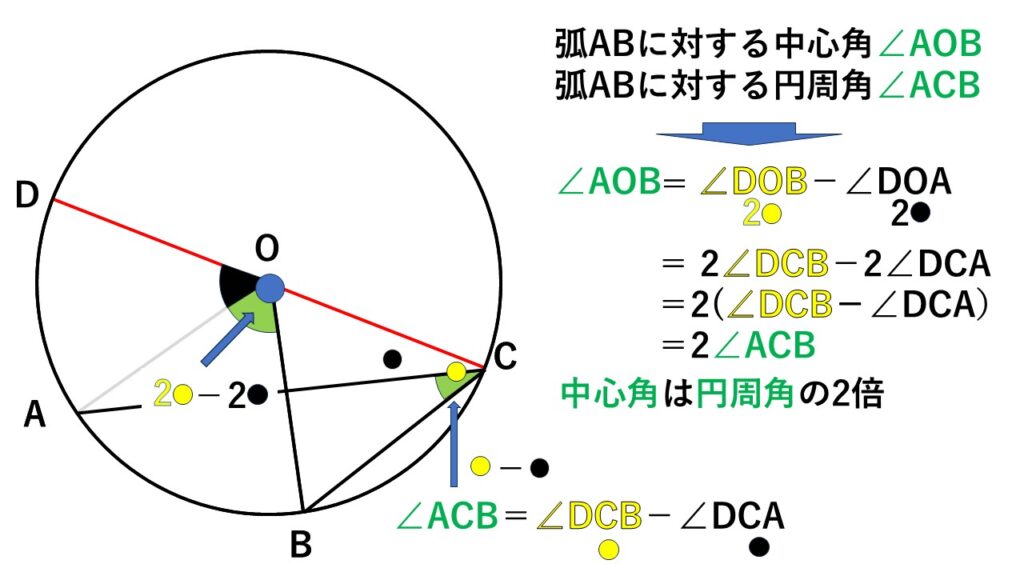
弧$AB$に対する中心角$\angle AOB$は
$\angle AOB$$\:=\:$$\angle DOB$$\:-\:$$\angle DOA$
$\begin{align}\quad\quad\quad&=2\angle DCB-2\angle DCA\\&=2(\angle DCB-\angle DCA)\\&=2\angle ACB\end{align}$

なぜ3パターンに分けて円周角の定理を証明するのか？

円周角の定理を3パターンに分けて証明しましたが、どのパターンでも弧$AB$に対する円周角と中心角を考えていることに気づいてください。
弧$AB$に対する円周角と中心角を、元々の図とは別の視点から考えるために補助線を引いています。

ではなぜ

• 円の中心が円周角の内側にある
• 円の中心が$\triangle ABC$上にある
• 円の中心が円周角の外側にある

の3パターンに分けて証明したのか？

それは計算過程がそれぞれ異なるからです。

円の中心が円周角の内側にあるときの計算過程は、2つの三角形について角の和を求めています。

円の中心が$\triangle ABC$上にあるときの計算過程も同様に2つの三角形について角の和を求めていますが、実は1つの三角形について外角の性質を使えばすぐに証明できます。
（上記の証明では半円の弧に対する円周角は$90°$になることを合わせて説明したかったため、あえて2つの三角形について考えた）

円の中心が円周角の外側にあるときの計算過程は足したり引いたり複雑で、他2つとは全く異なるものでした。

このように計算過程が異なるということは、図形的な意味が異なることを表しています。
図形的な意味が異なるということは、そのそれぞれについて証明しないと全てを証明したことにならないのです。

そのため円周角の定理の証明は、中学生にとっては難易度高めといえます。
とくに3つ目の円の中心が円周角の外側にあるときは、補助線自体なかなか気づけないかと思います。

繰り返しますが、最優先で覚えるべきは円周角の定理について。
そしてそれを使った問題を解けるようになってから、円周角の定理が成り立つ理由を理解しましょう。