三角形の相似の考えを発展させると、図形の性質についていろいろと説明できるようになります。
ここでは特に知っておきたい定理、中点連結定理について詳しく解説し、台形に応用するときの注意点についても解説します。
中点連結定理とは

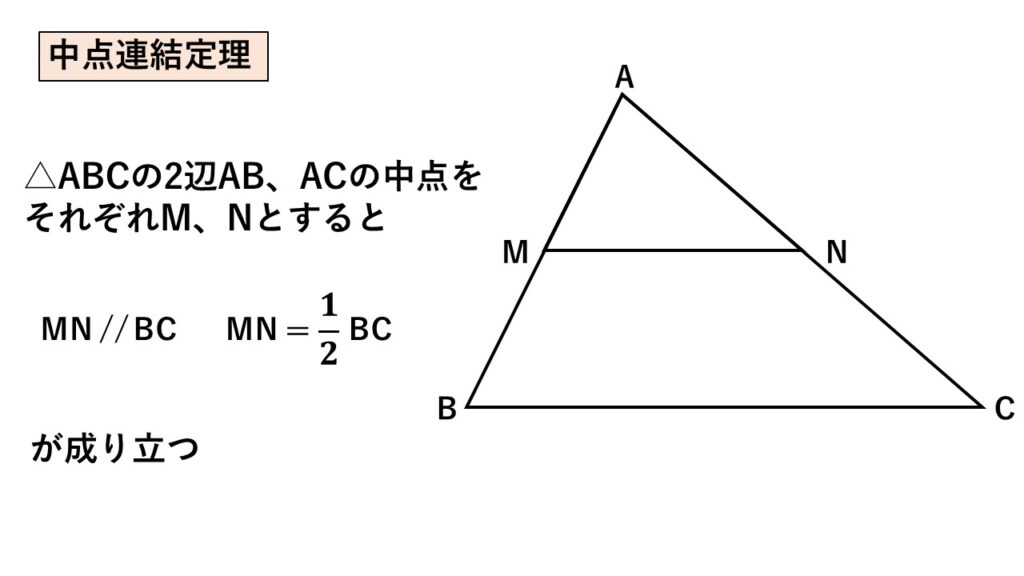
$\triangle ABC$において$AB$と$AC$の中点をそれぞれ$M,N$とすると、
$MN//BC\quad MN=\dfrac{1}{2}BC$
の関係が成り立ちます。
記号で書くと強烈な印象ですが結局のところ、
中点と中点を結んだ線は底辺に並行で、なおかつ底辺の半分の長さだ
と覚えておくと良いでしょう。
なお、前提として三角形をもとにしていることに注意は必要です。
この関係が中点連結定理の基本となります。
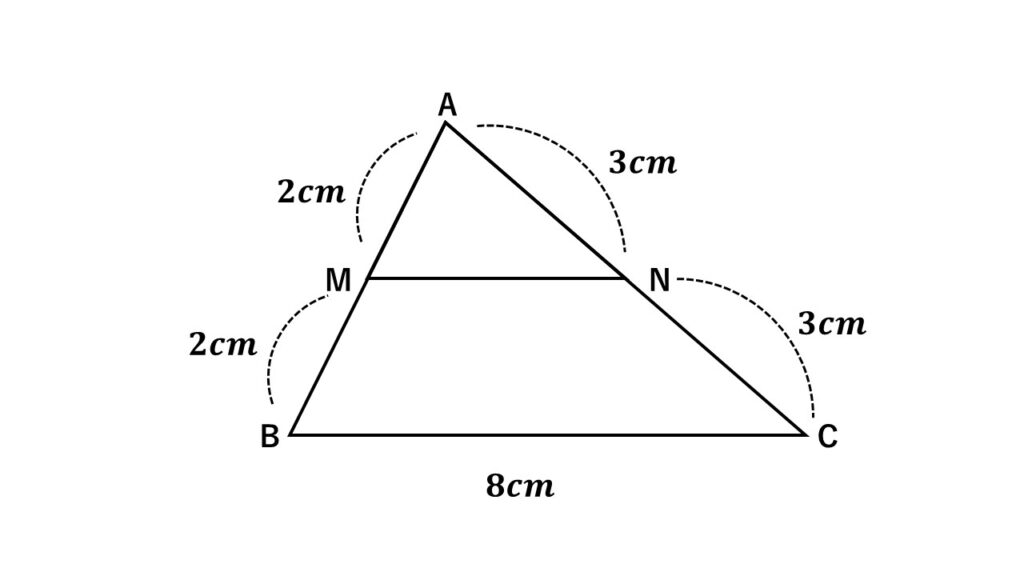
例えば$\triangle ABC$において、図のような関係があるとします。
すると中点連結定理から
$MN=4\:cm$
と一瞬で求まり、なおかつ
$MN//BC$
であることもわかります。
強調しておきますが、
中点と中点を結んでいることがはっきりしている
ときに中点連結定理が成り立ちます。
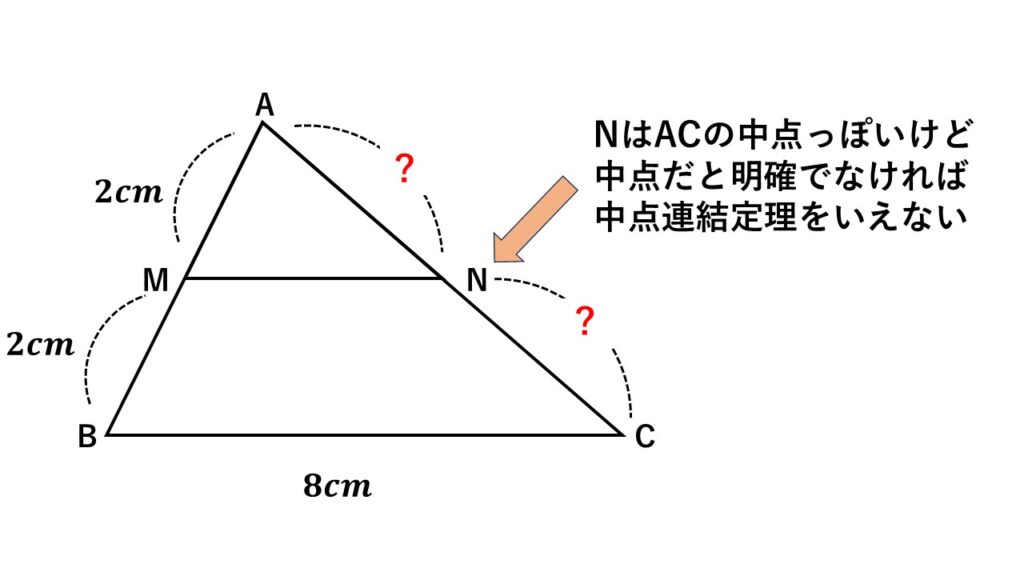
なので、一方の辺は中点だけどもう一方の辺は中点かどうかはっきりしない場合は、中点連結定理をいえません。
そのため図ように$AN$と$NC$の長さがわからないと、中点連結定理を使って考えることはできません。
つまり$MN=4cm$かどうかはわからず、$MN//BC$ともいえません。
ではどうして中点と中点を結んだときに中点連結定理が成り立つのか?
それは冒頭に書いたように三角形の相似から説明できます。
なぜ中点連結定理が成り立つのか
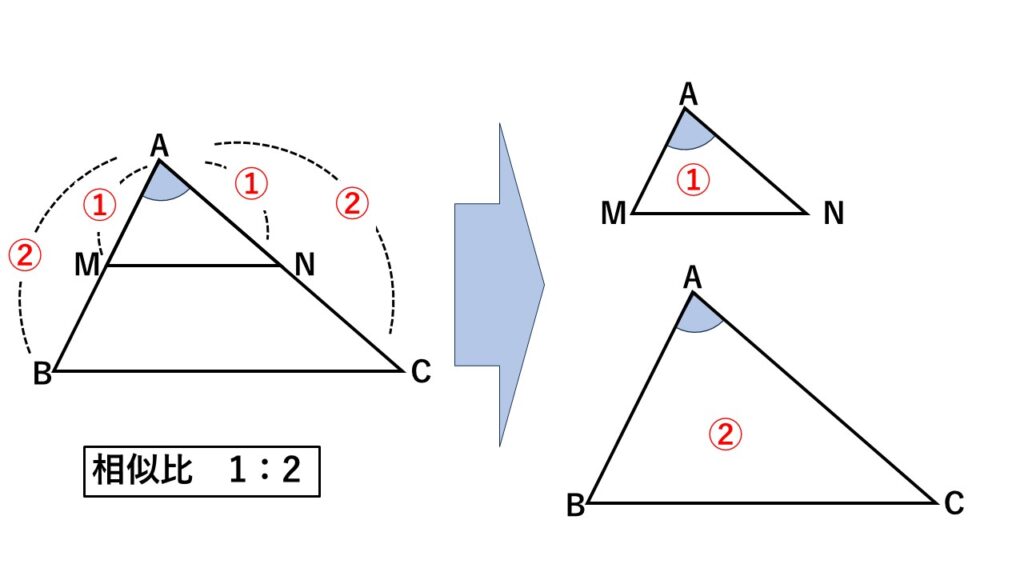
中点連結定理は図の$\triangle ABC$と$\triangle AMN$が相似であることから説明できます。
このページは相似の証明がメインではないので簡単に記します。
$\triangle AMN$と$\triangle ABC$において
$AB\quad AC$の中点がそれぞれ$M,N$より
$AM:AB=AN:AC=1:2$
また$\angle A$は共通
よって2組の辺の比とその間の角がそれぞれ等しいので
$\triangle AMN\backsim\triangle ABC$
相似比は$1:2$となるので
$MN=\dfrac{1}{2}BC$
また対応する角は等しいので
$\angle AMN=\angle ABC$
これは同位角が等しいとみなすこともできるので平行線と同位角の関係から
$MN//BC\quad$といえる
よって中点連結定理が成り立つ
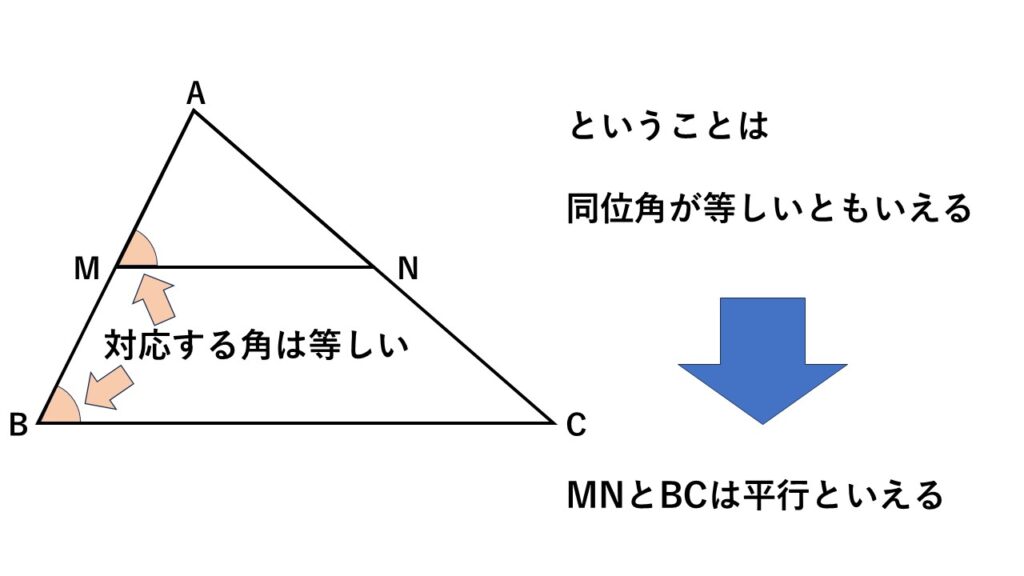
というように三角形の相似から中点連結定理を説明できます。
まずはPOINTの中点連結定理をしっかり覚えること。
それから中点連結定理が成り立つ理由を理解するようにしましょう。
それでは教科書や問題集によくある代表的な図を使って練習します。
中点連結定理の代表的な問題
基本例題1
図は$AD//BC$の台形で、$AD=4cm$、$BC=10cm$とする。
また、$EF$は$AD$と並行である。
$AB\quad DC\quad AC$の中点をそれぞれ$E\quad F\quad G$とするとき、$EG$と$GF$の長さをそれぞれ求めよ。
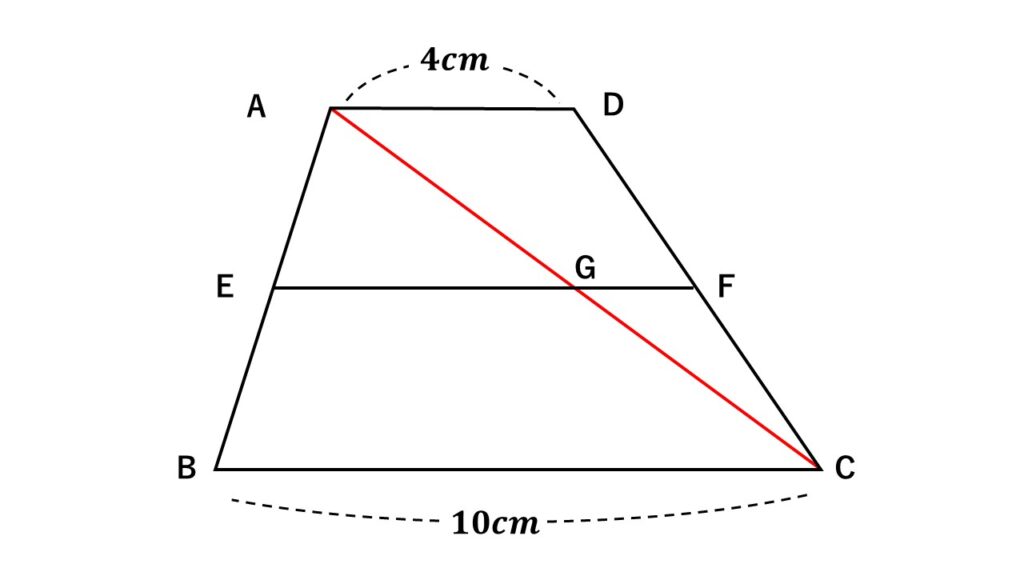
考え方
$\triangle ABC$において点$E,G$は中点です。
線分$EG$は中点と中点を結んでいるので、中点連結定理がいえます。
$\triangle CDA$についても同様に中点連結定理がいえます。
今一度強調しておきますが、
中点と中点を結んでいることがはっきりしている
ときに中点連結定理が成り立ちます。
なので、一方の辺は中点だけどもう一方の辺は中点かどうかはっきりしない場合は、中点連結定理をいえません。
本問の場合、問題文にはっきり中点と書いてあるので中点連結定理をそのまま使えます。
解答
$\triangle ABC$において中点連結定理より
$EG=5cm$
同様に
$\triangle CDA$も中点連結定理より
$GF=2cm$
解説
中点連結定理は「前提として三角形をもとにしている」と冒頭に書きました。
基本例題1では、元の図形は台形ですが対角線があることで、2つの三角形とみることができます。
そしてその三角形に対して、中点連結定理を使っています。
このように、台形に対角線を引いて三角形を作り出し中点連結定理を使う一連の流れは、比較的よく使われる考え方です。
図形問題の解き方のコツとして覚えておきましょう。
次に基本例題1に似た問題ですが、実は注意しないと誤答扱いとなってしまう、やや難易度の上がった問題を練習します。
基本例題1を理解したら次に進みましょう。
基本例題2
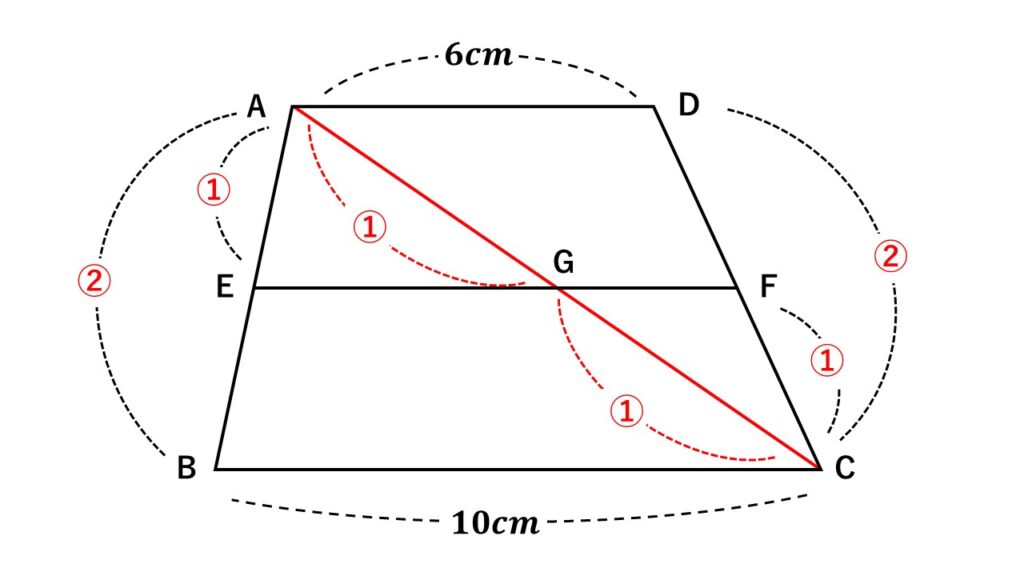
図は$AD//BC$の台形である。
$AB$の中点を$E$とし、点$E$から$AD$と平行になるように線分$EF$を引く。
$AD=6cm\quad BC=10cm$とするとき、線分$EF$の長さを求めよ。
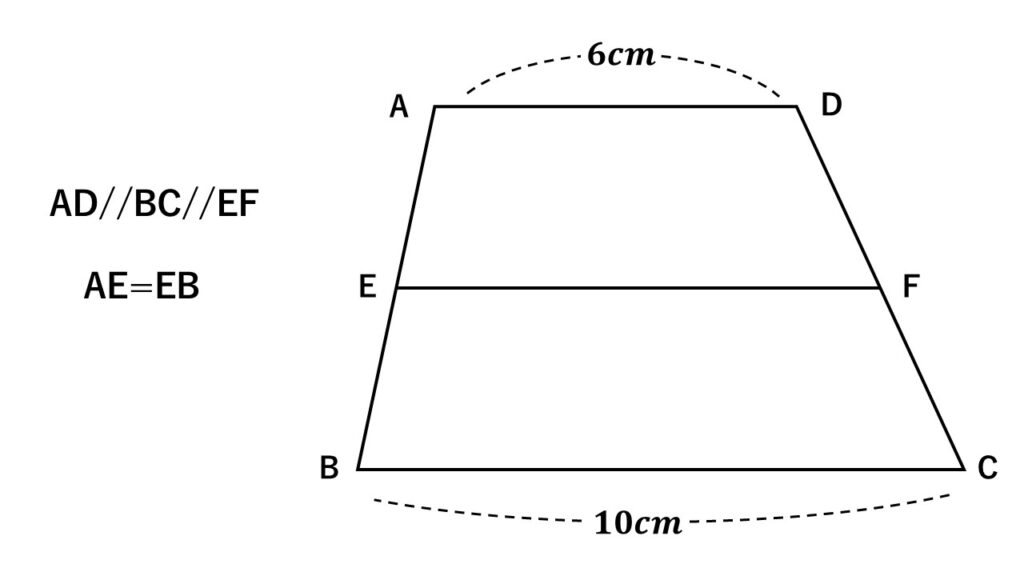
考え方
図のままでは手がかりがないので、補助線を引いて考えます。
補助線を引くコツは三角形や四角形など簡単な図形ができるようにすること。
で、ここは中点連結定理の練習なので、それを使えるような補助線を考えてみましょう。
しつこいですが強調しておきます。
中点と中点を結んでいることがはっきりしている
ときに中点連結定理が成り立ちます。
なので、一方の辺は中点だけどもう一方の辺は中点かどうかはっきりしない場合は、中点連結定理をいえません。
この問題、定期テストで問われやすい、けっこう奥が深い内容です。
解答に進む前に一通り考えてみてください。
解答(数値だけ求まれば良いとき)
対角線$AC$を引き、$EF$との交点を$G$とする。
このとき中点連結定理より
$EG=5cm$
$GF=3cm$
よって$EF=8cm$
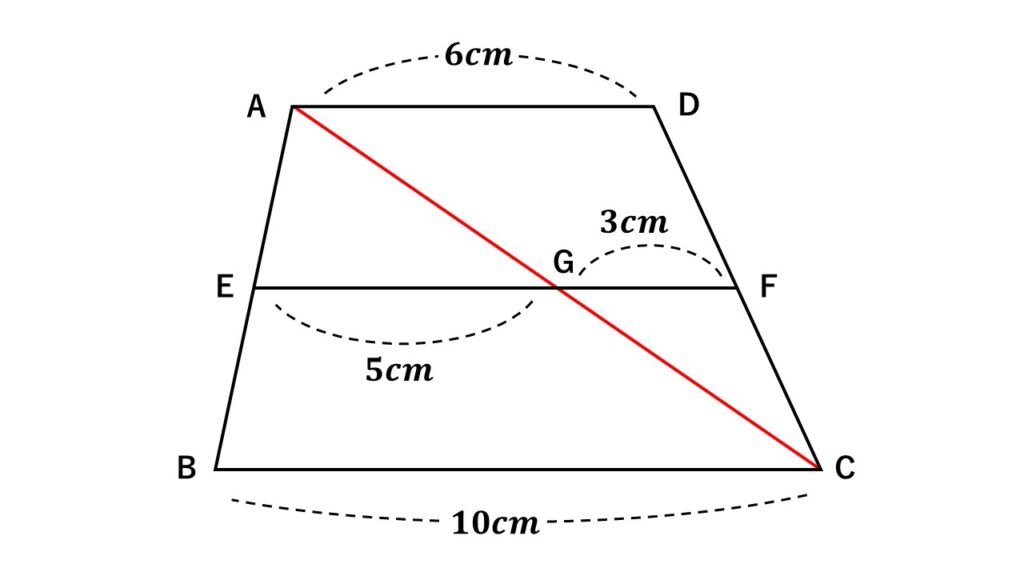
解説
対角線$AC$を引かないと中点連結定理を使えないので、これはこれで覚えてしまいましょう。
ところで解答として気になる文言(数値だけ求まれば良いとき)とありましたね。
これはどういうことかというと、
テストで$EF$の長さだけを求める出題であれば上記の解答で良いのです。
でも解答を導く過程を重視する出題だった場合、上記の解答では不十分なのです。
それが強調した
中点と中点を結んでいることがはっきりしている
というところと関わってきます。
実は単に対角線$AC$を引いただけでは、$AC$と$EF$の交点$G$が$AC$の中点だといえていないのです。(結果的に中点ではあるけども)
冒頭のPOINTの通り、中点連結定理は中点と中点を結んでいないとその性質がいえません。
そのため、$AC$と$EF$の交点$G$が$AC$の中点だとはっきり示さないといけないのです。
そこで、点$G$が$AC$の中点であることを示すために、三角形の相似を使います。

ということで、解答の過程を重視する出題のときは次のように解答します。
解答(過程を重視したもの)
対角線$AC$を引き、$EF$との交点を$G$とする
←この時点ではまだ$G$が中点とはいえていない
ここで$\triangle AEG$と$\triangle ABC$において
$\angle A$は共通 ①
$AD//EF//BC$より平行線と同位角の関係から
$\angle AEG=\angle ABC$ ②
①②より2組の角がそれぞれ等しいので
$\triangle AEG\backsim\triangle ABC$
←中点連結定理をいうための準備として
$\triangle AEG\backsim\triangle ABC$を示す
仮定より点$E$は$AB$の中点なので
$AE:EB=1:1\quad$よって
$AE:AB=1:2$
したがって
$\triangle AEG:\triangle ABC=1:2$
←相似比を示さないと長さの比の説明にならない
対応する辺の比は等しいので
$AG:AC=1:2$
これより
$AG:GC=1:1$となり
点$G$は$AC$の中点といえる
←$AG:GC=1:1$を示したことで、ようやく点$G$が$AC$の中点であることが示せた
ここで初めて中点連結定理をいうことができる
よって中点連結定理より
$EG=5cm$
同様に
$GF=3cm$
したがって
$\begin{align}EF&=EG+GF\\&=5+3=8cm\end{align}$
←さらに詳しく解答するなら$\triangle CFG\backsim\triangle CDA$を示すがそこまでする必要はない
「同様に」で通じる
図形問題は、単に定理を知っているだけでは正答にたどり着けず、理屈で考えて、長さや角度を特定できる裏付けを必要とするものも多くあります。
基本例題2の2つ目の解答はかなり理屈っぽくなっているので、少々手こずったかもしれません。
ただ1つ1つやっていること自体は決して難しいことではありません。
これまで多くの図形の性質を学んできましたが、図形問題を解く際にはその性質が本当に使えるのかを、今一度振り返ってみることも大切です。
