まず前提として、例えば
$2\div3=2\times\dfrac{1}{3}$
のように、除法(割り算)は乗法(かけ算)に直して考える様にします。
ということは、乗法の計算法則が除法にも当てはまるということになります。
かけ算で考えた方が文字式を扱う時に考えやすくなります。
そのため今後除法が出てきたら、反射的に乗法として考えるようにしてください。
乗法・除法の計算規則
同符号どうしの乗法の積は正の数
$(+2)\times(+3)=(+6)$
$(-2)\times(-3)=(+6)$ ここに注意!!
異符号どうしの乗法の積は負の数
$(-2)\times(+3)=(-6)$
$(+2)\times(-3)=(-6)$
(正の数)×(正の数)の結果が(正の数)は小学校の時から学んでいるのでわかると思います。
ではなぜ(負の数)×(負の数)の結果が(正の数)となるのか? また、異符号どうしの乗法の積は負の数になるのか? そこを説明していきます。
なぜ異符号どうしの乗法の積は(負の数)なのか?
異符号どうしの乗法の積が負の値になる理由は、次の2つの考え方で説明できます。
◆計算の流れから考える◆
例えば、
$(+2)\times(+3)=(+6)$
$(+2)\times(+2)=(+4)$
$(+2)\times(+1)=(+2)$
$(+2)\times0 =0$ ですね。
この様に、かける数を1ずつ小さくすると、かけられる数の分だけ積が小さくなっていきます。
すると、
$(+2)\times(-1)$ となった場合、積を$(+2)$としてしまうと、
$(+2)\times(+1)$ と違う計算をしているにもかかわらず同じ結果なのかよ!!
となってしまいます。
先の計算の様に、かける数が小さくなるにつれ積も小さくなっているから、
$(+2)\times(-1)$
のようにかける数が負の値でも、積が小さくならないと計算上つじつまが合わなくなってしまうのです。
なので、(正の数)×(負の数)の積を(負の数)としていきます。
「していきます」と書くと違和感があるかもしれませんが、これは数学のお約束ととらえてください。
ところで、かけ算はかける数とかけられる数を入れ替えても、計算結果は同じ(交換法則といいます)ですよね。
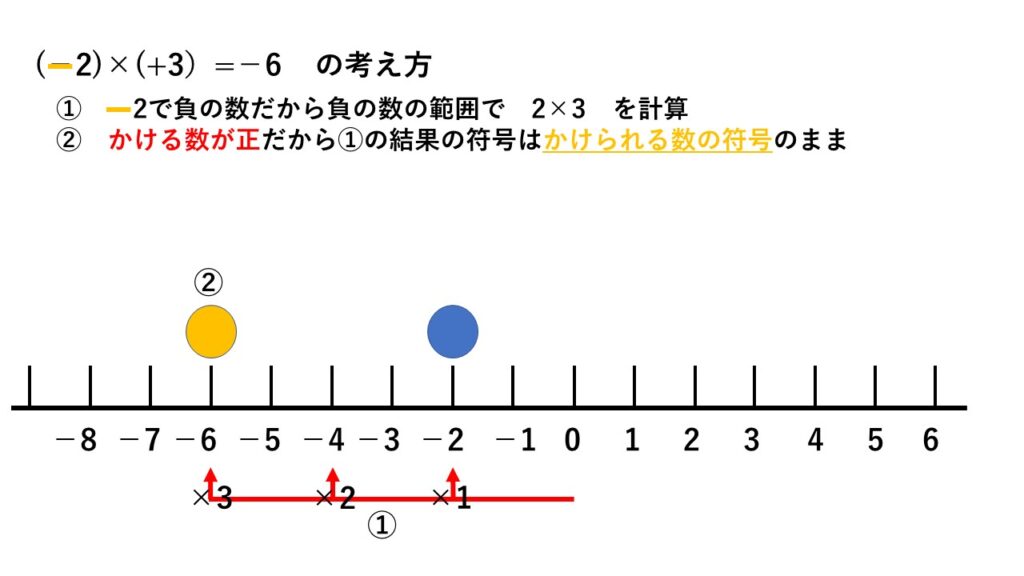
なので $(-2)\times(+1)$ のように、(負の数)×(正の数)の積も(負の数)となります。
◆マイナスの意味から考える◆
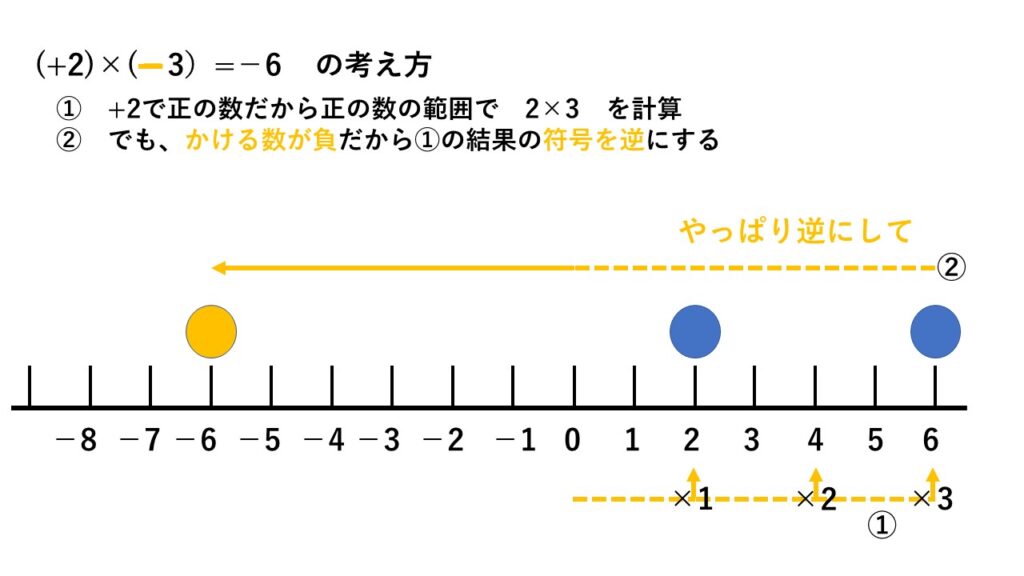
例えば $(+2)\times(-3)$ のように、かけ算記号の直後にある(かっこ)の中のマイナスは、日常的な言葉に置き換えると「やっぱり逆にして」という意味になります。
すると $(+2)\times(-3)$ の計算は、
まず $+2$ を3つ分大きくし $+6$ とします。
だけど、かけ算記号の直後の(かっこ)の中にマイナスがあるから、「やっぱり逆にして」という意味が働き「+の逆なのね」ということになります。なので結果として $-6$ となります。
なぜ(負の数)×(負の数)の積が(正の数)なのか?
$(-2)\times(-3)$ で考えます。
ここまでの内容から簡単に説明できます。
◆計算の流れから考える◆
$(-2)\times(+3)=-6$ ですよね。
$(-2)\times(+2)=-4$
$(-2)\times(+1)=-2$
$(-2)\times0=0$
かける数が1小さくなるごとに、積は2ずつ大きくなっています。
$(-2)\times(-1)$ ここで積が正の値にならないと計算のつじつまが合いません。
なので結果は$+2$となります。
したがって、
$(-2)\times(-2)=+4$
$(-2)\times(-3)=+6$ となっていきます。
◆マイナスの意味から考える◆
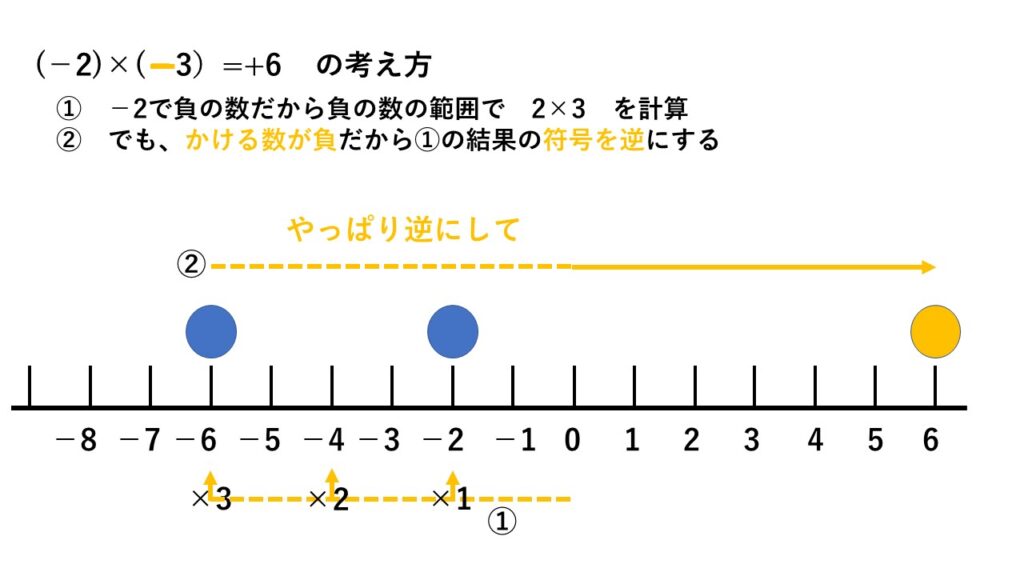

除法(わり算)は乗法(かけ算)に直して考える
同符号どうしの乗法の積は正
(+)×(+)=(+)
(−)×(−)=(+)
異符号どうしの乗法の積は負
(+)×(−)=(−)
(−)×(+)=(−)
【補足】
乗法だけの計算式のとき、
負の数が偶数個ならば計算結果は正
負の数が奇数個ならば計算結果は負
となる。
(例)
$(-1)\times(+3)\times(-2)=+6$
$(-1)\times(-3)\times(-2)=-6$
