直線とは
ここでは直線ができる条件を考えていきます。
そもそも直線とは
どこまでも続く終わりのないまっすぐ伸びた線
のことをいいます。
まずはこのことをしっかりおさえてください。
ところで「直線を引いてください」といわれたら、あなたならどんな直線を引くか?
たぶん100人に言ったら100通りの直線ができると思います。
どういうことか?
横に伸びた直線を考える人もいれば、縦に伸びた直線を考える人もいる。あるいは斜めに伸びた直線を考える人だっているはずです。
そのそれぞれについて、どの位置に直線があってどの方向に伸びていくのかを考えていくと、もう無限に直線を考えることができます。
このように、単に「直線を引いてください」と100人に言ったら100通りの直線ができてしまいます。
本当はみんな全く同じ直線を引いてくれることを期待したのに、みんなバラバラな直線を引いてしまってはちょっと困ってしまいます。
では、100人いたら100人とも同じ直線を引けるようにするにはどうすれば良いか?
ということで直線ができる条件を考えていきます。
直線ができる条件
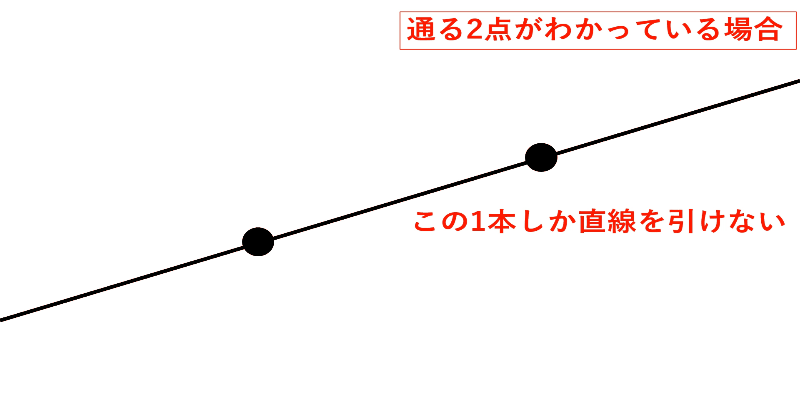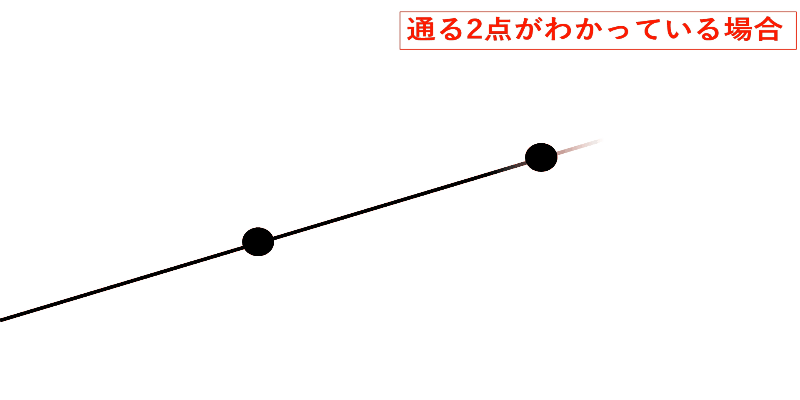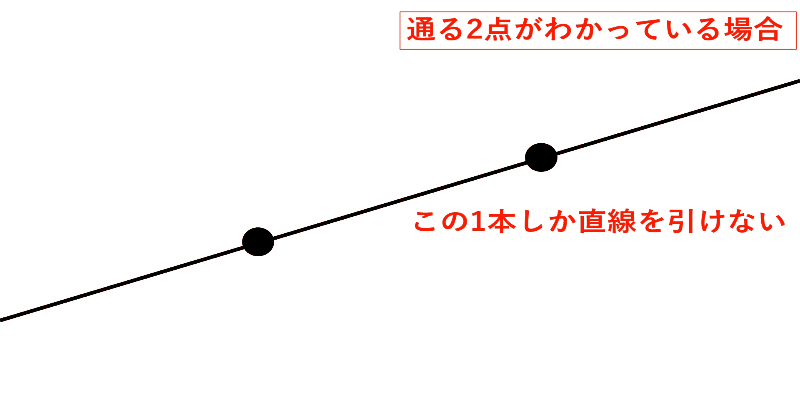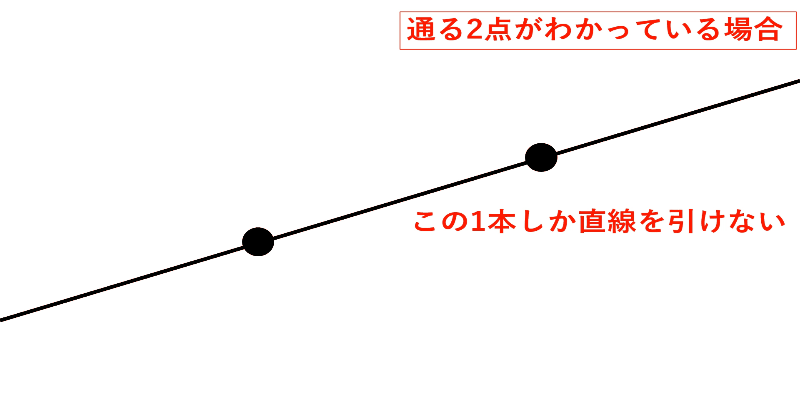
通る点が2つわかる
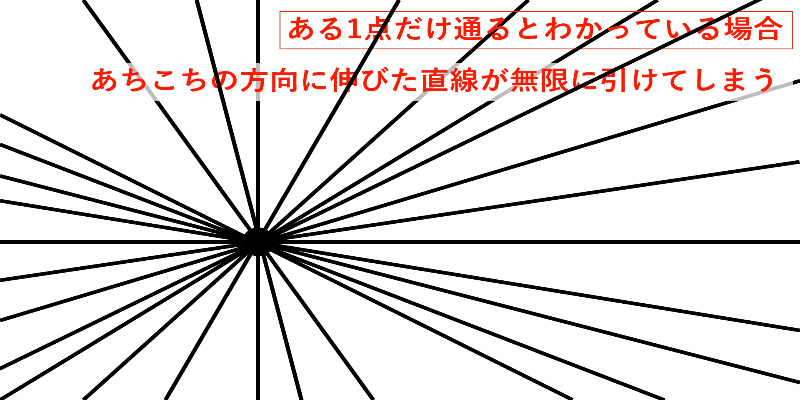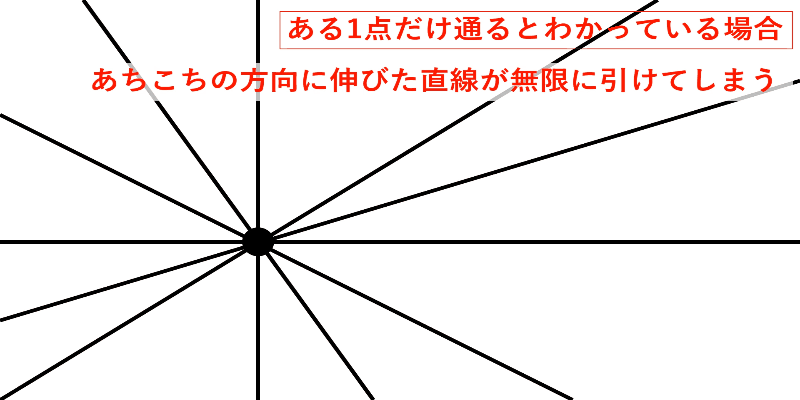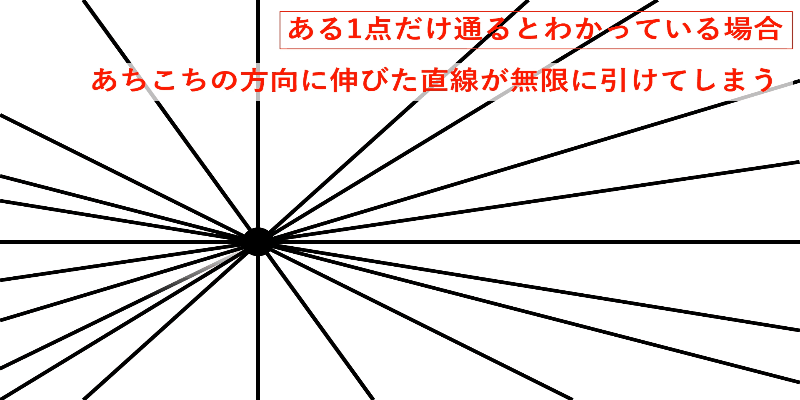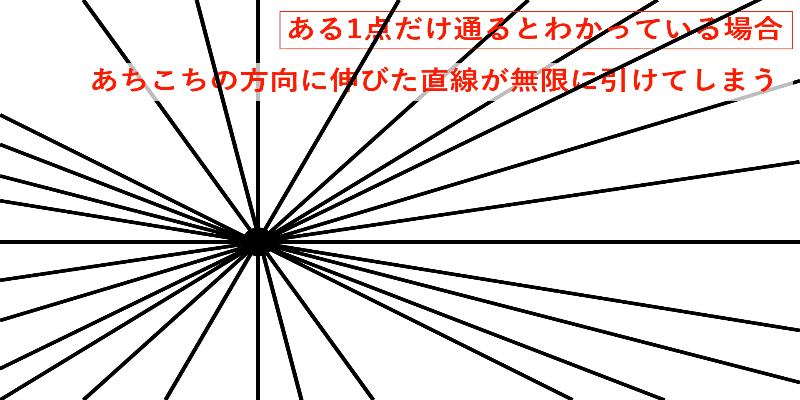
例えば、ある1点だけ通るとわかっている場合、直線は無限の本数が引けます。
でもこれではみんなが同じ直線を引くことにならないので、もう少し条件が必要です。
そこで2点を考えます。
通る点が2つわかっている場合は、線をまっすぐ伸ばしていくわけだから、引ける直線は1本に限られます。
つまりみんなが全く同じ直線を引くための条件は、通る2点がわかれば良いということになります。
これは直線を考える上で最も基本的なことなのでしっかりおさえておきましょう。
通る1点と伸びる方向がわかる
通る点が2つわかるということは見方を変えると、線を伸ばしていく方向が決まっていることにもなります。
ということは、
通る1点と直線の伸びる方向がわかれば誰でも同じ直線を引けるということになります。
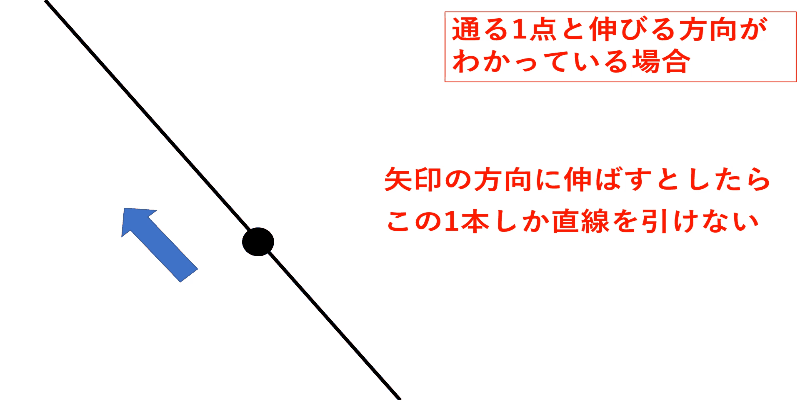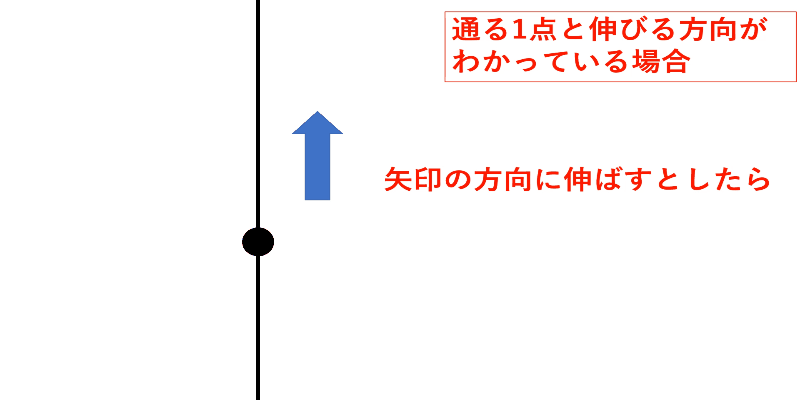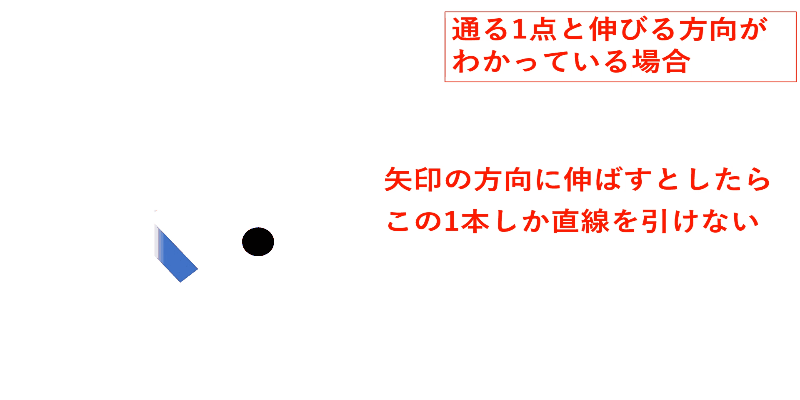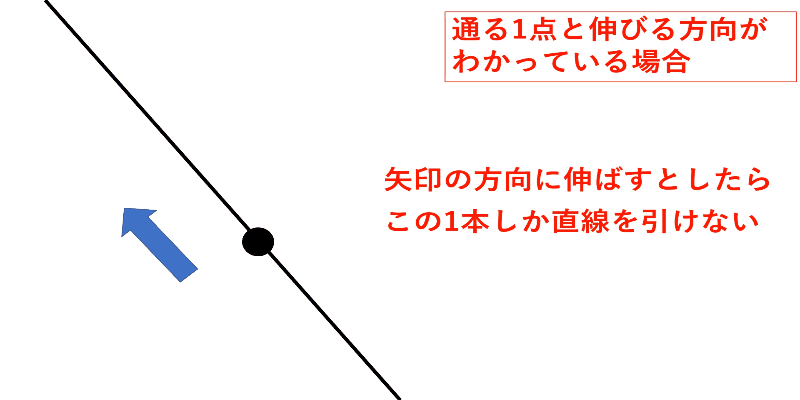
直線ができる条件は比例や一次関数の問題でよく使うので、直線がからむ問題ではこのページに書いたことを思い出してください。

直線ができる条件
・通る2点がわかる
・通る1点と直線が伸びる方向がわかる
