直角三角形の合同条件と証明問題

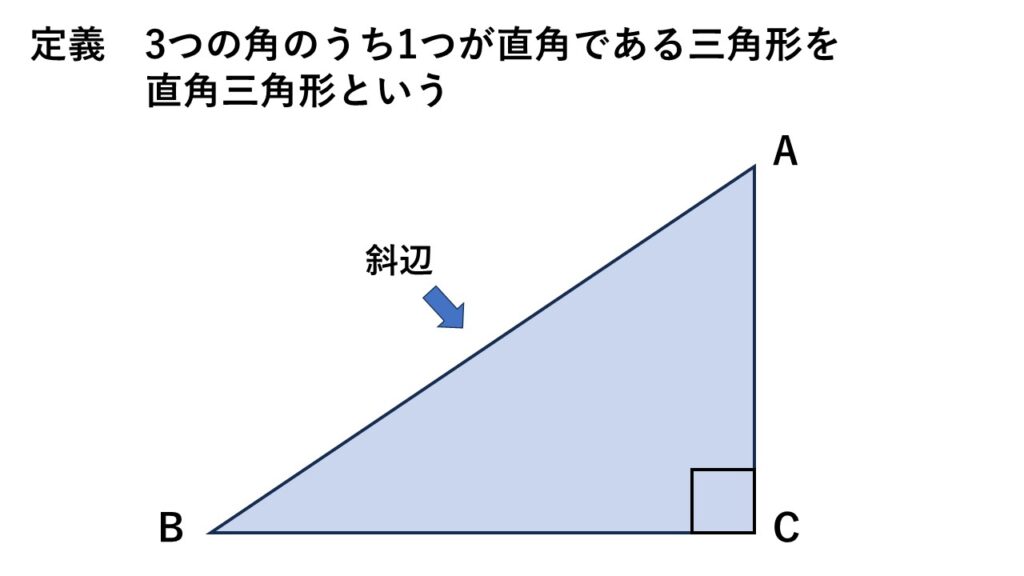
直角三角形の定義

直角三角形の定義
三角形の3つの角のうち1つが直角である三角形

上記を日常的な言葉使いに翻訳すると、
「三角形の角の中で直角（90°）になっているものがあれば、直角三角形と呼ぶことにしましょう」
となります。

直角の向かいにある辺のことを斜辺（しゃへん）といいます。3辺の中で最も長い辺です。

直角三角形の合同条件

すでに三角形の合同条件を学んでいますが、それとは別に直角三角形の場合に限って成立する合同条件があります。
これも重要なので覚えておきましょう。

例えば、2つの直角三角形がありそれぞれ合同であることを証明したい場合、上記の直角三角形の合同条件のどちらか一方をいえれば合同ということになります。
鋭角とは90°よりも小さい角のことです。

既に学んでいる三角形の合同条件は3つありましたが、直角三角形の合同を示す場合はそれらを示さなくても、直角三角形の合同条件をいえれば合同を証明したことになります。
（もちろん既に学んでいる三角形の合同条件を示しても、直角三角形の合同を証明することは可能です）

では、どうして直角三角形の合同条件が成り立つのか？
それぞれ見ていきましょう。

直角三角形の斜辺と1つの鋭角がそれぞれ等しいと合同といえる理由

直角三角形なので鋭角の大きさが1つわかれば、残りの鋭角も大きさが特定できます。
すると斜辺が等しいという前提があるので、斜辺とその両端の角、つまり「1組の辺とその両端の角がそれぞれ等しい」がいえます。
よって2つの直角三角形は合同といえます。

そのため斜辺と1つの鋭角がそれぞれ等しいと、合同な直角三角形だといえるわけです。

直角三角形の斜辺と他の1辺がそれぞれ等しいと合同といえる理由

図のような2つの直角三角形△$ABC$と△$DEF$で、$AB=DE$、$AC=DF$だとします。

この図のままでは説明が難しいので△$DEF$を反転させて、対応する$AC$と$DF$を重ねて考えます。

すると二等辺三角形を作れます。

ここで二等辺三角形の定理「底角は等しい」ことから、$∠BAC$と$∠EDF$の大きさが決まり、なおかつ同じ大きさであるとわかります。
また$AC=DF$なので、1組の辺とその両端の角がそれぞれ等しくなり、△$ABC$≡△$DEF$がいえます。

（$AB=DE$　$AC=DF$　$∠BAD=∠EDF$より、2組の辺とその間の角がそれぞれ等しいから△$ABC$≡△$DEF$もいえる）

上記解説をもとに、直角三角形の合同条件が成り立つ理由を自力で証明できるようにしましょう。
次に例題を使って、直角三角形の合同条件を使った証明の練習をします。

直角三角形の合同条件を使った証明問題

超基本例題

図のような2つの直角三角形$△ABC$と$△DEF$が合同であることを証明せよ。

考え方
証明の流れ自体は既に学んでいる三角形の合同の証明と同じです。
ここでは直角三角形なので、直角三角形の合同条件を述べるようにします。

超基本例題レベルの問題は単純すぎるため、定期テストや高校入試ではまず出題されません。
テストではふつう、他の図形と関連させた形で出題されます。
次の例題を使って証明のコツをつかんでいきましょう。

基本例題

$△ABC$で、辺$BC$の中点$M$から2辺$AB,AC$に垂線を引き、$AB,AC$との交点をそれぞれ$D,E$とする。
$MD=ME$であるとき、△$ABC$は二等辺三角形になることを証明せよ。

考え方
二等辺三角形になることを証明するので、最終的に二等辺三角形になるための条件を述べるようにします。

二等辺三角形はここで復習!!

辺に関する手がかりが少ないので、2辺が等しいことを示すのは難しそうです。
そのためここでは底角が等しいことを示して、△$ABC$が二等辺三角形であることを証明します。

ここでいう底角とは$∠ABM$と$∠ACM$。
この角を含む2つの三角形に注目し、それらが合同になることを示します。

ということで証明の手順は
①△$DBM≡△ECM$を示す
②対応する角は等しいことを示す
③底角が等しいから二等辺三角形となる
で進めます。

まずは3～4分位使って自力で証明してみましょう。

証明
△$DBM$と△$ECM$において

繰り返しますが、超基本例題のような単純な証明問題はまず出題されません。
他の図形と関連させて証明を進める問題が通常です。
そのため基本例題で挙げた証明を自力でできるようにしておきましょう。