同じ符号どうしの加法
●数直線での考え方●
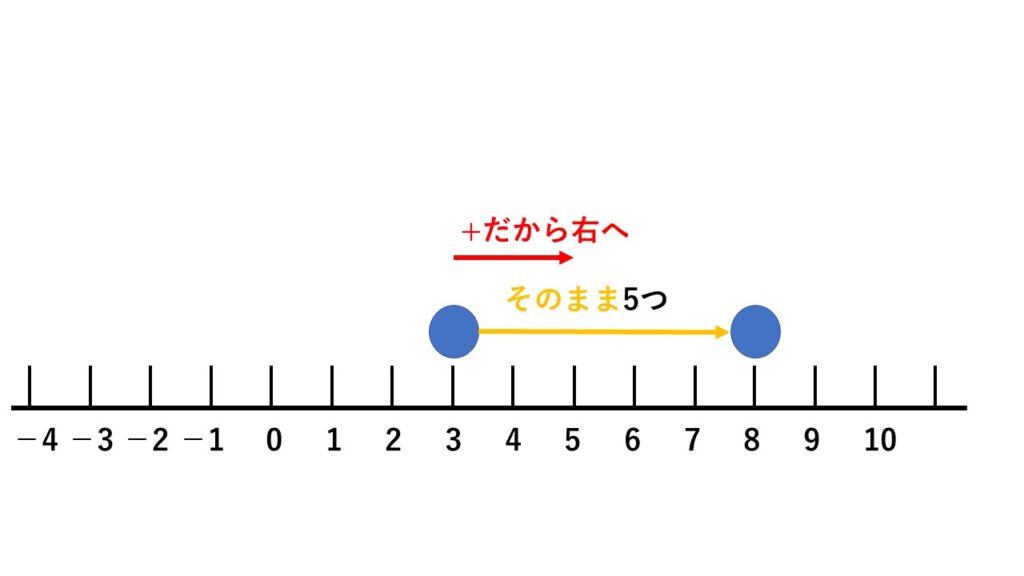
例1 (+3)+(+5)
まず(+3)からスタート。
そして、+ は「右に進め」という意味です。
どれだけ進めるのかというと、「その方向のまま5つ」。
ということで答えは(+8)となります。
例2 (−3)+(−5)
まず(−3)からスタート。
そして、+ は「右に進め」という意味です。
どれだけ進めるかというと、「やっぱり逆方向へ5つ」。
この 「やっぱり逆方向へ」 がポイント。
+(-数字) の並びの様に、(かっこ)の中にある-は、そのすぐ左隣にある符号の意味を逆にします。
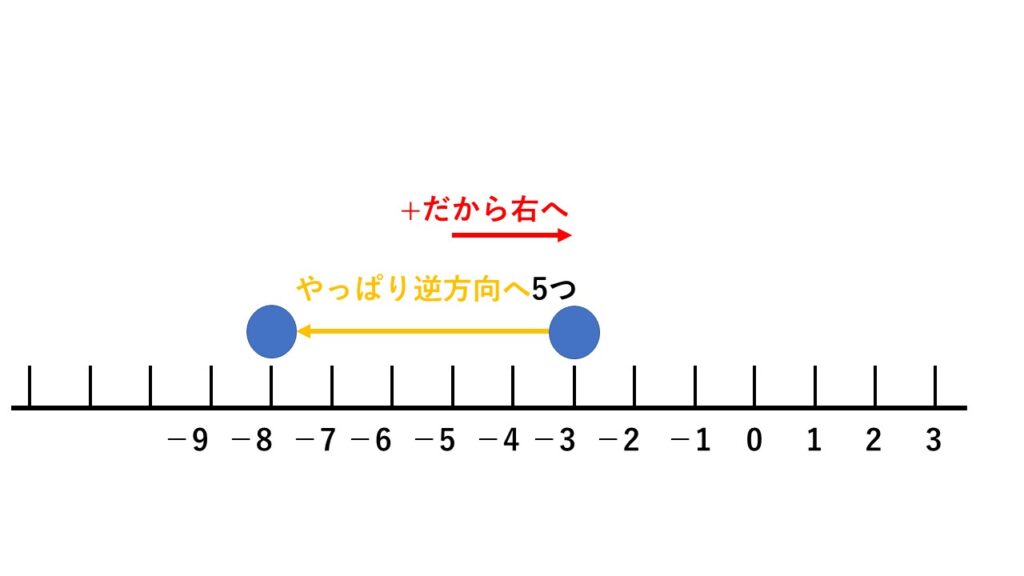
ということで、(−3)からスタートして左へ5つ進めとなり答えは(−8)となります。

(かっこ)の中にある-は、そのすぐ左隣にある符号の意味を逆にする
この考え方をしっかり覚えてください。
これは後で紹介する減法(引き算)の所でも関わってきます。
ところで、
数直線での考え方は、符号の意味を理解するために挙げています。
数直線を書くのは面倒ですよね。
それにいちいち数直線を書いていたらテストでは時間が足りなくなります。
ということで、同じ問題を使って数直線を使わない計算の仕方を示します。
実際に計算する時は、数直線を使わないで解くようにしましょう。
●同じ符号どうしの加法 計算の仕方●
①(かっこ)の外にある符号が+であることを確認
②(かっこ)の内にある符号が同じであることを確認
③絶対値(符号を無視した数値のこと)を足し算
④(かっこ)の内の同じ符号を③の結果につける
この手順で進めます。
例3 (+3)+(+5)
①(かっこ)の外にある符号は+です。
②(かっこ)の中にある符号は+と+で同じです。
③3+5を計算して8
④+8 が答え
教科書や参考書、問題集では、
(+3)+(+5)
=+(3+5)
=+8
といった書き方を見ますよね。
この書き方は2行目の所で、手順の②~④をまとめて表しています。
(+)と(+)で同じ符号だから先に+をつけておき、3と5を足し算しています。
例4 (−3)+(−5)
①(かっこ)の外にある符号は+です。
②(かっこ)の中にある符号は-と-で同じです。
③3+5を計算して8 (注意!!)
④−8 が答え
(−3)+(−5)
=-(3+5)
=-8
異符号の加法
●数直線での考え方●
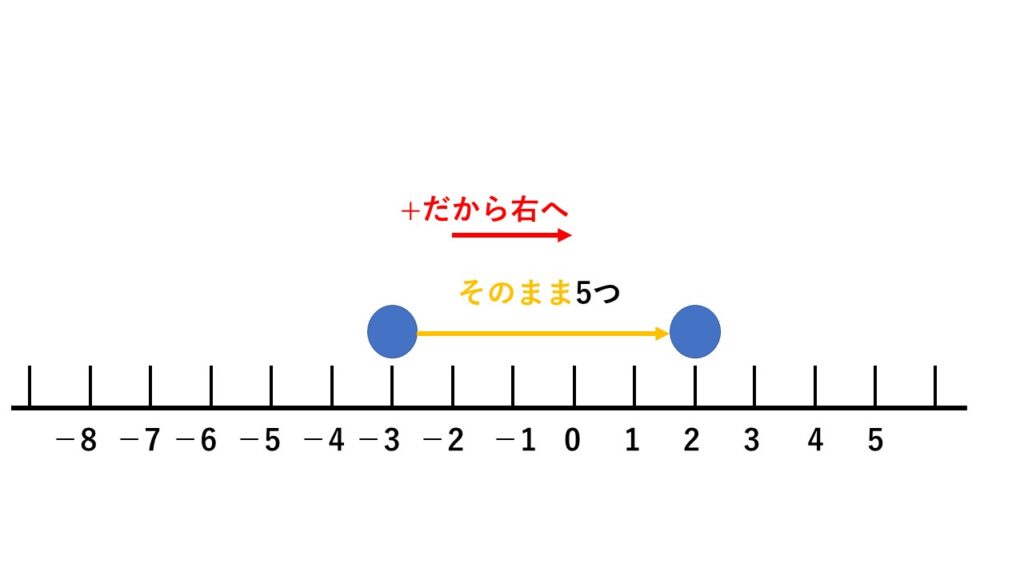
例5 (−3)+(+5)
まず(−3)からスタート。
そして、+ は「右に進め」という意味です。
どれだけ進めるのかというと、「その方向のまま5つ」。
ということで答えは(+2)となります。
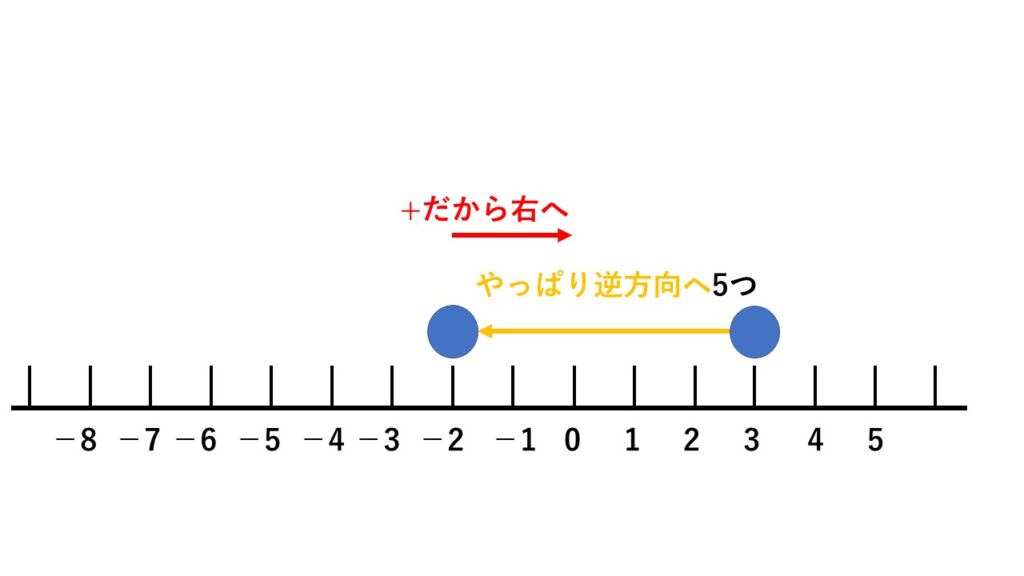
例6 (+3)+(−5)
まず(+3)からスタート。
そして、+ は「右に進め」という意味です。
どれだけ進めるのかというと、「やっぱり逆方向へ5つ」。
ということで答えは(−2)となります。
(かっこ)の中にある-が、すぐ左隣にある+の意味を逆にしています。
やはり数直線を書いていたら大変ですよね。
以下に例5、例6と同じ問題を使い数直線を使わないで解く方法を紹介します。
●異符号の加法 計算の仕方●
①(かっこ)の外にある符号が+であることを確認
②(かっこ)の中にある符号が違うことを確認
③絶対値の大きい方から絶対値の小さい方を引き算
④絶対値の大きい方の符号を③の結果につける
この手順で進めます。
例7 (−3)+(+5)
①(かっこ)の外にある符号は+です。
②(かっこ)の中にある符号は-と+で異なります。
③5-3を計算して2 (注意!!)
④+2が答え。
(−3)+(+5)
=+(5-3)
=+2
例8 (+3)+(−5)
(+3)+(−5)
=−(5-3)
=−2
多くの中学1年生が、異符号の加法計算で1度は混乱します。
なぜなら足し算なのに引き算をするから。
混乱した時は数直線を使って考えましょう。
正負の数の減法
●数直線での考え方●
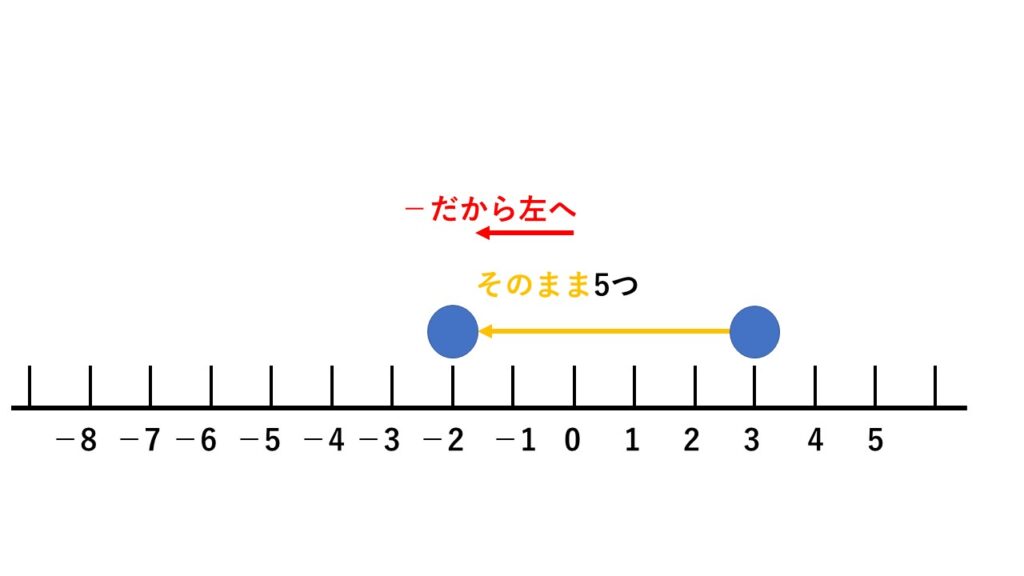
例9 (+3)−(+5)
まず(+3)からスタート。
そして、− は「左に進め」という意味です。
どれだけ進めるのかというと、「その方向のまま5つ」。
ということで答えは(−2)となります。
数直線で考えると一目瞭然ですよね。
●減法が加法になっている●
ところでこの数直線、例6で使った数直線と同じ結果になっていることに気づきましたか?
つまり、
(+3)+(−5) と同じことをやっているのです。
このように、
「減法は加法に直して考えることができる」
ということになります。
そしてこれが減法の大きなポイント。
引き算は足し算に置き換えて計算できる、ただ1つ注意点がある。
それは、
引き算記号「-」の直後にある(かっこ)の中の符号を逆にします。
正負の数の減法ではこの様に加法に直して計算を進めます。
加法に直したら、あとは上記で解説した加法の計算方法で進めるだけ。

正負の数の減法は、加法に直して計算する
この時、引き算記号の「-」の直後にある(かっこ)の中の符号を逆にする
●正負の数 減法の計算の仕方●
このポイントをふまえると、減法は次のように加法に置き換えて計算します。
(+5)-(+1) ならば(+5)+(-1)
(-1)-(+3) ならば(-1)+(-3)
(+2)-(-1) ならば(+2)+(+1)
符号を逆にすることを忘れずに。
正負の数の計算に弱点のある生徒は、この考え方があやふやになっていることが多く見られます。
しっかり確認しておきましょう。
